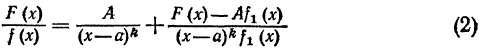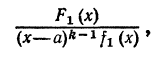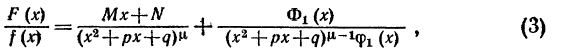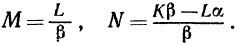Глава I

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Глава II

Глава I

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

$ 8. Разложение рациональной дроби на простейшие

       Покажем далее, что всякую правильную рациональную дробь можно разложить на сумму простейших дробей.
       Пусть нам дана правильная рациональная дробь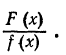
       Будем предполагать, что коэффициенты входящих в нее многочленов—действительные числа и что данная дробь несократима (последнее означает, что числитель и знаменатель не имеют общих корней).
       Т е о р е м а 1. Пусть х=а есть кореньзнаменателя кратности k, т.е. f(x)=(x-a)^kf₁(x), где f₁(а)0; тогда данную правильную дробь 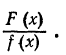можно представить в виде суммы двух правильных дробей следующим образом:

где А-постоянная, не равная нулю, а F₁(x)-многочлен, степень которого ниже знаменателя (x-a)^k-1f₁(x).
       Д о к а з а т е л ь с т в о. Напишем тождество

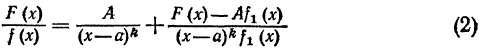
(справедливо при любом А) и определим постоянную А так, чтобы многочлен F(x)-Af₁(x) Делился на x-a. Для этого по теореме Безу необходимо и достаточно, чтобы выполнялось равенство F(a)-Af₁(a)=0. Так как f₁(a)0, F(a)0, то А однозначно определится равенством 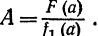При таком А будем иметь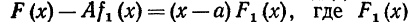, где F₁(x) есть многочлен, степень которого ниже степени многочлена (x-a)^k-1f₁(x). Сокращая дробь в формуле (2) на x-a, получаем равенство (1).
       С л е д с т в и е. К правильной рациональной дроби

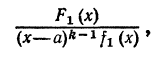
входящей в равенство (1), можно применять аналогичные рассуждения. ТАким образом, если знаменатель имеет корень x=a кратности k, то можно написать

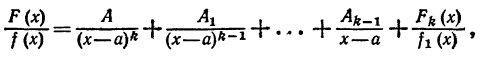
где-правильная несократимая дробь. К ней можно применить только что доказанную теорему, если f₁(x) имеет другие действительные корни.
       Рассмотрим далее случай комплексных корней знаменателя. Напомним, что комплексные корни многочлена с действительными коэффициентами всегда попарно сопряжены (см. § 8 гл. VII). В разложении многочлена на действительные множители каждой паре комплексных корней многочлена соответствует выражение вида x²+px+q. Если же комплексные корни имеют кратность , то им соответсвует выражение(x²+px+q)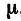
       Т е о р е м а 2. Если 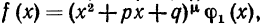, где многочлен ф₁(x) не делится на x²+px+q, то правильную рациональную дробь 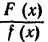можно представить в виде суммы двух других правильных дробей следующим образом:

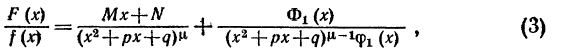
где Ф₁(x)-многочлен, степень которого ниже степени многочлена.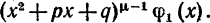
        Д о к а з а т е л ь с т в о. Напишем тождество

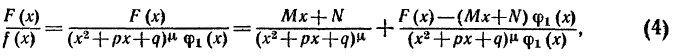
cправедливо при любых M и N, и определим M и N так, чтобы многочлен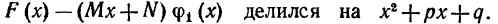Для этого необходимо и достаточно, чтобы уравнение 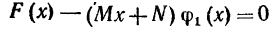имело те же корни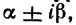что и многочлен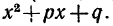Следовательно, 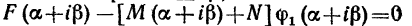или 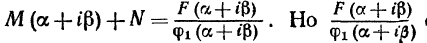есть определенное комплексное число, которое можно записать в виде K+iL, где K и L - некоторые действительные числа. Таким образом, M(a+iв)+N=K+iL; отсюда Ma+N=K, Mв=L или

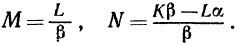
       При этих значениях коэффициентов M и N многочлен F(x) - (Mx+N)ф₁(x) имеет корнем число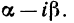 Но в таком случае многочлен без остатка разделится на разности а следовательно, и на их произведение, т.е. на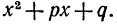 Обозначая частное от этого деления через Ф₁(x), получим

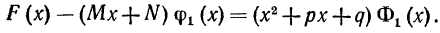
Сокращая последнюю дробь в равенстве (4) на 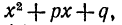получим равенство(3), причем ясно, что степень Ф₁(x) меньше степни знаменателя, что и требовалось доказать.
       Применяя теперь к правильной дроби 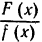результаты теорем 1 и 2, мы можем выделить последовательно все простейшие дроби, соответствующие всем корням знаменателя f(x). Таким образом, из предыдущего вытекает следующий результат.

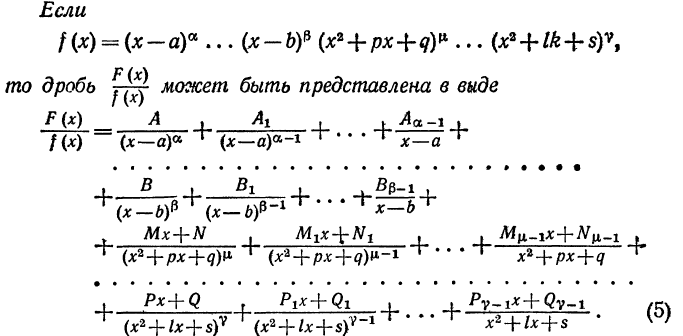
       Коэффициенты A,A₁,...,B,B₁...можно определить из следующих соображений. Написанное равенство есть тождество, поэтому, приведя дроби к общему знаменателю, получим тождесnвенные многочлены в числителях справа и слева. Приравнивая коэффициенты при одинаковых степенях х, получим систему уравнений для определения неизвестных коэффициентов A,A₁,...,B,B₁... Этот метод нахождения коэффициентов называется методом неопределенных коэффициентов.
       Наряду с этим для определения коэффициентов можно воспользоваться следующим замечанием: так как многочлены, получившиеся в правой и левой частях равенства, после приведения к общему знаменателю должны быть тождественно равны, то их значения равны при любых частных значениях х. Придавая х частные значения, получим уравнения для определения коэффициентов.
       Таким образом, мы видим, что всякая правильная рациональ- ная дробь представляется в виде суммы простейших рациональ- ных дробей.