
Электронный образовательный ресурс по теме
"Интегральные Исчисления"
"Интегральные Исчисления"
СОДЕРЖАНИЕ
Глава I
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
$ 1. Первообразная и неопределенный интеграл
$ 2. Таблица интегралов
$ 3. Некоторые свойства неопределенного интеграла
$ 4. Интегрирование методом замены переменной или способом подстановки
$ 5. Интегралы от некоторых функций, содержащих квадратный трехчлен
$ 6. Интегрирование по частям
$ 7. Рациональные дроби. Простейшие рациональные дроби и их интегрирование
$ 8. Разложение рациональной дроби на простейшие
$ 9. Интегрирование рациональных дробей
$ 10. Интегралы от иррациональных функций
$ 11. Интегрирование некоторых классов тригонометрических функций
$ 1. Постановка задачи. Нижняя и верхняя интегральные суммы
$ 2. Определенный интеграл. Теорема о существовании определенного
интеграла
$ 3. Основные свойства определенного интеграла
$ 4. Вычисление определенного интеграла. Формула Ньютона — Лейбница
$ 5. Замена переменной в определенном интеграле
$ 6. Интегрирование по частям
$ 7. Несобственные интегралы
$ 8. Приближенное вычисление определенных интегралов
$ 9. Формула Чебышева
$ 10. Интегралы, зависящие от параметра. Гамма-функция
$ 11. Интегрирование комплексной функции действительной переменной
$ 12. Геометрические и механические приложения определенного интеграла
$ 1. Определение двойного интеграла
$ 2. Замена переменных в двойном интеграле
$ 3. Приложения двойного интеграла.
$ 4. Тройной интеграл.
$ 1. Определение криволинейного интеграла второго рода
$ 2. Интеграл по замкнутому контуру
$ 3. Условия независимости интеграла от пути интегрирования.
$ 1. Поверхностные интегралы первого и второго рода.
$ 2. Формула Стокса.
$ 3. Формула Остроградского.
Глава I
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
$ 9. Интегрирование рациональных дробей
Пусть требуется вычислить интеграл от рациональной дроби 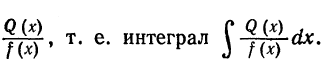
Если данная дробь н е п р а в и л ь н а я, то мы представляем ее в виде суммы многочлена М(х) и п р а в и л ь н о й рациональной дроби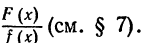 Последнюю же представляем по формуле(5) § 8 в виде суммы п р о с т е й ш и х дробей. Таким образом, интегрирование всякой рациональной дроби сводится к интегрированию многочлена и нескольких п р о с т е й ш и х дробей.
Последнюю же представляем по формуле(5) § 8 в виде суммы п р о с т е й ш и х дробей. Таким образом, интегрирование всякой рациональной дроби сводится к интегрированию многочлена и нескольких п р о с т е й ш и х дробей.
Из результатов § 8 следует, что вид простейших дробей определяется корнями знаменателя f(x). Здесь возможны следующие случаи.
1 с л у ч а й. Корни знаменателя действительны и различны, т.е
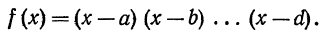
В этом случае дробь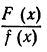 разлагается на простейшие дроби 1 типа:
разлагается на простейшие дроби 1 типа:
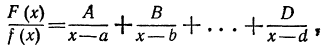
и тогда
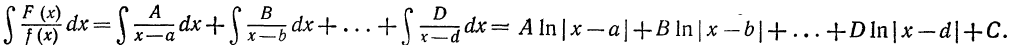
2 с л у ч а й. Корни знаменателя действительные, причем некоторые из них кратные
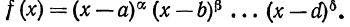
В этом случае дробь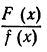 разлагается на простейшие дроби 1 и 2 типов.
разлагается на простейшие дроби 1 и 2 типов.
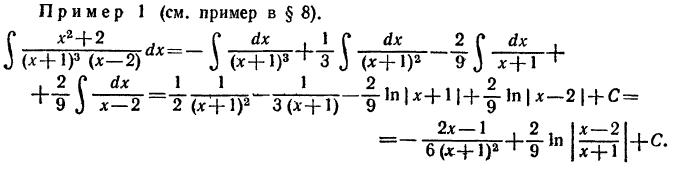
3 с л у ч а й. Среди корней знаменателя есть комплексные неповторяющиеся(т.е. различные):
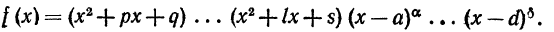
В этом случае дробь 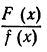 разлагается на простейшие дроби 1, 2 и 3 типов.
разлагается на простейшие дроби 1, 2 и 3 типов.

4 с л у ч а й. Среди корней знаменателя есть комплексные кратные:
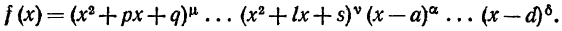
В этом случае разложение дроби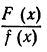 будет содержать и простейшие дроби 4 типа.
будет содержать и простейшие дроби 4 типа.
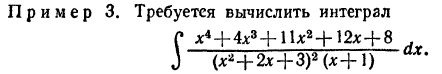

Из всего изложенного следует, что интеграл от любой рациональной функции может быть выравнен через элементарные функции в конечном виде, а именно:
1) через логарифмы —в случае простейших дробей I типа;
2) через рациональные функции — в случае простейших дробей
II типа;
3) через логарифмы и арктангенсы —в случае простейших дробей III типа;
4) через рациональные функции и арктангенсы—в случае
простейших дробей IV типа.
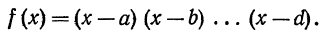
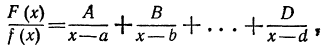
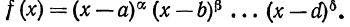
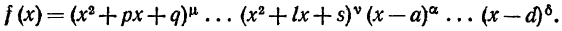
В этом случае разложение дроби
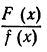 будет содержать и простейшие дроби 4 типа.
будет содержать и простейшие дроби 4 типа.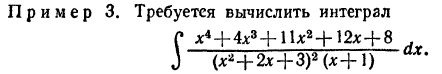

Из всего изложенного следует, что интеграл от любой рациональной функции может быть выравнен через элементарные функции в конечном виде, а именно:
1) через логарифмы —в случае простейших дробей I типа;
2) через рациональные функции — в случае простейших дробей II типа;
3) через логарифмы и арктангенсы —в случае простейших дробей III типа;
4) через рациональные функции и арктангенсы—в случае простейших дробей IV типа.