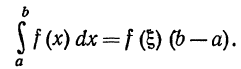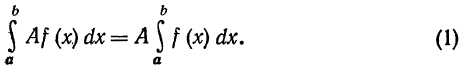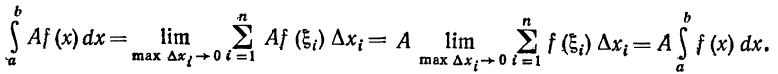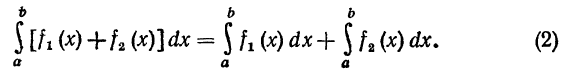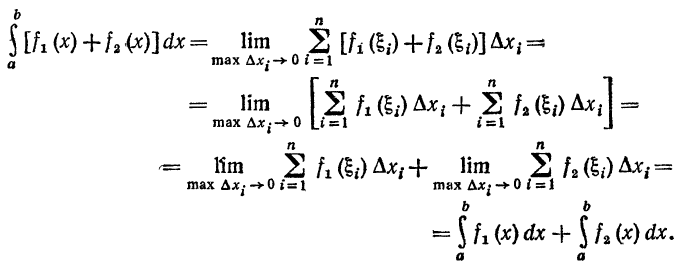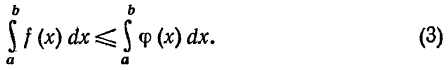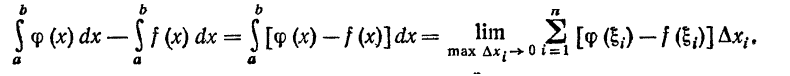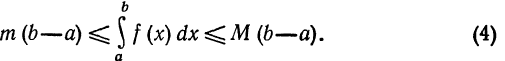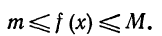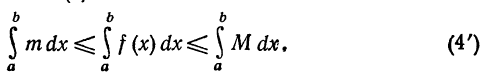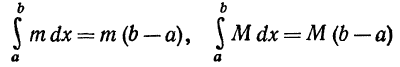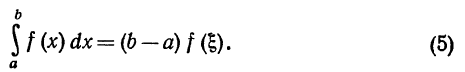Электронный образовательный ресурс по теме
"Интегральные Исчисления"
"Интегральные Исчисления"
СОДЕРЖАНИЕ
Глава I
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
$ 1. Первообразная и неопределенный интеграл
$ 2. Таблица интегралов
$ 3. Некоторые свойства неопределенного интеграла
$ 4. Интегрирование методом замены переменной или способом подстановки
$ 5. Интегралы от некоторых функций, содержащих квадратный трехчлен
$ 6. Интегрирование по частям
$ 7. Рациональные дроби. Простейшие рациональные дроби и их интегрирование
$ 8. Разложение рациональной дроби на простейшие
$ 9. Интегрирование рациональных дробей
$ 10. Интегралы от иррациональных функций
$ 11. Интегрирование некоторых классов тригонометрических функций
$ 1. Постановка задачи. Нижняя и верхняя интегральные суммы
$ 2. Определенный интеграл. Теорема о существовании определенного
интеграла
$ 3. Основные свойства определенного интеграла
$ 4. Вычисление определенного интеграла. Формула Ньютона — Лейбница
$ 5. Замена переменной в определенном интеграле
$ 6. Интегрирование по частям
$ 7. Несобственные интегралы
$ 8. Приближенное вычисление определенных интегралов
$ 9. Формула Чебышева
$ 10. Интегралы, зависящие от параметра. Гамма-функция
$ 11. Интегрирование комплексной функции действительной переменной
$ 12. Геометрические и механические приложения определенного интеграла
$ 1. Определение двойного интеграла
$ 2. Замена переменных в двойном интеграле
$ 3. Приложения двойного интеграла.
$ 4. Тройной интеграл.
$ 1. Определение криволинейного интеграла второго рода
$ 2. Интеграл по замкнутому контуру
$ 3. Условия независимости интеграла от пути интегрирования.
$ 1. Поверхностные интегралы первого и второго рода.
$ 2. Формула Стокса.
$ 3. Формула Остроградского.
Глава II
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
$ 3. Основные свойства определенного интеграла
С в о й с т в о 1. Постоянный множитель можно не выносить за знак определенного интеграла: если А = const, то
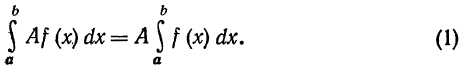
Д о к а з а т е л ь с т в о.
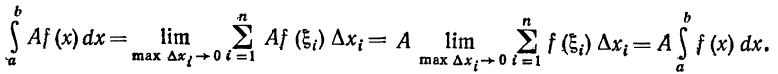
С в о й с т в о 2. Определенный интеграл от алгебраической суммы нескольких функций равен алгебраической сумме интегралов от слагаемых. Так, в случае двух слагаемых
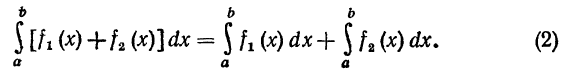
Д о к а з а т е л ь с т в о.
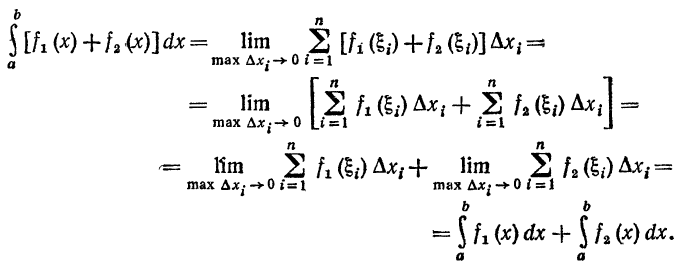
Доказательство проводится аналогично для любого числа слагаемых.
Свойство 1 и 2, хотя и доказаны только для случая a < b, остаются в силе и при 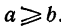
Однако следующее свойство справедливо при a < b:
С в о й с т в о 3. Если на отрезке [a,b], где a < b, функции f(x) и ф(х) удовлетворяют условию 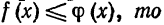
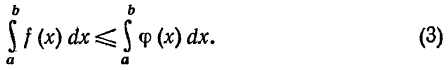
Д о к а з а т е л ь с т в о. Рассмотрим разность
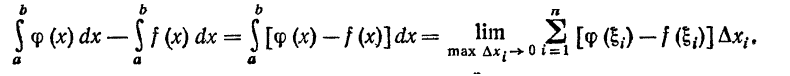
Здесь каждая разность 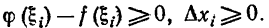 Следовательно, каждое слагаемое суммы неотрицательно, неотрицательна вся сумма и неотрицателен ее предел, т.е.
Следовательно, каждое слагаемое суммы неотрицательно, неотрицательна вся сумма и неотрицателен ее предел, т.е. 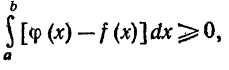 или
или 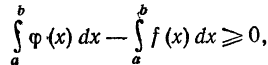 откуда следует неравенство (3).
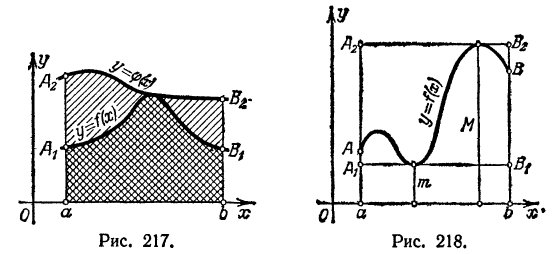
Если f(x)>0 и ф(х)>0, то указанное свойство наглядно иллюстрируется геометрически (рис. 217). Так как
откуда следует неравенство (3).
Если f(x)>0 и ф(х)>0, то указанное свойство наглядно иллюстрируется геометрически (рис. 217). Так как  то площадь криволинейной трапеции aA1B1b не больше площади криволинейной трипеции aA2B2b.
то площадь криволинейной трапеции aA1B1b не больше площади криволинейной трипеции aA2B2b.
С в о й с т в о 4.Если m и М - наименьшее и наибольшее значения функции f(x) на отрезке [a,b] и а < b, то
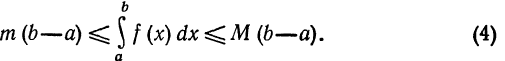
Д о к а з а т е л ь с т в о. По условию
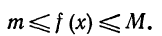
На основании свойства (3) имеем
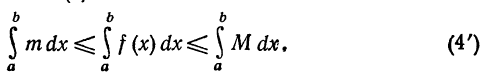
Но
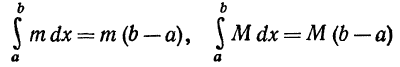
(см пример 3 § 2). Подставляя эти выражения в неравенство (4'), получим неравенство (4).
Если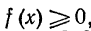 то это свойство легко иллюстрируется геометрически(рис. 218): площадь криволинейной трапеции aA1B1b и aA2B2b.
то это свойство легко иллюстрируется геометрически(рис. 218): площадь криволинейной трапеции aA1B1b и aA2B2b.
С в о й с т в о 5 (теорема о среднем).Если функция f(x) непрерывна на отрезке [a,b], то на этом отрезке найдется такая точка 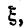 что справедливо следующее равенство:
что справедливо следующее равенство:
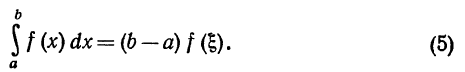
Д о к а з а т е л ь с т в о. Пусть для определенности a < b. Если m и M суть соответственно наименьшее и наибольшее значения f(x) на отрезке [a,b], то в силу формулы (4)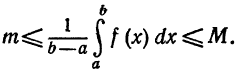
Отсюда 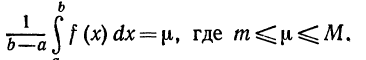
Так как f(x) непрерывна на отрезке [a,b], то она принимает все промежуточные значения, заключенные между m и M. Следовательно, при некотором значении 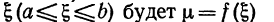 , т.е.
, т.е.