Глава I

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Глава II

Глава I

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

$ 4. Интегрирование методом замены переменной или способом подстановки

Пусть требуется найти итеграл 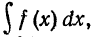причем непосредственно подобрать первообразную для f(x) мы не можем, но нам известно, что она существует.

Сделаем замену переменной в подынтегральном выражении, положив

где ф(t) - непрерывная функция с непрерывной производной, имеющая обратную функцию. Тогда 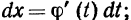докажем, что в этом случае имеет место следующее равенство:

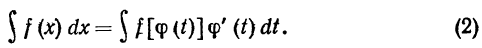
Здесь подразумевается, что после интегрирования в правой части равенства вместо t будет подставлено его выражение через х на основании равенства (1).

   Для того чтобы установить, что выражения, стоящие справа и слева, одинаковы в указанном выше смысле, нужно доказать, что их производные по х р-авны между собой. Находим производную от левой части: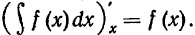 Правую часть равенства (2) будем дифференцировать по х как сложную функцию, где t — промежуточный аргумент. Зависимость t от х выражается равенством (1), при этом 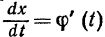и по правилу дифференцирования обратной функции 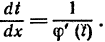Таким образом, имеем:

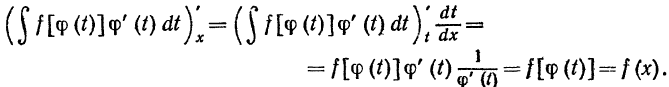
Следовательно, производные по х от правой и левой частей равен- ства (2) равны, что и требовалось доказать. Функцию х = ф(t) следует выбирать так, чтобы можно было вычислить неопределенный интеграл, стоящий в правой части равенства (2).

   Замечание.При интегрировании иногда целесообразнее подбирать замену переменной не в виде х = ф(t), а в виде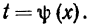

Проиллюстрируем это на примере. Пусть нужно вычислять интеграл, имеющий вид

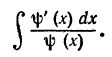
Здесь удобно положить

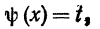
   Приведем несколько примеров на интегрирование с помощью замены переменных.

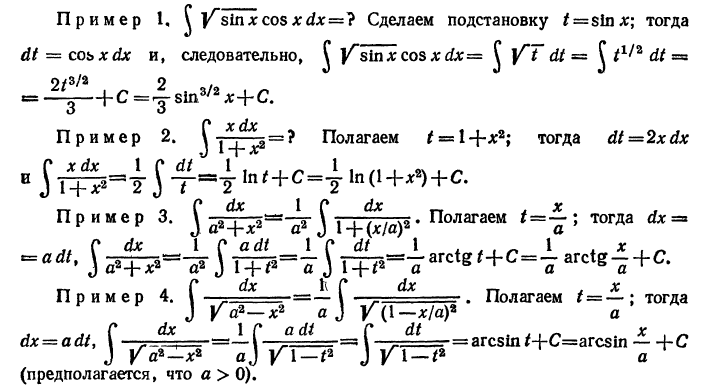
   В примерах 3 и 4 выведены формулы, приведенные в таблице интегралов под номерами 11' и 13'(см выше § 2).

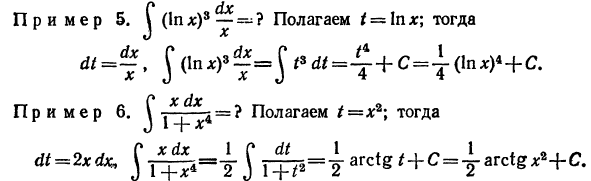
   Методы замены переменных является одним из основных методов вычисления неопределенных интегралов. Даже в тех случаях, когда мы интегрируем каким-либо другим методом, нам часто приходится в промежуточных вычислениях прибегать к замене переменных. Успех интегрирования зависит в значительной степени от того, сумеем ли мы подобрать такую удачную замену переменных, которая упростила бы данный интеграл. По существу говоря, изучение методов интегрирования сводится к выяснению того, какую надо сделать замену переменной при том или ином виде подынтегрального выражения. Этому и посвящена большая часть настоящей главы.