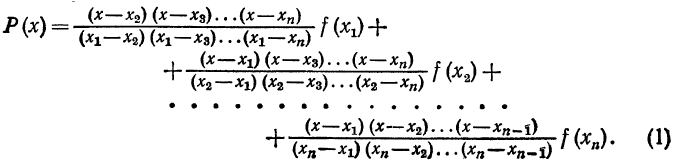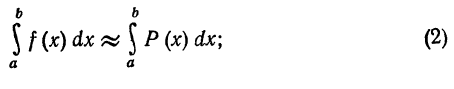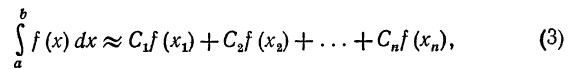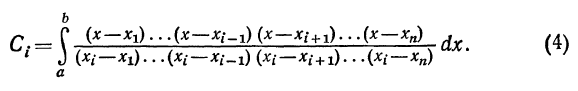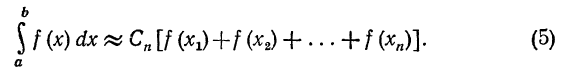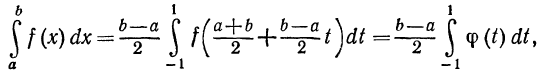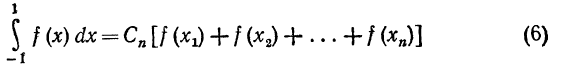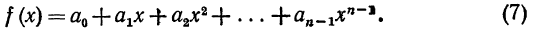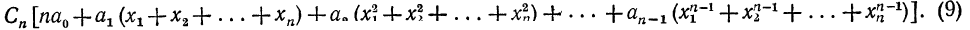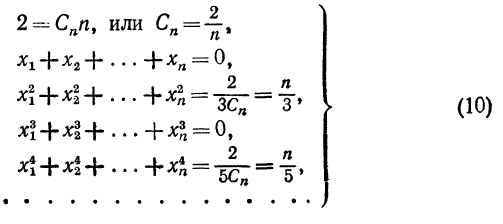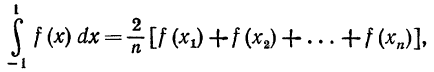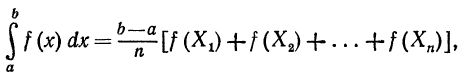Глава I

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Глава II

Глава II

ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

$ 9. Формула Чебышева

       В технических вычислениях часто применяется формула Чебышева для приближенного интегрирования.
Пусть снова требуется вычислить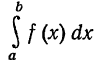
Заменим подынтегральную функцию интерполяционным многочленом Лагранжа Р (х), взяв на отрезке [а, b] некоторые n значений функции 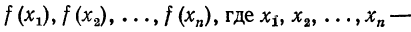какие угодно точки отрезка [a,b]:

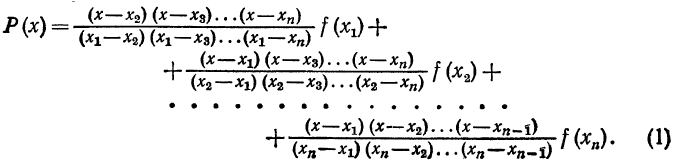
Получим следующую приближенную формулу интегрирования:

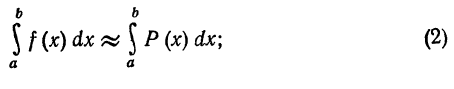
после некоторых вычислений она примет вид

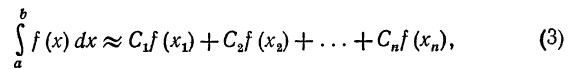
где коэффициенты Ci вычисляются по формулам

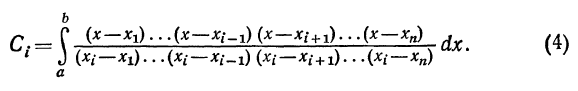
Формула (З) громоздка и неудобна для вычислений, так как коэффициенты С_i выражаются сложными дробями.
Чебышев поставил обратную задачу: задать не абсциссы x1,x2,x3,...,x_n, a коэффициенты 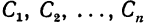и определить абсциссы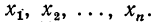
Коэффициенты C_i - задаются так, чтобы формула (3) была возможно проще для вычислений. Очевидно, что это будет тогда, когда все коэффициенты C_i равны между собой: С1 = С2 = ... = C_n.
Если обозначить общее значение коэффициентов C1, С2, ..., C_n через C_n то формула (3) примет вид

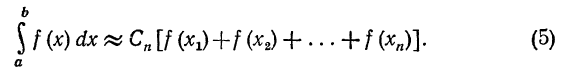
Формула (5) представляет вообще приближенное равенство, но если f(x) есть многочлен степени не выше n — 1, то равенство будет точным. Это обстоятельство и позволяет определить вели- чины C_n ,х1,х2, ..., x_n.
Чтобы получить формулу, удобную для любого промежутка интегрирования, преобразуем отрезок интегрирования [а, b] в отре- зок [—1, 1]. Для этого положим 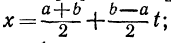тогда при t=-1 будет х=а, при t=1 будет x=b.
Следовательно,

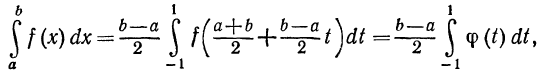
где через ф (t) обозначена функция от t, стоящая под знаком интеграла. Таким образом, задача интегрирования данной функции f(x) на отрезке [а, b] всегда может быть сведена к интегрирова- нию некоторой другой функции ф(х) на отрезке [—1, 1].
Итак, задача свелась к тому, чтобы в формуле

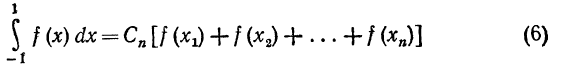
подобрать числа C_n ,х1,х2, ..., x_n так, чтобы эта формула была точной для всякой функции f(x) вида

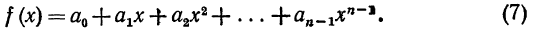
Заметим, что

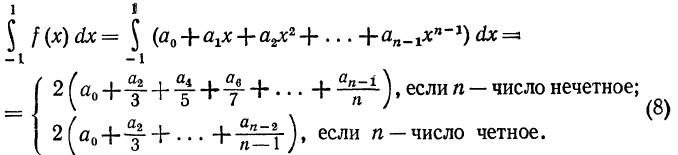
С другой стороны, сумма, стоящая в правой части равенства (6), на основании (7) будет равна

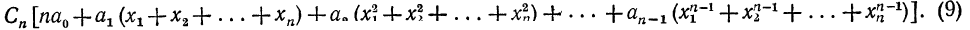
Приравнивая выражения (8) и (9), получим равенство, которое должно быть справедливо при любых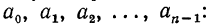

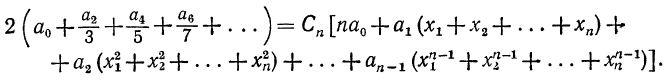
Приравниваем коэффициенты при 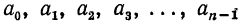в левой и правой частях равенства:

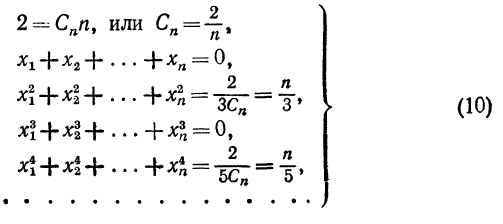
Из последних п — 1 уравнений находим абсциссы x1,x2,x3,...,x_n. Эти решения найдены Чебышевым для различных значений n. Ниже приводятся найденные им решения в случаях, когда число n промежуточных точек равно 3, 4, 5, 6, 7, 9:

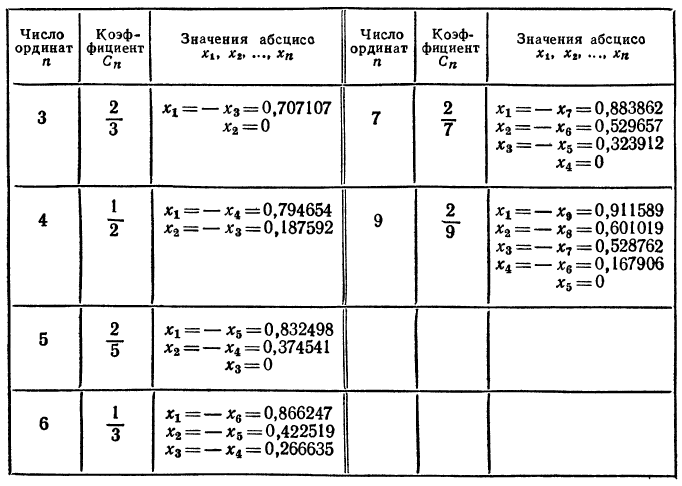
Таким образом, приближенное вычисление интеграла на от- резке [ — 1, 1] производится по следующей формуле Чебышева:

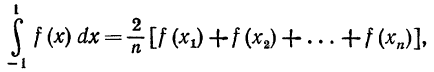
где n — какое-либо из чисел 3, 4, 5, 6, 7 или 9, a x_i,...,x_n - числа, приведенные в таблице. В качестве n нельзя брать число 8 или числа, превосходящие 9; в этом случае система уравнений (10) дает мнимые корни. Когда заданный интеграл имеет пределы интегрирования а и b, формула Чебышева принимает вид

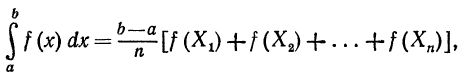
где 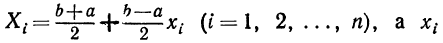имеют указанные в таблице значения.

Сравнивая этот результат с результатами вычисления по формулам прямоугольников, по формуле трапеций и формуле Симпсона (см. пример в предыдущем параграфе), мы замечаем, что результат, полученный нами по формуле Чебышева (с тремя промежуточными точками), лучше согласуется с истинным значением интеграла, чем результат, полученный по формуле трапеций (с девятью промежуточными точками).
Отметим, что теория приближенного вычисления интегралов получила дальнейшее развитие в работах академика А. Н. Крылова (1863-1945).