Глава I

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Глава II

Глава II

ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

$ 1. Постановка задачи. Нижняя и верхняя интегральные суммы

       Мощным средством исследования в математике, физике, механике и других дисциплинах является определенный интеграл—одно из основных понятий математического анализа. Вычисление площадей, ограниченных кривыми, длин дуг, объемов, работы, скорости, пути, моментов инерции и т. д. сводится к вычислению определенного интеграла.

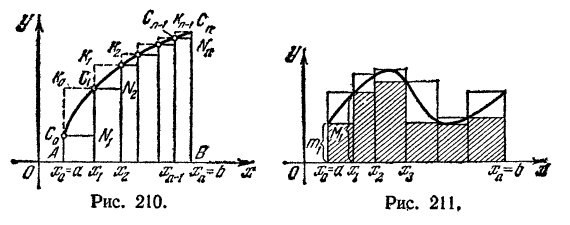
Пусть на отрезке [а, b] задана непрерывная функция y=f(x) (рис. 210 и 211). Обозначим через m и n ее наименьшее и наибольшее значения на этом отрезке. Разобьем отрезок [а, b] на n частей точками деления a=x₀, x₁,x₂,...,x_n-1,x_n=b причем x₀ < x ₁ < x₂ < ... < x_n, и положим 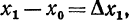х₂-х₁=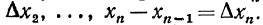Обозначим, далее, наименьшее и наибольшее значение функции f(x) на отрезке [x0,x1] через m1 и M1, на отрезке [x1,x2] через m2 и M2,...,на отрезке[x_n-1,x_nчерез m_n и M_n.Составим суммы

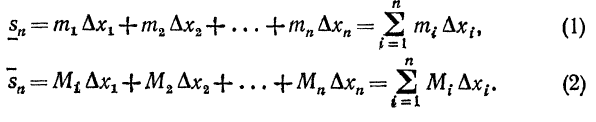
       Сумму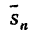 называют нижней интегральной суммой, а сумму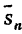верхней интегральной суммой.
       Если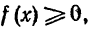то нижняя интегральная сумма числено равняется площади "вписанной ступенчатой фигуры" AC₀N₁C₁N₂...C_n-1N_nBA, ограниченной "вписаной" ломаной, верхняя интегральная сумма численно равняетсяплощади "описанной ступенчатой фигуры" 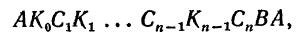ограниченной "описанной" ломаной.

       Отметим некоторые свойства верхних и нижних интегральных сумм.
       a) Так как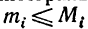 для любого i(i=1,2,3,...,n), то на основании формул (1) и (2) имеем

(Знак равенства будет только в случае, если f(x)=const)

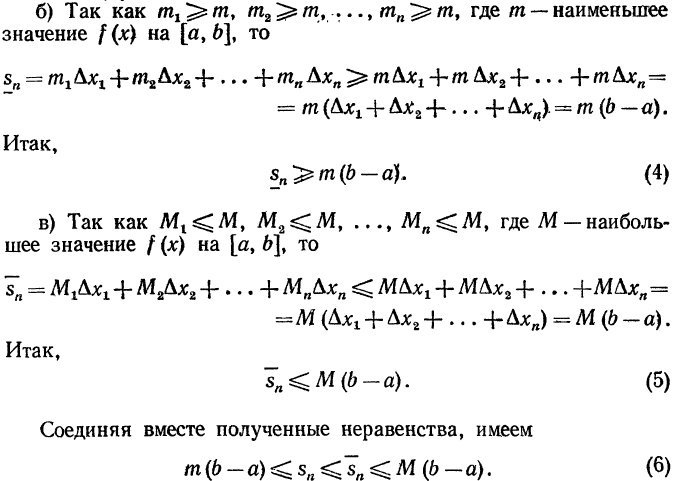
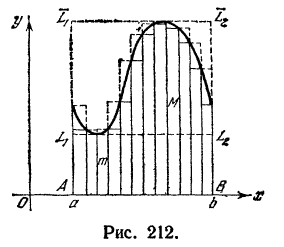
       Если 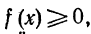то последнее неравенство имеет простой геометрический смысл (рис. 219), так как произведения m(b-a) и M(b-a) соответственно численно равны площадям "вписанного" прямоугольника LL₁L₂B и "описанного" прямоугольника