Электронный образовательный ресурс по теме
"Интегральные Исчисления"
"Интегральные Исчисления"
СОДЕРЖАНИЕ
Глава I
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
$ 1. Первообразная и неопределенный интеграл
$ 2. Таблица интегралов
$ 3. Некоторые свойства неопределенного интеграла
$ 4. Интегрирование методом замены переменной или способом подстановки
$ 5. Интегралы от некоторых функций, содержащих квадратный трехчлен
$ 6. Интегрирование по частям
$ 7. Рациональные дроби. Простейшие рациональные дроби и их интегрирование
$ 8. Разложение рациональной дроби на простейшие
$ 9. Интегрирование рациональных дробей
$ 10. Интегралы от иррациональных функций
$ 11. Интегрирование некоторых классов тригонометрических функций
$ 1. Постановка задачи. Нижняя и верхняя интегральные суммы
$ 2. Определенный интеграл. Теорема о существовании определенного
интеграла
$ 3. Основные свойства определенного интеграла
$ 4. Вычисление определенного интеграла. Формула Ньютона — Лейбница
$ 5. Замена переменной в определенном интеграле
$ 6. Интегрирование по частям
$ 7. Несобственные интегралы
$ 8. Приближенное вычисление определенных интегралов
$ 9. Формула Чебышева
$ 10. Интегралы, зависящие от параметра. Гамма-функция
$ 11. Интегрирование комплексной функции действительной переменной
$ 12. Геометрические и механические приложения определенного интеграла
$ 1. Определение двойного интеграла
$ 2. Замена переменных в двойном интеграле
$ 3. Приложения двойного интеграла.
$ 4. Тройной интеграл.
$ 1. Определение криволинейного интеграла второго рода
$ 2. Интеграл по замкнутому контуру
$ 3. Условия независимости интеграла от пути интегрирования.
$ 1. Поверхностные интегралы первого и второго рода.
$ 2. Формула Стокса.
$ 3. Формула Остроградского.
Глава I
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
$ 5. Интегрирование от некоторых функций, содержащих квадратный трехчлен
1. Рассмотрим интеграл
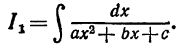
Преобразуем предварительно трехчлен, стоящий в знаменателе, представив его в виде суммы или разности квадратов:
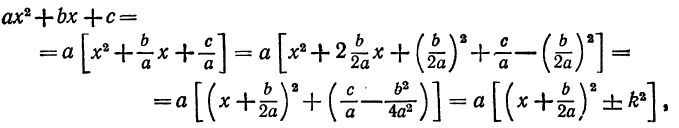
где обозначено 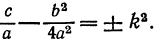 . Знак плюс или минус берется в зависимости от того, будет ли выражение, стоящее слева, положительным или отрицательным, т.е. будут ли корни трехчлена
. Знак плюс или минус берется в зависимости от того, будет ли выражение, стоящее слева, положительным или отрицательным, т.е. будут ли корни трехчлена 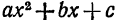 комплексными или действительными.
комплексными или действительными.
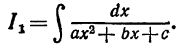
Таким образом, интеграл I1 принимает вид
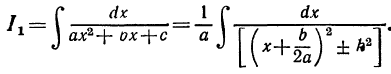
Сделаем в последнем интеграле замену переменной
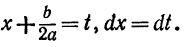
Тогда получим
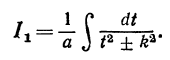
Это-табличные интегралы (см. формулы 11' и 12).
П р и м е р 1. Вычислить интеграл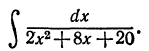
Р е ш е н и е.
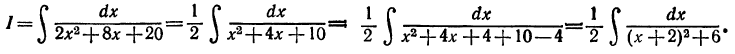
Делаем замену переменной x+2=t, dx=dt. Подставляя в интеграл, получаем табличный интеграл
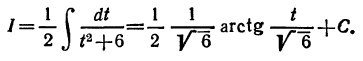
Подставляя вместо t его выражение через x, окончательно находим
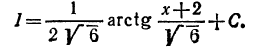
2. Рассмотрим интеграл более общего вида м
Произведем тождественное преобразование подынтегральной функции:
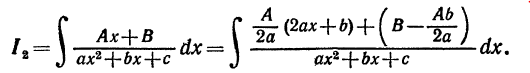
Последний интеграл представим в виде суммы двух интегралов. Вынося постоянные множители за знак интегралов, получим
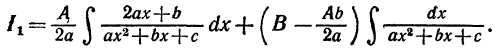
Второй интеграл есть интеграл I1, вычислять который мы умеем. В первом интеграле сделаем замену переменной
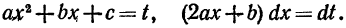
Следовательно,
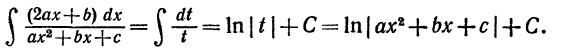
Таким образом, окончательно получаем
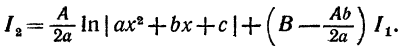
П р и м е р 2. Вычислить интеграл 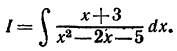
Применим указанный прием:
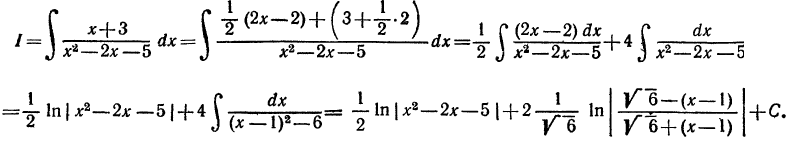
3. Рассмотрим интеграл
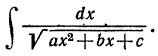
C помощью преобразований, рассмотренных в п.1, этот интеграл сводится, в зависимости от знака а, к табличным интегралам вида
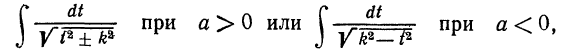
Которые уже рассмотрены в таблице интегралов (см. формулы 13' и 14).
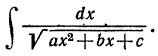
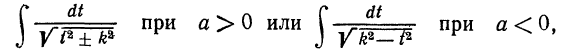
4. Интеграл вида
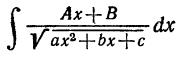
вычисляется с помощью следующих преобразования, аналогичных тем, которые были рассмотрены в п. 2:
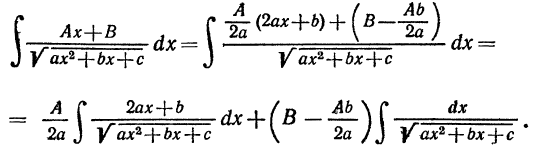
Применив к первому из полученных интегралов подстановку
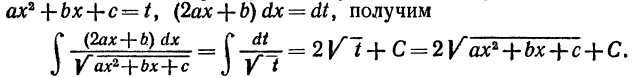
Второй же интеграл был рассмотрен нами в п.3 настоящего параграфа.