Глава I

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Глава II

Глава I

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

$ 1. Первообразная и неопределенный интеграл

В этой главе мы будем рассматривать следующую задачу: дана функция f (х); требуется найти такую функцию F (х), производная которой равна f(x) т. е. F'(x) = f(x).

Определение 1. Функция F(х) называется первообразной от функции f (х) на отрезке [a, b], если во всех точках этого отрезка выполняется равенство F'(x)=f(x).

Пример.

Найти первообразную от функции f(x)=x².

Из определения первообразной следует, что функция F(x)=x³/3 является первообразной, так как (х³/3)'=x²

Легко видеть, что если для данной функции f(x) существует первообразная, то эта первообразная не является единственной. Так, в предыдущем примере можно было взять в качестве первообразных следующие функции: 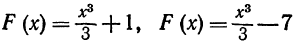или вообще 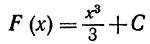(где С - произвольная постоянная), так как 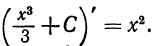. С другой стороны, можно доказать, что функциями вида 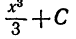исчерпываются все первообразные от функции x². Это вытекает из следующей теоремы.

Теорема. Если F₁(x) и F₂(x)— две первообразные от функции f(x) на отрезке [а, 6], то разность между ними равна постоянному числу.

Доказательство. В силу определения первообразной имеем

при любом значении х на отрезке [a,b].

Обозначим

Тогда на основании равенств (1) будет или при любом значении х на отрезке [a,b]. Но из равенства следует, что ф(х) есть постоянная.

Действительно, применим теорему Лагранжа (см. § 2 гл. IV) к функции ф (х), которая, очевидно, непрерывна и дифференцируема на отрезке [а, b]. Какова бы ни была точка х на отрезке [а, b], мы имеем в силу теоремы Лагранжа где

Так как или

Таким образом, функция ф(x) в любой точке х отрезка [а, b] со- храняет значение ф(а), а это и значит, что функция ф(x) является постоянной на отрезке [а, b]. Обозначая постоянную ф(а) через С, из равенств (2) и (3) получаем

Из доказанной теоремы следует, что если для данной функции f(x) найдена какая-нибудь одна первообразная F(x),тo любая другая первообразная для f(x) имеет вид F(x) + С, где С = const.

Определение 2. Если функция F (х) является первообраз- ной для f(x), то выражение F(x) + C называется неопределенным интегралом от функции f(х) и обозначается символом

Таким образом, по определению, еслиПри этом функцию f(x) называютподынтегральной функцией,f(x)dx-подынтегральным выражением, знак -знаком интеграла.

Таким образом, неопределенный интеграл представляет собой семейство функций y = F(x)+C.

С геометрической точки зрения неопределенный интеграл представляет совокупность (семейство) кривых, каждая из которых получается путем сдвига одной из кривых параллельно самой себе вверх или вниз, т. е. вдоль оси Оу.

Естественно возникает вопрос: для всякой ли функции f(x) существуют первообразные (а значит, и неопределенный интеграл)?

Оказывается, что не для всякой. Заметим, однако, без доказательства, что если функция f (x) непрерывна на отрезке [а, b], то для этой функции существует первообразная (а значит, и неопределенный интеграл).

Выяснению методов, с помощью которых находятся пераообразяые (и неопределенные интегралы) от некоторых классов элементарных функций, посвящена настоящая глава. Нахождение первообразной для данной функции f(x) называется интегрированием функции f(x).

Захметим следующее: если производная от элементарной функции всегда является элементарной функцией, то первообразная от элементарной функции может оказаться и не представимой с помощью конечного числа элементарных функций. К этому вопросу мы вернемся в конце данной главы.

Из определения 2 следует:

1. Производная от неопределенного интеграла равна подынтегральной функции, т. е. если , то и

Последнее равенство нужно понимать в том смысле, что производная от любой первообразной равна подынтегральной функции.

2. Дифференциал от неопределенного интеграла равен подынтегральному выражению:

Это получается на основании формулы (4).

3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная:

Справедливость последнего равенства легко проверить дифференцированием (дифференциалы от обеих частей равенства равны dF (x)).