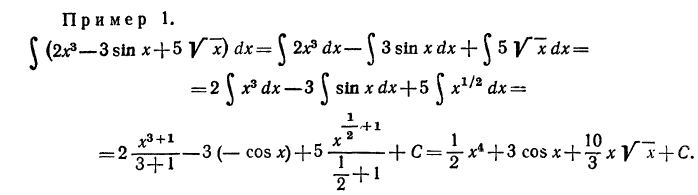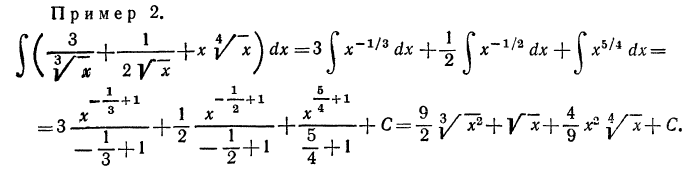Электронный образовательный ресурс по теме
"Интегральные Исчисления"
"Интегральные Исчисления"
СОДЕРЖАНИЕ
Глава I
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
$ 1. Первообразная и неопределенный интеграл
$ 2. Таблица интегралов
$ 3. Некоторые свойства неопределенного интеграла
$ 4. Интегрирование методом замены переменной или способом подстановки
$ 5. Интегралы от некоторых функций, содержащих квадратный трехчлен
$ 6. Интегрирование по частям
$ 7. Рациональные дроби. Простейшие рациональные дроби и их интегрирование
$ 8. Разложение рациональной дроби на простейшие
$ 9. Интегрирование рациональных дробей
$ 10. Интегралы от иррациональных функций
$ 11. Интегрирование некоторых классов тригонометрических функций
$ 1. Постановка задачи. Нижняя и верхняя интегральные суммы
$ 2. Определенный интеграл. Теорема о существовании определенного
интеграла
$ 3. Основные свойства определенного интеграла
$ 4. Вычисление определенного интеграла. Формула Ньютона — Лейбница
$ 5. Замена переменной в определенном интеграле
$ 6. Интегрирование по частям
$ 7. Несобственные интегралы
$ 8. Приближенное вычисление определенных интегралов
$ 9. Формула Чебышева
$ 10. Интегралы, зависящие от параметра. Гамма-функция
$ 11. Интегрирование комплексной функции действительной переменной
$ 12. Геометрические и механические приложения определенного интеграла
$ 1. Определение двойного интеграла
$ 2. Замена переменных в двойном интеграле
$ 3. Приложения двойного интеграла.
$ 4. Тройной интеграл.
$ 1. Определение криволинейного интеграла второго рода
$ 2. Интеграл по замкнутому контуру
$ 3. Условия независимости интеграла от пути интегрирования.
$ 1. Поверхностные интегралы первого и второго рода.
$ 2. Формула Стокса.
$ 3. Формула Остроградского.
Глава I
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
$ 3. Некоторые свойства неопределенного интеграла
Теорема 1. Неопределенный интеграл от алгебраической суммы
двух или нескольких функций равен алгебраической сумме их
интегралов:
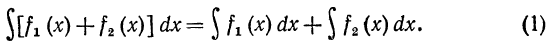
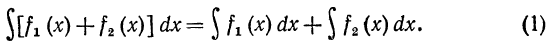
Для доказательства найдем производные от левой и правой
частей этого равенства. На основании равенства (4) § 1 находим
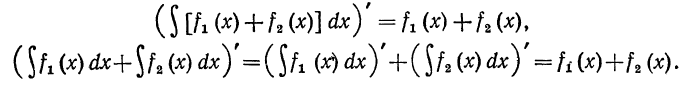
Таким образом, производные от левой и правой частей равенства (1) равны между собой, т. е. производная от любой первообразной, стоящая в левой части, равняется производной от любой функции, стоящей в правой части равенства. Следовательно, по теореме § 1 любая функция, стоящая в левой части равенства (1), отличается от любой функции, стоящей в правой части равенства (1), на постоянное слагаемое. В этом смысле и нужно понимать равен- ство (1).
Теорема 2. Постоянный множитель можно выносить за знак интеграла, т. е. если а = const, то
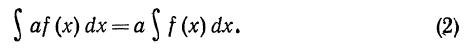
Для доказательства равенства (2) найдем производные от левой
и правой его частей: 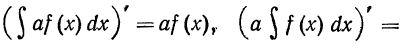
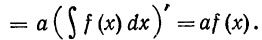
Производные от правой и левой частей равны, следовательно, как и в равенстве (1), разность двух любых функций, стоящих слева и справа, есть постоянная. В этом смысле и следует пони- мать равенство (2).
При вычислении неопределенных интегралов бывает полезно
иметь в виду следующие правила.
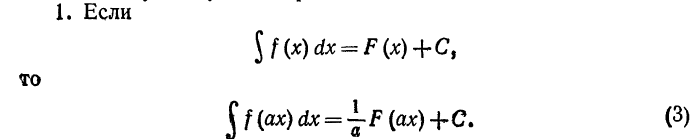
Действительно, дифференцируя левую и правую части равен-
ства (3), получим 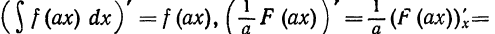
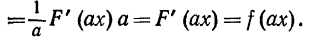
Производные от правой и левой частей равны, что и требовалось доказать.
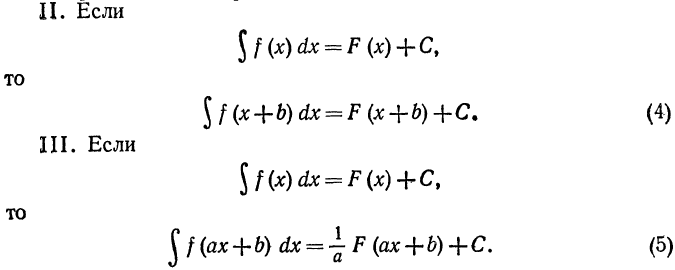
Равенства(4) и (5) доказываются дифференцированием правой и левой частей равенств.