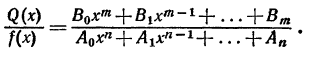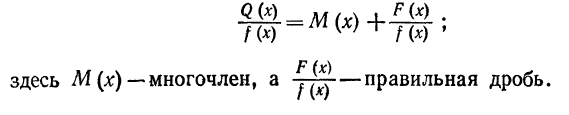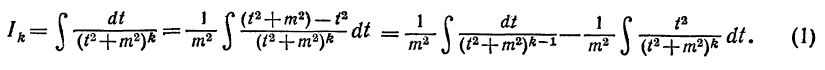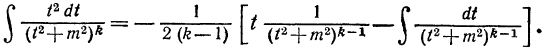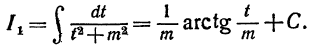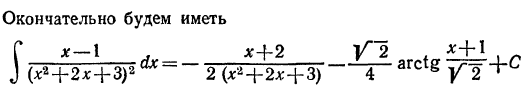Глава I

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Глава II

Глава I

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

$ 7. Рациональные дроби. Простейшие рациональные дроби и их интегрирование

Как мы увидим ниже, далеко не всякая элементарная функция имеет интеграл, выражающийся в элементарных функциях. Поэтому очень важно выделить такие классы функций, интегралы которых выражаются через элементарные функции. Простейшим из этих классов является класс рациональных функций.
       Всякую рациональную функцию можно представить в виде рациональной дроби, т. е. в виде отношения двух многочленов:
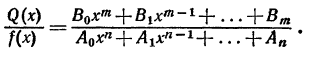
       Не ограничивая общности рассуждения, будем предполагать, что эти многочлены не имеют общих корней.
       Если степень числителя ниже степени знаменателя, то дробь называется правильной, в противном случае дробь называется неправильной.
       Если дробь неправильная, то, разделив числитель на знаменатель (по правилу деления многочленов), можно представить данную дробь в виде суммы многочлена и некоторой правильной дроби:

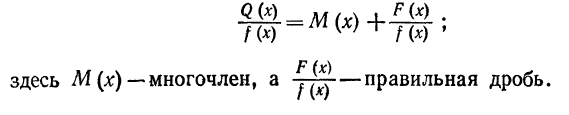
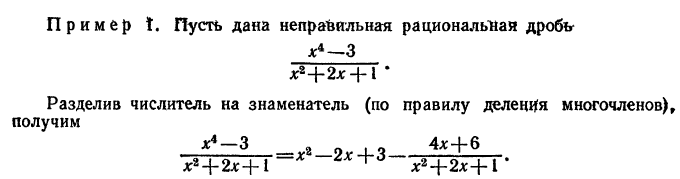
       Так как интегрирование многочленов не представляет затруднений, то основная трудность при интегрировании рациональных дробей заключается в интегрировании правильных рациональных дробей.

называются простейшими дробями I, II, III и IV типов.
       Далее будет доказано (см. §8), что всякую радцональную дробь можно представить в виде суммы простейших дробей. Поэтому мы рассмотрим сначала интегралы от простейших дробей.
Интегрирование простейших дробей типа I II и III не составляет большой трудности, поэтому мы проведем их интегрирование без каких-либо дополнительных пояснений:

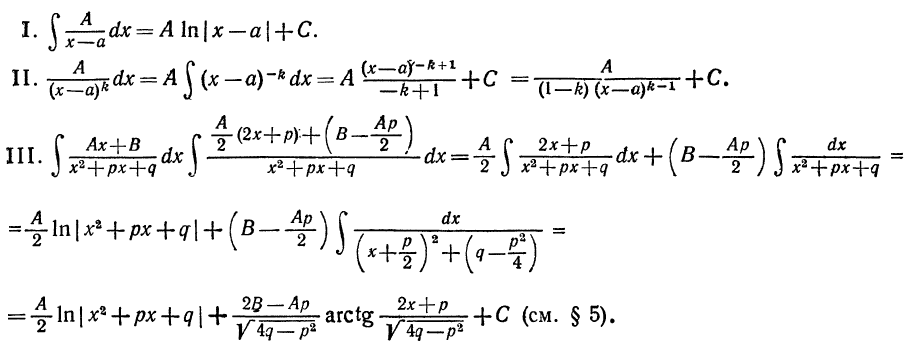
       Более сложных вычислений требует интегрирование простейших дробей IV типа. Пусть нам дан интеграл такого типа:

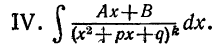
       Произведем преобразования:

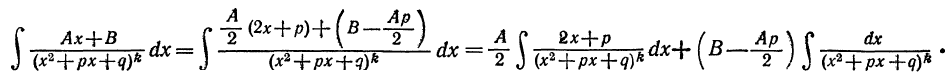
Первый интеграл берется подстановкой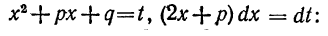

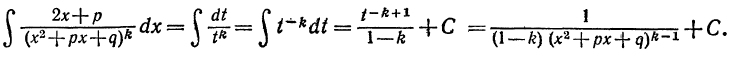
Второй интеграл-обозначим его через I_k-запишем в виде

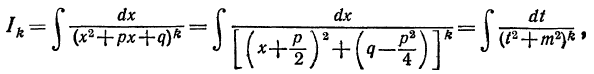
полагая

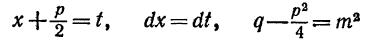
(по предположению корни знаменателя комплексные, а следовательно, 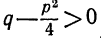). Далее поступаем следующим образом:

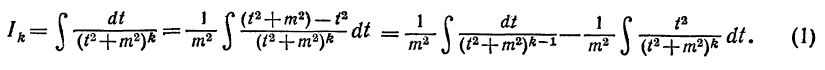
Преобразуем интеграл:

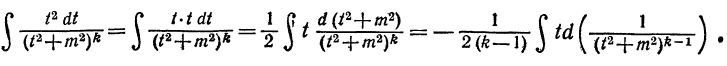
Интегрируя по частям, будем иметь

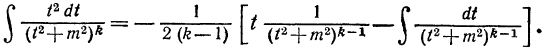
Подставляя это выражение в равенство (1), получим

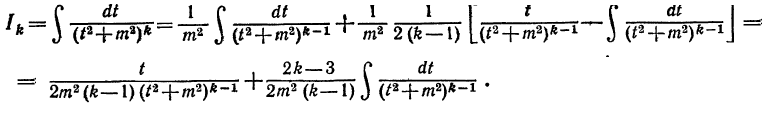
В правой части содержится интеграл того же типа, что I_k, но показатель степени знаменателя подынтегральной функции на единицу ниже (k —1); таким образом, мы выразили I_k через I_k-1.
Продолжая идти тем же путем, дойдем до известного интеграла:
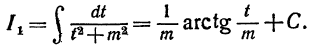
Подставляя затем всюду вместо t и m их значения, получим выражение интеграла IV черех х и заданные числа A,B,p,q