Глава I

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Глава II

Глава I

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

$ 6. Интегрирование по частям

Пусть u и v - две дифференцируемые функции от x. Тогда, как известно, дифференциал произведения uv вычисялется по следующей формуле: d(uv)=udv+vdu. Отсюда, интегрируя, получаем

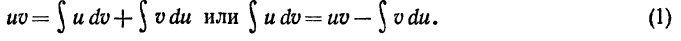
Последняя формула называется формулой интегрирования по частям. Эта формула чаще всего применяется к интегрированию выражений, которые можно так представить в виде произведения двух сомножителей u и dv чтобы отыскание функции v по ее дифференциалу dv и вычисление интеграла 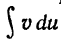составляли в совокупности задачу более простую, чем непосредственное вычисление интеграла 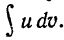Умение разбивать разумным образом данное подынтегральное выражение на множители u и v вырабатывается в процессе решения задач, и мы покажем на ряде примеров, как это делается.

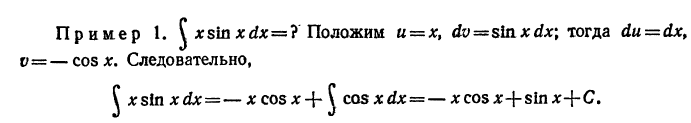
       З а м е ч а н и е. При определении функции v по дифференциалу dv мы можем брать любую произвольную постоянную, так как в конечный результат она не входит (что легко проверить, подставив в равенство (1) вместо v выражение v + C). Поэтому удобно считать эту постоянную равной нулю.
       Правило интегрирования по частям применяется во многих случаях. Так, например, интегралы вида
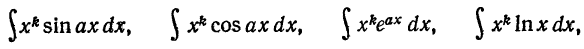
некоторые интегралы, содержащие обратные тригонометрические функции, вычисляются с помощью интегрирования по частям.