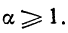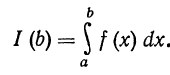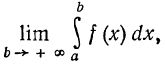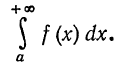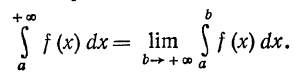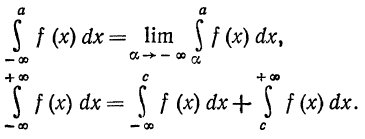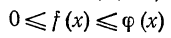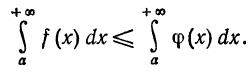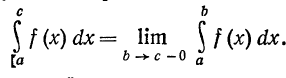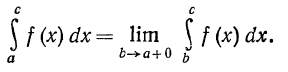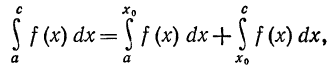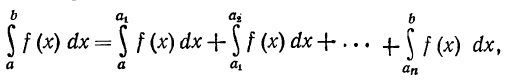Глава I

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Глава II

Глава II

ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

$ 7. Несобственные интегралы

       1. И н т е г р а л ы  с  б е с к о н е ч н ы м и  п р е д е л а м и. ПУсть функция f(x) определена и непрерывна при всех значениях х таких, что 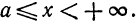Рассмотрим интеграл

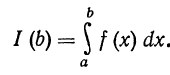
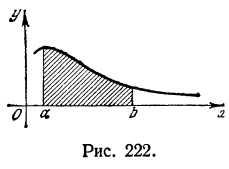
Этот интеграл имеет смысл при любом b > a. При изменении b интеграл изменяется, он является непрерывной функцией b (см. §4). Рассмотрим вопрос о поведении этого интеграла при 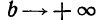(рис. 222)

       Определение. Если существует конечный предел

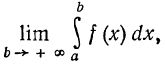
то этот предел называют несобственным интегралом от функции f(x) на интервале [а, +infinity) и обозначают так:

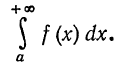
Следовательно, по определению имеем

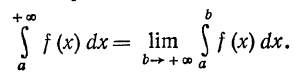
Говорят, что в этом случае несобственный интеграл 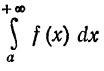существует или сходится. Есл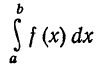и при 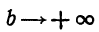не имеет конечного предела, то говорят, что 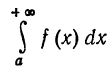не существует или расходится.
       Легко выяснить геометрический смысл несобственного интеграла в случае, когда f(x) > 0: если интеграл 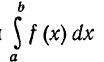выражает площадь области, ограниченной кривой y=f(x), осью абсцисс и ординатами x=a, x=b, то естественно считать, что несобственный интеграл 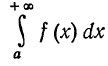выражает площадь неограниченной (бесконечной) области, заключенной между линиями y=f(x), x=a и осью абсцисс.

Аналогичным образом определяются несобственные интегралы и для других бесконечных интегралов:

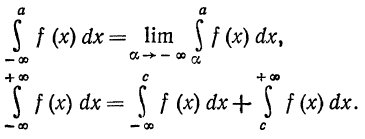
Последнее равенство следует понимать так: если каждый из несобственных интегралов, стоящих справа, существует, то существует (сходится) по определению и интеграл, стоящий слева.

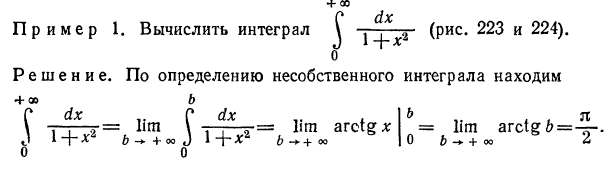
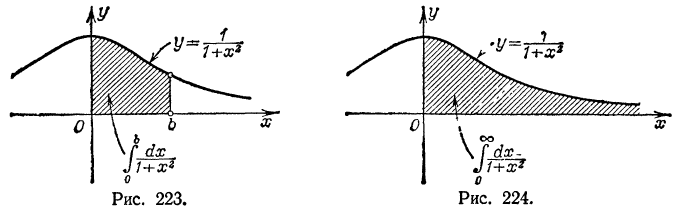
Рассмотренный интеграл выражает площадь бесконечной криволинейной трапеции, заштрихованной на рис. 224.

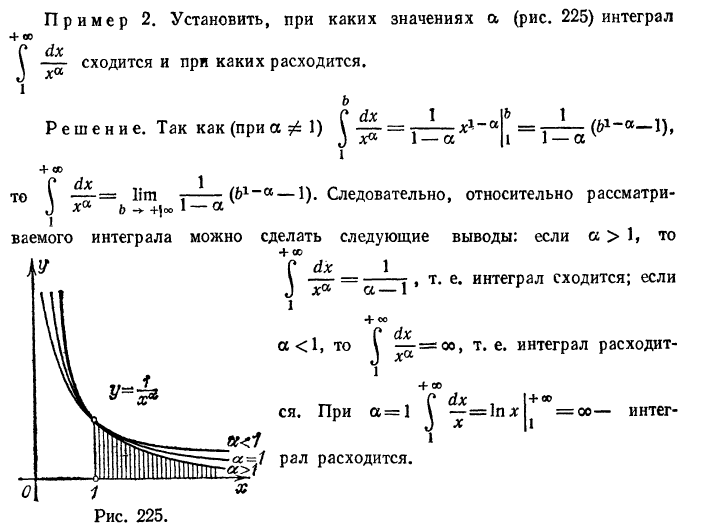
Во многих случаях бывает достаточно установить, сходится данный интеграл или расходится, и оценить его значение. Для этого могут быть полезными следующие теоремы, которые мы приведем без доказательств, а применение их докажем на примерах.
       Т е о р е м а 1. Если для всех х (х > a) выполняется неравенство

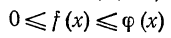
и если 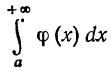сходится, то 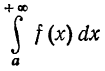так же сходится, при этом


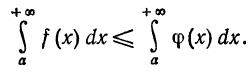
       Т е о р е м а 2. Если для всех х (х > a) выполняется неравенство 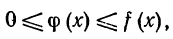причем 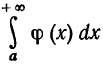расходится, то расходится и интеграл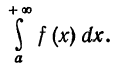

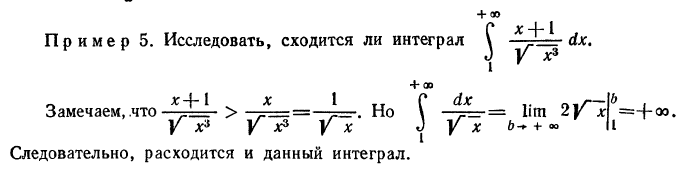
В последних двух теоремах рассматривались несобственные интегралы от неотрицательных функций. Для случая функции f(x), меняющей знак в бесконечном интервале, имеет место следующая теорема.
       Т е о р е м а 3. Если интеграл 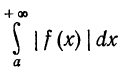сходится, то сходится и интеграл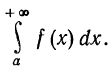
В этом случае последний интеграл называется абсолютно сходящимся.


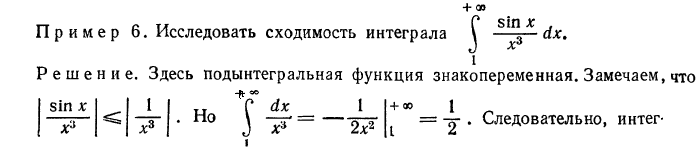
       2) И н т е г р а л  о т  р а з р ы в н о й  ф у н к ц и и.Пусть функция f(x) определена и непрерывна при 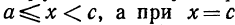функция либо не определена, либо терпит разрыв. В этом случае нельзя говорить об интеграле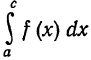как о пределе интегральных сумм, так как f(x) не непрерывна на отрезке [а, с], и поэ- тому этот предел может и не существовать.
Интеграл 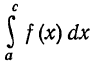от функции f (x), разрывной в точке с, определяется следующим образом:

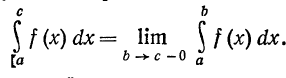
Если предел, стоящий справа, существует, то интеграл называют несобственным сходящимся интегралом, в противном случае интеграл называют расходящимся.
Если функция f (х) имеет разрыв в левом конце отрезка [а, с] (т. е. при х = а)у то по определению

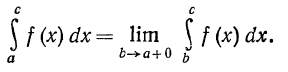
Если функция f(x) имеет разрыв в некоторой точке х = х₀ внутри отрезка [а, с], то полагают

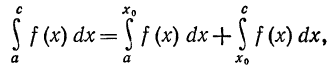
если оба несобственных интеграла, стоящих в правой части равен- ства, существуют.

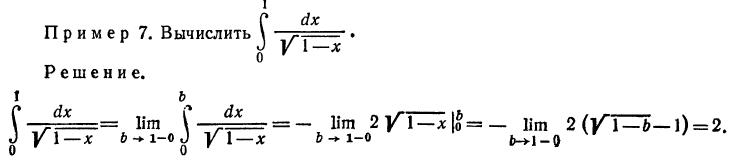
       Замечание. Если функция f(x), определенная на отрезке [a,b], имеет внутри этого отрезка конечное число точек а1,а2,...,а_n, то интеграл от функции f(x) на отрезке [a,b] определяется следующим образом:

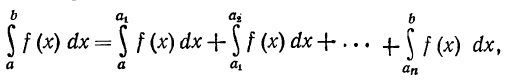
если каждый из несобственных интегралов в правой части равенства сходится. Если же хотя бы один из этих интегралов расходится, то и 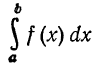называется расходящимся.

Для определения сходимости несобственных интегралов от разрывных функций и оценки их значений часто могут быть применены теоремы, аналогичные теоремам для оценки интегралов с бесконечными пределами.
       Теорема 1'. Если на отрезке [a,c] функции f(x) и ф(х) разрывны в точке с, причем во всех точках этого отрезка выполнены неравенства

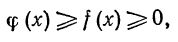
и 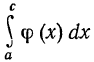сходится, то 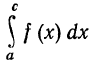также сходится.
       Теорема 2'. Если на отрезке [а, с] функции f (х) и ф(х) разрывны в точке с, причем во всех точках этого отрезка выполнены неравенства

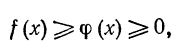
и 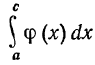расходится, то и 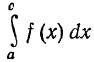расходится
       Теорема 3'. Если f(x) — функция, знакопеременная на отрезке [а, с], разрывная только в точке с, и несобственный интеграл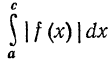 от абсолютной величины этой функции сходится, то сходится так же интеграл 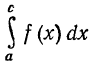от самой функции
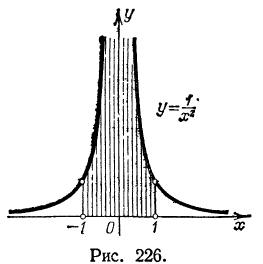
В качестве функций, с которыми удобно сравнивать функции, стоящие под знаком несобственного интеграла, часто берут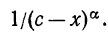Легко проверить, что 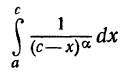сходится при a < 1, расходится при