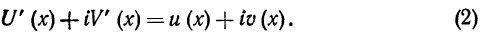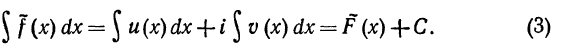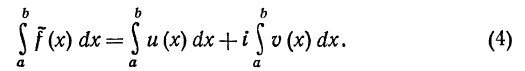Электронный образовательный ресурс по теме
"Интегральные Исчисления"
"Интегральные Исчисления"
СОДЕРЖАНИЕ
Глава I
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
$ 1. Первообразная и неопределенный интеграл
$ 2. Таблица интегралов
$ 3. Некоторые свойства неопределенного интеграла
$ 4. Интегрирование методом замены переменной или способом подстановки
$ 5. Интегралы от некоторых функций, содержащих квадратный трехчлен
$ 6. Интегрирование по частям
$ 7. Рациональные дроби. Простейшие рациональные дроби и их интегрирование
$ 8. Разложение рациональной дроби на простейшие
$ 9. Интегрирование рациональных дробей
$ 10. Интегралы от иррациональных функций
$ 11. Интегрирование некоторых классов тригонометрических функций
$ 1. Постановка задачи. Нижняя и верхняя интегральные суммы
$ 2. Определенный интеграл. Теорема о существовании определенного
интеграла
$ 3. Основные свойства определенного интеграла
$ 4. Вычисление определенного интеграла. Формула Ньютона — Лейбница
$ 5. Замена переменной в определенном интеграле
$ 6. Интегрирование по частям
$ 7. Несобственные интегралы
$ 8. Приближенное вычисление определенных интегралов
$ 9. Формула Чебышева
$ 10. Интегралы, зависящие от параметра. Гамма-функция
$ 11. Интегрирование комплексной функции действительной переменной
$ 12. Геометрические и механические приложения определенного интеграла
$ 1. Определение двойного интеграла
$ 2. Замена переменных в двойном интеграле
$ 3. Приложения двойного интеграла.
$ 4. Тройной интеграл.
$ 1. Определение криволинейного интеграла второго рода
$ 2. Интеграл по замкнутому контуру
$ 3. Условия независимости интеграла от пути интегрирования.
$ 1. Поверхностные интегралы первого и второго рода.
$ 2. Формула Стокса.
$ 3. Формула Остроградского.
Глава II
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
$ 11. Интегрирование комплексной функции
действительной переменной
Определение. Функция 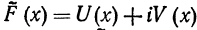 называется первообразной от комплексной функции
называется первообразной от комплексной функции 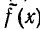 действительной переменной, если
действительной переменной, если

т.е. если
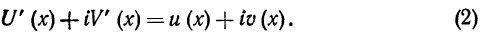
Из равенства (2) следует, что U' (х) = u(х), V (x) = v(x), т.е.
U(x) есть первообразная для u (х) и V (х) есть первообразная для
v(x).
Из определения и этого замечания следует: если 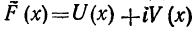 есть первообразная для функции
есть первообразная для функции 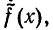 то любая первообразная для
то любая первообразная для 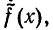 имеет вид
имеет вид 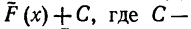 комплексная произвольная постоянная. ВЫражение
комплексная произвольная постоянная. ВЫражение 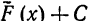 будем называть неопределенным интегралом от комплексной функции действительной переменной и писать
будем называть неопределенным интегралом от комплексной функции действительной переменной и писать
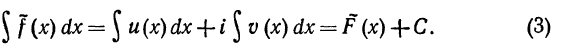
Определенный интеграл от комплексной функции f(x)=u(x)+iv(x) действительной переменной определяем так:
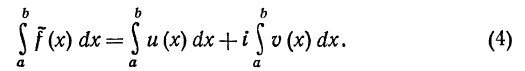
Это определение не противоречит, а вполне согласуется с оп-
ределением определенного интеграла как предела суммы.