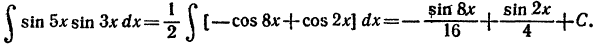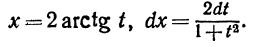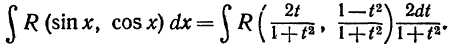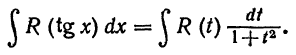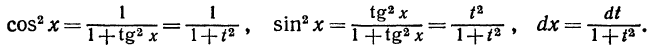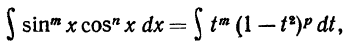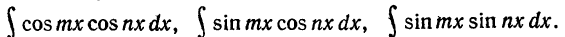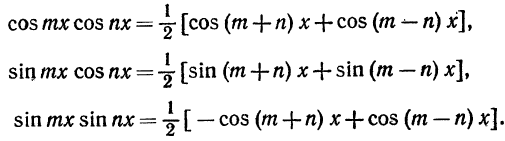Глава I

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Глава II

Глава I

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

$ 11. Интегрирование некоторых классов тригонометрических функций

       До сих пор мы систематически изучали интегралы только от алгебраических функций (рациональных и иррациональных). В настоящем параграфе мы рассмотрим интегралы от некоторых классов неалгебраических, в первую очередь тригонометрических функций. Рассмотрим интеграл вида

       Покажем, что этот интеграл с помощью подстановки

всегда сводится к интегралу от рациональной функции. Выразим sin x и cos x через 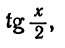а следовательно, и через t

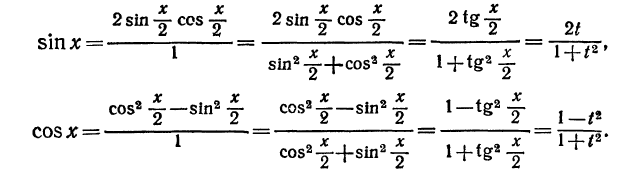
Далее

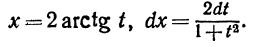
       ТАким образом, sinx, cosx и dxвыразились рационально через t. Так как рациональная функция от рациональных функций есть функция рациональная, то, подставляя полученные выражения в интеграл (1), получим интеграл от рациональной функции:


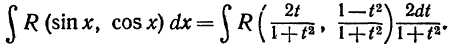
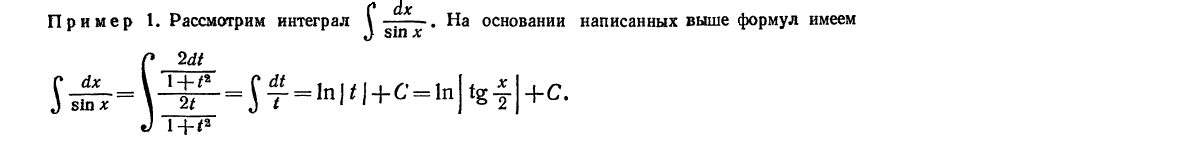
       Рассмотренная подстановка дает возможность проинтегрировать всякую функцию вида R(cosx, sin л:). Поэтому ее иногда называют «универсальной тригонометрической подстановкой». Однако на практике она часто приводит к слишком сложным рациональным функциям. Поэтому наряду с «универсальной» подстановкой бывает полезно знать также другие подстановки, которые в некоторых случаях быстрее приводят к цели.
1)Если интеграл имеет вид 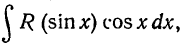то подстановка sinx=t, cosxdx=dt приводит этот интеграл к виду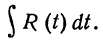
2)Если интеграл имеет вид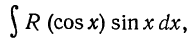то он приводится к интегралу от рациональной функции заменой cosx=t, sinxdx=-dt
3)Если подынтегральная функция зависит только от tgx, то замена tgx=t, x=arctgt, 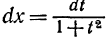приводит этот интеграл к интегралу от рациональной функции

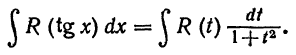
4)Если подынтегральная функция имеет вид R (sinx, cosx), но sinx и cosx входят только в четных степенях, то применяется та же подстановка

так как sin²x и cos²x выражаются рационально через tgx:

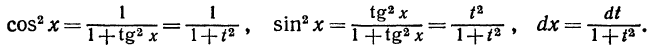
       После подстановки мы получим интеграл от рациональной функции.

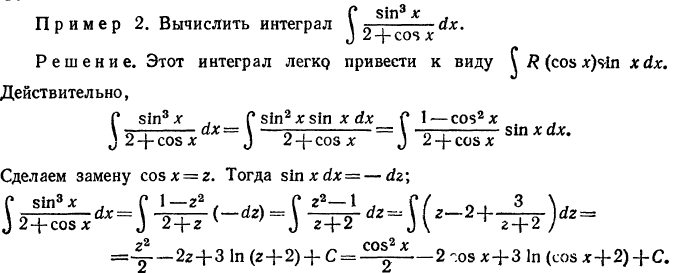
5)Рассмотрим теперь еще один интеграл вида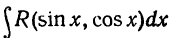-именно, интеграл, под знаком которого стоит произведение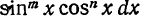(где m и n - целые числа). Здесь рассмотрим три случая.
       a)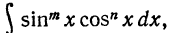где m и n таковы, что по крайней мере одно из них - н е ч е т н о е число. Допустим для определенности, что n нечетное. Положим n=2p+1 и преобразуем интеграл:

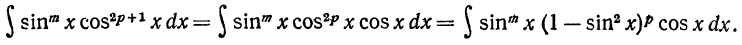
Сделаем замену переменной: sinx=t, cosxdx=dt. Подставляя новую переменную в данный интеграл, получим

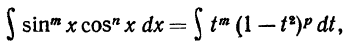
а это есть интеграл от рациональной функции от t

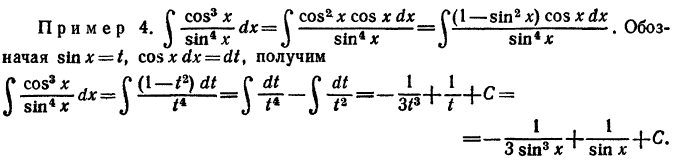
       б)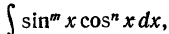где m и n - числа неотрицательные и четные. Положим m=2p, n=2q. Напишем формулы, известные из тригонометрии:

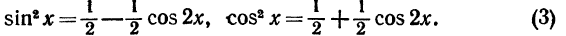
Подставляя в интеграл, получим

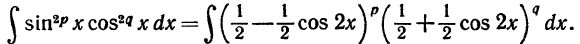
       Возводя в степень и раскрывая скобки, получим члены, содержащие cos2x в нечетных и четных степенях. Члены с нечетными степенями интегрируются, как указано в случае а). Четные показатели степеней снова понижаем по формулам (3). Продолжая так, дойдем до членов 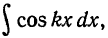которые легко интегрируются.

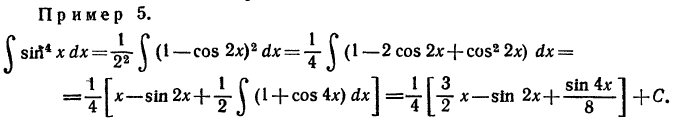
       в) Если оба показателя четные, причем хотя бы один из них отрицателен, то предыдущий прием не приводит к цели. Здесь следует сделать замену tgx=t (или ctgx=t)

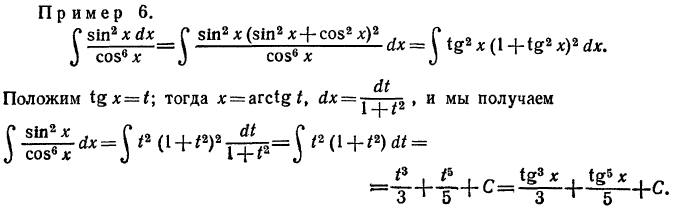
       6) Рассмотрим в заключение интегралы вида

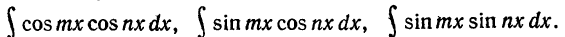
Они берутся при помощи следующих *) формул (m не равно n):

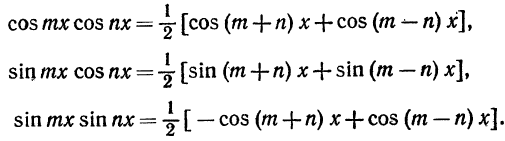
Подставляя и интегрируя, получим

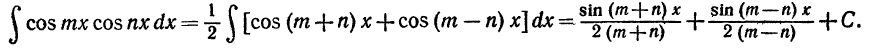
Аналогично вычисляются и два других интгерала.
П р и м е р 7.