
Электронный образовательный ресурс по теме
"Интегральные Исчисления"
"Интегральные Исчисления"
СОДЕРЖАНИЕ
Глава I
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
$ 1. Первообразная и неопределенный интеграл
$ 2. Таблица интегралов
$ 3. Некоторые свойства неопределенного интеграла
$ 4. Интегрирование методом замены переменной или способом подстановки
$ 5. Интегралы от некоторых функций, содержащих квадратный трехчлен
$ 6. Интегрирование по частям
$ 7. Рациональные дроби. Простейшие рациональные дроби и их интегрирование
$ 8. Разложение рациональной дроби на простейшие
$ 9. Интегрирование рациональных дробей
$ 10. Интегралы от иррациональных функций
$ 11. Интегрирование некоторых классов тригонометрических функций
$ 1. Постановка задачи. Нижняя и верхняя интегральные суммы
$ 2. Определенный интеграл. Теорема о существовании определенного
интеграла
$ 3. Основные свойства определенного интеграла
$ 4. Вычисление определенного интеграла. Формула Ньютона — Лейбница
$ 5. Замена переменной в определенном интеграле
$ 6. Интегрирование по частям
$ 7. Несобственные интегралы
$ 8. Приближенное вычисление определенных интегралов
$ 9. Формула Чебышева
$ 10. Интегралы, зависящие от параметра. Гамма-функция
$ 11. Интегрирование комплексной функции действительной переменной
$ 12. Геометрические и механические приложения определенного интеграла
$ 1. Определение двойного интеграла
$ 2. Замена переменных в двойном интеграле
$ 3. Приложения двойного интеграла.
$ 4. Тройной интеграл.
$ 1. Определение криволинейного интеграла второго рода
$ 2. Интеграл по замкнутому контуру
$ 3. Условия независимости интеграла от пути интегрирования.
$ 1. Поверхностные интегралы первого и второго рода.
$ 2. Формула Стокса.
$ 3. Формула Остроградского.
Глава II
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
$ 8. Приближенное вычисление определенных интегралов
В конце главы X указывалось, что не для всякой непрерыв-
ной функции ее первообразная выражается через элементарные
функции. В этих случаях вычисление определенных интегралов по
формуле Ньютона — Лейбница затруднительно, и применяются различные методы приближенного вычисления определенных
интегралов. Сейчас мы изложим несколько способов приближенного интегрирования, исходя из понятия определенного интеграла как предела суммы.
I. Формула прямоугольников. Пусть на отрезке [а, b] задана непрерывная функция y = f(x). Требуется вычислить определенный интеграл 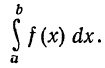
Разделим отрезок [а, b] точками a=x0,x1,x2,...,xn=b на n равных частей длины 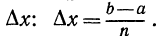
Обозначим далее через y0,y1,y2,...,yn-1,yn значения функции f(x) в точках x0,x1,x2,...,xn, т.е. y0=f(x0),y1=f(x1),...,yn=f(xn)
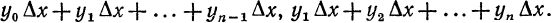
Каждая из этих сумм является интегральной суммой для f (х)
на отрезке [а, b] и поэтому приближенно выражает интеграл:
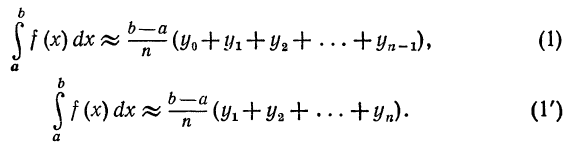
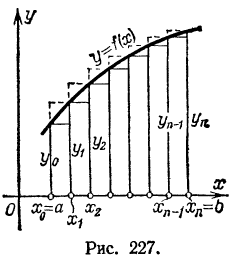
Это и будут формулы прямоугольников. Из рис. 227 ясно, что
если f (х) — положительная и возрастающая функция, то формула
(1) выражает площадь ступенчатой фигуры, составленной из
«входящих» прямоугольников, а формула (1') — площадь ступенчатой фигуры, состоящей из «выходящих» прямоугольников.
Ошибка, совершаемая при вычислении интеграла по формуле
прямоугольников, будет тем меньше, чем больше число n (т. е. чем
меньше шаг деления 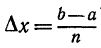 ).
).
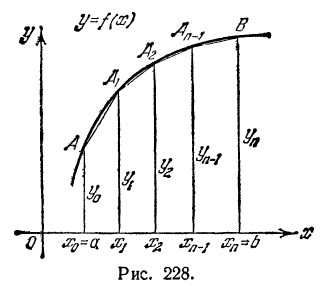
II. Формула трапеций. Естественно ожидать, что мы получим более точное значение определенного интеграла, если данную кривую y = f(x) заменим не ступенчатой линией, как это было в формуле прямоугольников, а вписанной ломаной (рис. 228), Тогда площадь криволинейной трапеции аАВb заменится суммой площадей прямолинейных трапеций, ограниченных сверху хордами 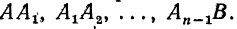 Так как площадь первой из этих трапеций равна
Так как площадь первой из этих трапеций равна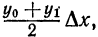 площадь второй равна
площадь второй равна 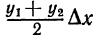 и т.д., то
и т.д., то
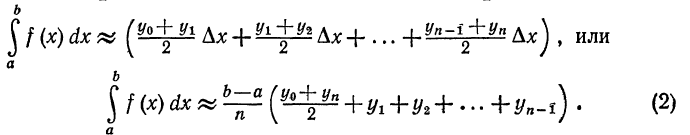
Это и есть формула трапеций. Отметим, что число, стоящее в
правой части формулы B), есть среднее арифметическое чисел,
стоящих в правых частях формул (1) и (1').
Число n выбирается произвольно. Чем больше будет это число
и чем меньше, следовательно, будет шаг 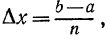 тем с большей точностью сумма, написанная в правой части приближенного равенства (2), будет давать значение интеграла.
тем с большей точностью сумма, написанная в правой части приближенного равенства (2), будет давать значение интеграла.
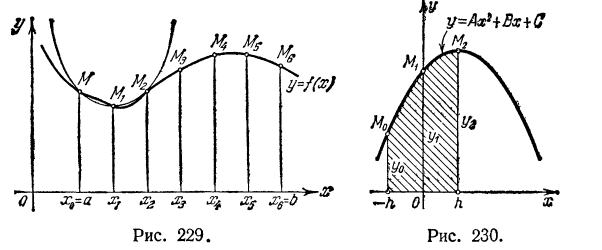
III. Формула парабол (формула Симпсона). Разделим отрезок [а, b] на четное число равных частей n = 2m. Площадь криволинейной трапеции,
соответствующей первым двум отрезкам [x0,x1] и [x1, x2] и ограниченной заданной кривой y=f(x), заменим площадью криволинейной трапеции, которая ограничена параболой второй степени, проходящей через три точки 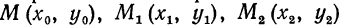 и имеющей ось, параллельную оси Оy (рис. 229). Такую криволинейную трапецию будем называть параболической трапецией.
и имеющей ось, параллельную оси Оy (рис. 229). Такую криволинейную трапецию будем называть параболической трапецией.
Уравнение параболы с осью, параллельной оси Оу, имеет вид
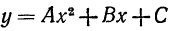
Коэффициенты A, В и С однозначно определяются из условия,
что парабола проходит через три заданные точки. Аналогичные
параболы строим и для других пар отрезков. Сумма площадей
параболических трапеций и даст приближенное значение интеграла.
Вычислим сначала площадь одной параболической трапеции.
Лемма. Если криволинейная трапеция ограничена параболой
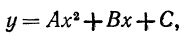
осью Ох и двумя ординатами, расстояние между которыми равно
2h, то ее площадь равна
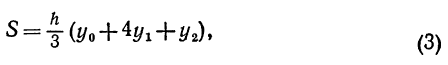
где у0 и у2 — крайние ординаты, а у1 — ордината кривой в середине
отрезка.
Доказательство. Расположим вспомогательную систему координат так, как показано на рис. 230.
Коэффициенты в уравнении параболы 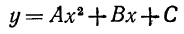 определяются из следующих уравнений:
определяются из следующих уравнений:
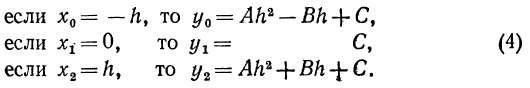
Считая коэффициенты А, В, С известными, определим площадь
параболической трапеции с помощью определенного интеграла:
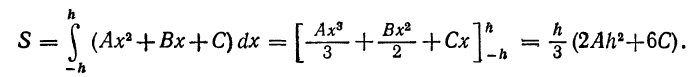
Но из равенств (4) следует, что 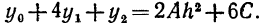 Следовательно,
Следовательно, 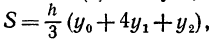 что и требовалось доказать.
что и требовалось доказать.
Вернемся снова к основной нашей задаче (см. рис. 229).
Пользуясь формулой (3), мы можем написать следующие приближенные равенства 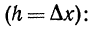
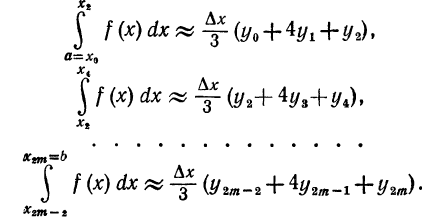
Складывая левые и правые части, получим слева искомый
интеграл, справа его приближенное значение:
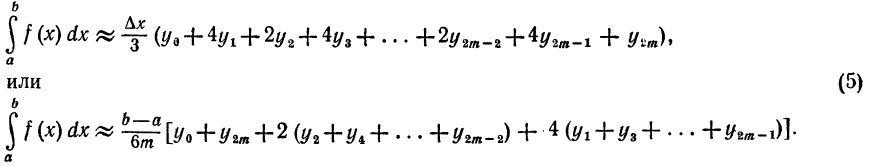
Это и есть формула Симпсона. Здесь число точек деления 2m
произвольно, но чем больше это число, тем точнее сумма в пра-
вой части равенства (5) дает значение интеграла *).
Пример. Вычислить приближенно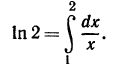
Решение. Разделим отрезок [1,2] на 10 равных частей (рис. 231). Полагая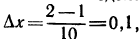 составим таблицу значений подынтегральной функции:
составим таблицу значений подынтегральной функции:

I. По первой формуле прямоугольников (1) получим
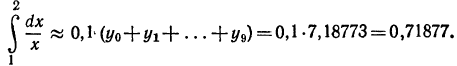
По второй формуле прямоугольников (1') получим
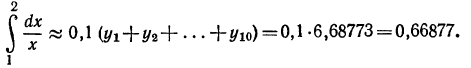
Непосредственно из рис. 231 следует, что в данном случае первая фор-
мула дает значение интеграла с избытком, вторая — с недостатком.
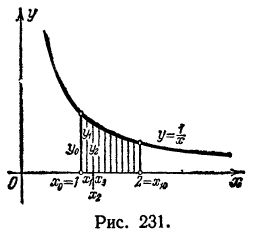
II. По формуле трапеций (2) получим
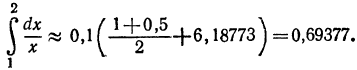
III. По формуле Симпсонв (5) имеем
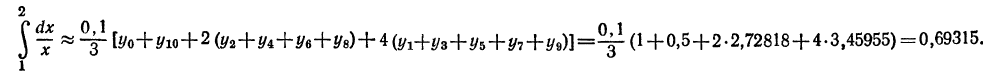
В действительности 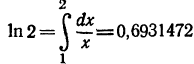 (с точностью до седьмого знака)
(с точностью до седьмого знака)
Таким образом, при разбиении отрезка [0, 1] на 10 частей по формуле
Симпсона мы получили пять верных знаков; по формуле трапеций—лишь три
верных знака; по формуле прямоугольников мы можем ручаться только за
первый знак.

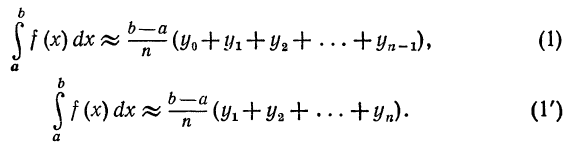
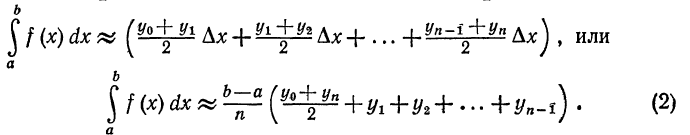

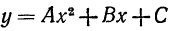
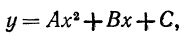
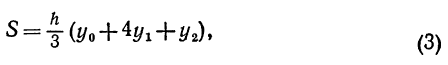

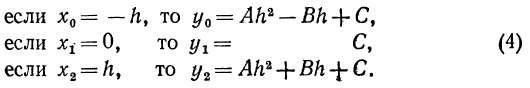
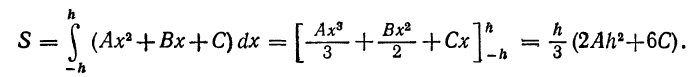
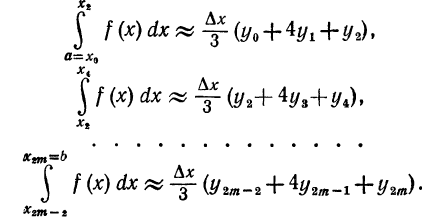
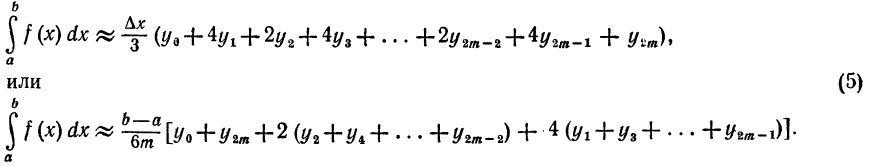
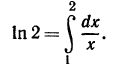
Решение. Разделим отрезок [1,2] на 10 равных частей (рис. 231). Полагая
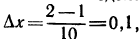 составим таблицу значений подынтегральной функции:
составим таблицу значений подынтегральной функции:
I. По первой формуле прямоугольников (1) получим
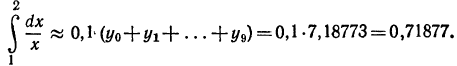
По второй формуле прямоугольников (1') получим
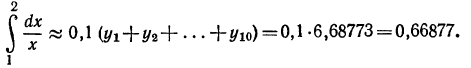
Непосредственно из рис. 231 следует, что в данном случае первая фор- мула дает значение интеграла с избытком, вторая — с недостатком.

II. По формуле трапеций (2) получим
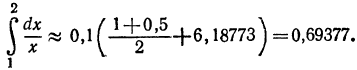
III. По формуле Симпсонв (5) имеем
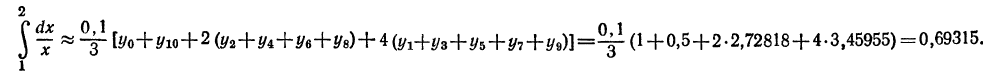
В действительности
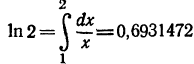 (с точностью до седьмого знака)
(с точностью до седьмого знака)Таким образом, при разбиении отрезка [0, 1] на 10 частей по формуле Симпсона мы получили пять верных знаков; по формуле трапеций—лишь три верных знака; по формуле прямоугольников мы можем ручаться только за первый знак.