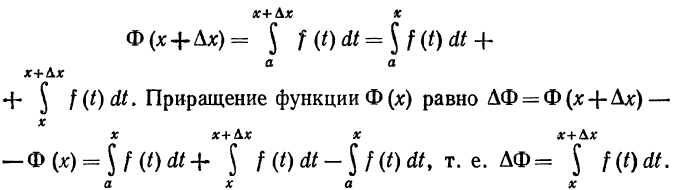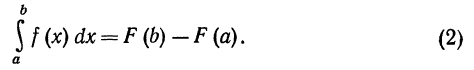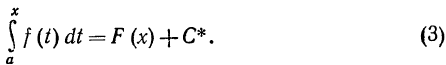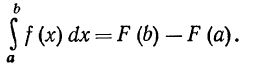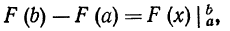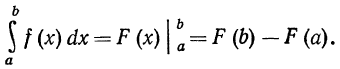Глава I

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Глава II

Глава II

ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

$ 4. Вычисление определенного интеграла. Формула Ньютона — Лейбница

       Пусть в определенном интеграле 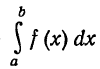нижний предел а закреплен, а верхний предел b меняется. Тогда будет меняться и значение интеграла, т.е. интеграл есть функция верхнего предела.
       Для того чтобы иметь привычные обозначения, верхний предел обозначим через х, а чтобы не смешивать его с переменной интегрирования, последнюю обозначим через t. (От обозначения переменной интегрирования значение интеграла не зависит.) Получим интеграл 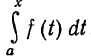. При постоянном а этот интеграл будет представлять собой функцию верхнего предела х. Эту функцию мы обозначим через Ф (х):

       Если f(t) - неотрицательная функция, то величина Ф(х) численно равна площади криволинейной трапеции aAXx(рис. 220).
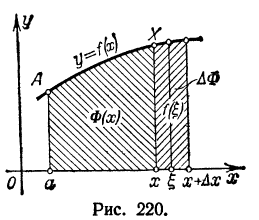
Очевидно, что эта площадь изменяется в зависимости от изменения х.
Найдем производную от Ф(х) по х, т.е. найдем производную определенного интеграла (1) по верхнему пределу.
       Т е о р е м а 1. Если f(x) - непрерывная функция и 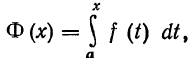то имеет место равенство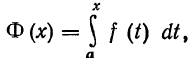
       Иными словами, производная от определенного интеграла по верхнему пределу равна подынтегральной функции, в которую вместо переменной интегрирования подставлено значение верхнего предела (при условии, что подынтегральная функция непрерывна).
       Д о к а з а т е л ь с т в о. Дадим аргументу х положительное или отрицательное приращение 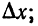тогда (учитывая свойство 6 определенного интеграла) получим

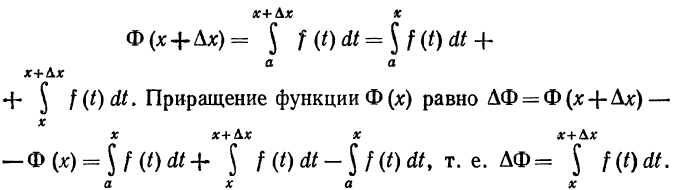
К последнему интегралу применим теорему о среднем значении (свойство 5 определенного интеграла)

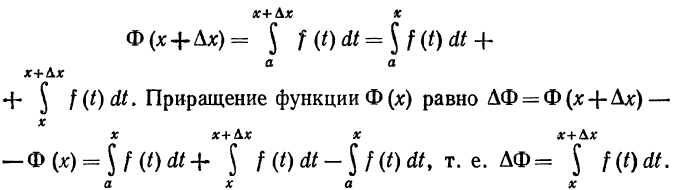
где 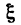заключено между х и х+/\х.
Найдем отношение приращения функции к приращению аргумента: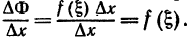

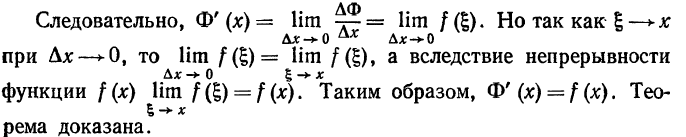
       Данная теормера просто иллюстрируется геометрически (рис. 220): приращение 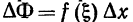равняется площади криволинейной трапеции с основанием /\х, а производная Ф'(x)=f(x) равна длине отрезка хХ.
       Т е о р е м а 2. Если F (х) есть какая-либо первообразная от непрерывной функции f(x), то справедлива формула

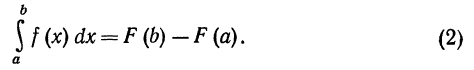
Эта формула называется формулой Ньютона-Лейбница*).
       Д о к а з а т е л ь с т в о. Пусть F (х) есть некоторая первообразная от функции f (х). По теореме 1 функция 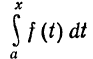есть также первообразная от f(x). Но две любые первообразные от данной функции отличаются на постоянное слагаемое С*. Следовательно, можно написать
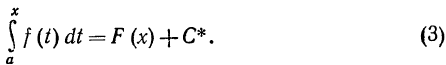
Это равенство при соответствующем выборе С* справедливо при всех значениях х, т. е. является тождеством. Для определения постоянного С* положим в этом тождестве х — а; тогда

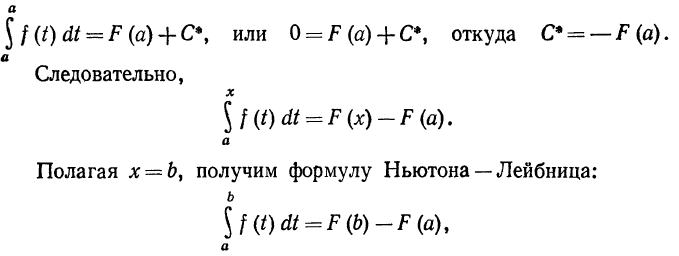
или, заменив обозначение переменной интегрирования на х:

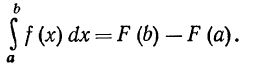
Отметим, что разность F (b) — F (а) не зависит от выбора первообразной F, так как все первообразные отличаются на постоянную величину, которая при вычитании все равно уничтожается. Если ввести обозначение *)

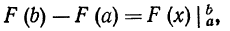
то формулу (2) можно переписать так:
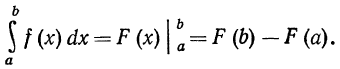
       Формула Ньютона — Лейбница дает практически удобный метод вычисления определенных интегралов в том случае, когда известна первообразная подынтегральной функции. Только с открытием этой формулы определенный интеграл смог получить то значение в математике, какое он имеет в настоящее время. Хотя с процессом, аналогичным вычислению определенного интеграла как предела интегральной суммы, были знакомы еще в древности (Архимед), однако приложения этого метода ограничивались теми простейшими случаями, когда предел интегральной суммы мог быть вычислен непосредственно. Формула Ньютона — Лейбница значительно расширила область применения определенного интеграла, так как математика получила общий метод для решения различных задач частного вида и поэтому смогла значительно расширить круг приложений определенного интеграла к технике, механике, астрономии и т. д.