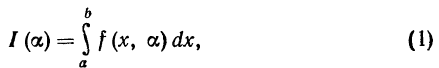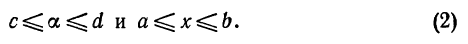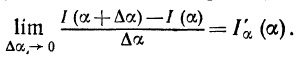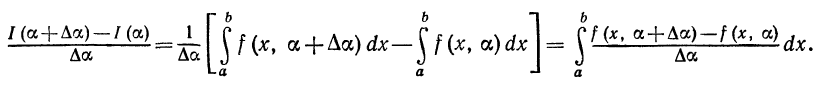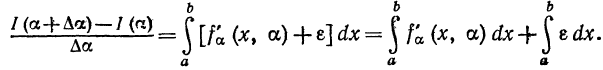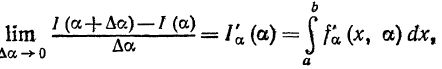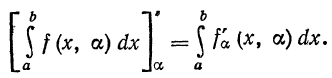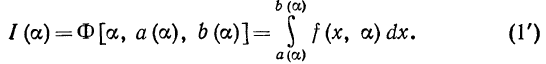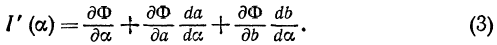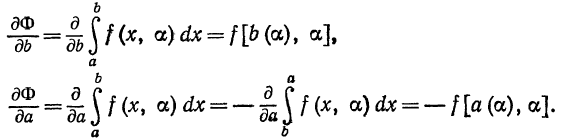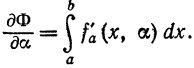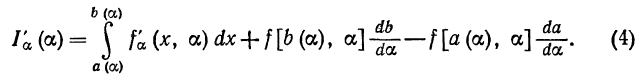Электронный образовательный ресурс по теме
"Интегральные Исчисления"
"Интегральные Исчисления"
СОДЕРЖАНИЕ
Глава I
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
$ 1. Первообразная и неопределенный интеграл
$ 2. Таблица интегралов
$ 3. Некоторые свойства неопределенного интеграла
$ 4. Интегрирование методом замены переменной или способом подстановки
$ 5. Интегралы от некоторых функций, содержащих квадратный трехчлен
$ 6. Интегрирование по частям
$ 7. Рациональные дроби. Простейшие рациональные дроби и их интегрирование
$ 8. Разложение рациональной дроби на простейшие
$ 9. Интегрирование рациональных дробей
$ 10. Интегралы от иррациональных функций
$ 11. Интегрирование некоторых классов тригонометрических функций
$ 1. Постановка задачи. Нижняя и верхняя интегральные суммы
$ 2. Определенный интеграл. Теорема о существовании определенного
интеграла
$ 3. Основные свойства определенного интеграла
$ 4. Вычисление определенного интеграла. Формула Ньютона — Лейбница
$ 5. Замена переменной в определенном интеграле
$ 6. Интегрирование по частям
$ 7. Несобственные интегралы
$ 8. Приближенное вычисление определенных интегралов
$ 9. Формула Чебышева
$ 10. Интегралы, зависящие от параметра. Гамма-функция
$ 11. Интегрирование комплексной функции действительной переменной
$ 12. Геометрические и механические приложения определенного интеграла
$ 1. Определение двойного интеграла
$ 2. Замена переменных в двойном интеграле
$ 3. Приложения двойного интеграла.
$ 4. Тройной интеграл.
$ 1. Определение криволинейного интеграла второго рода
$ 2. Интеграл по замкнутому контуру
$ 3. Условия независимости интеграла от пути интегрирования.
$ 1. Поверхностные интегралы первого и второго рода.
$ 2. Формула Стокса.
$ 3. Формула Остроградского.
Глава II
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
$ 10. Интегралы, зависящие от параметра. Гамма-функция
Дифференцирование интегралов, зависящих от параметра. Пусть дан интеграл
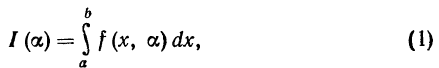
в котором подынтегральная функция зависит от некоторого параметра а. Если параметр а будет меняться, то будет меняться и
значение определенного интеграла. Таким образом, определенный
интеграл есть функция от а; поэтому мы его можем обозначить
через I (а).
1. Предположим, что 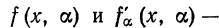 непрерывные функции при
непрерывные функции при
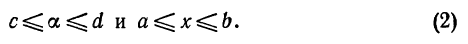
Найдем производную интеграла по параметру a:
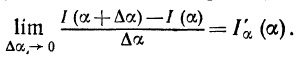
Для нахождения этой производной заметим, что
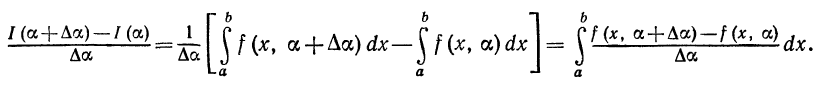
Применяя теорему Лагранжа к подынтегральной функции, будем
иметь 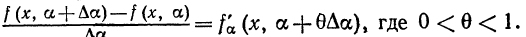 Так как
Так как 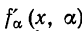 непрерывна а замкнутой области (2), то
непрерывна а замкнутой области (2), то 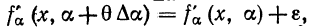 где величина
где величина 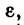 зависящая от
зависящая от 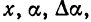 стремится у нулю при
стремится у нулю при 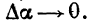 Таким образом,
Таким образом,
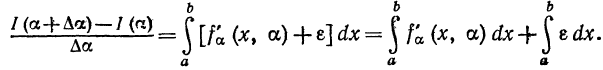
Переходя к пределу при 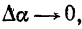 получаем *)
получаем *)
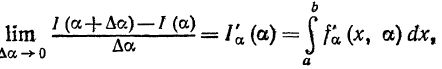
или
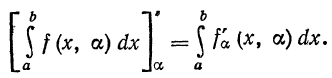
Последняя формула называется формулой Лейбница.
2. Предположим теперь, что в интеграле (1) пределы интегрирования a и b являются функциями от а:
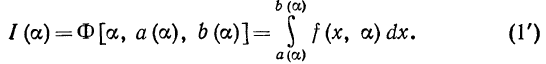
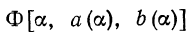 есть сложная функция от a, причем а и b являются промежуточными аргументами. Для того чтобы найти
производную от I (а), применим правило дифференцирования сложной функции от нескольких переменных
есть сложная функция от a, причем а и b являются промежуточными аргументами. Для того чтобы найти
производную от I (а), применим правило дифференцирования сложной функции от нескольких переменных
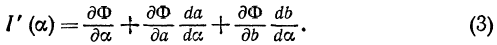
На основании теоремы о дифференцировании определенного
интеграла по переменному верхнему пределу (см. § 4) получаем
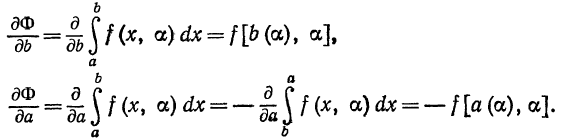
Наконец, для вычисления 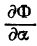 применяем формулу Лейбница:
применяем формулу Лейбница:
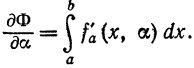
Подставляя в формулу (3) полученные выражения производных, будем иметь:
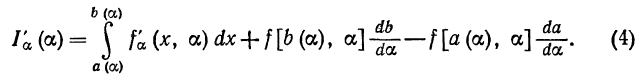
С помощью формулы Лейбница можно вычислить некоторые определенные интегралы.