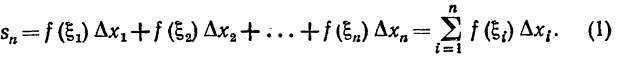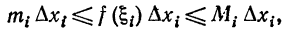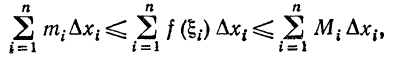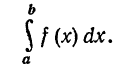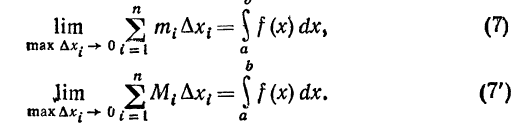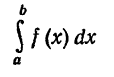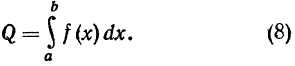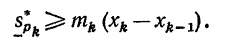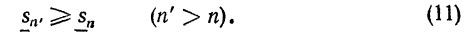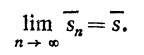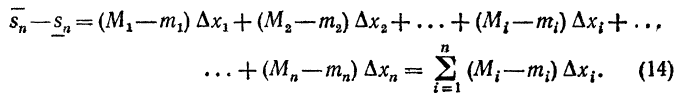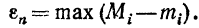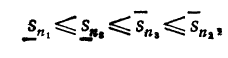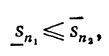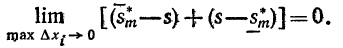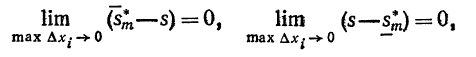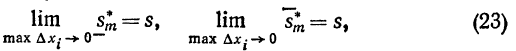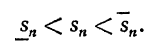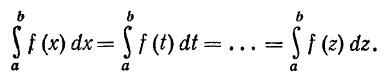Глава I

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Глава II

Глава II

ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

$ 2. Определенный интеграл. Теорема о существовании определенного интеграла

       Продолжим рассмотрение вопроса предыдущего параграфа. В каждом из отрезков [x0,x1],[x1,x2],...,[x_n-1,x_n] возьмем по точке, которые обозначим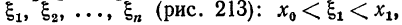

В каждой из этих точек вычислим значение функцииСоставим сумму

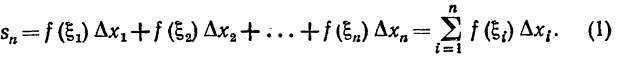
Эта сумма называется интегральной суммой для функции f(x) на отрезке [a,b]. Так как при произвольном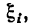 принадлежащем отрезку [x_i-1,x_i], будет

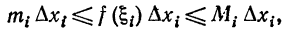
следовательно,

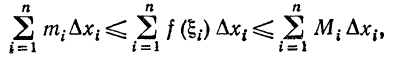
или
Геометрический смысл последнего неравенства при 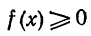состоит в том, что фигура, площадь которой равна s_n, ограничена ломаной, заключенной между «вписанной» ломаной и «описанной» ломаной.
       Сумма s_n зависит от способа разделения отрезка [a,b] на отрезки[x_i-1,x_i] и от выбора точек 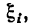внутри получающихся отрезков.
       Обозначим теперь через max[x_i-1,x_i] наибольшую из длин отрезков [x0,x1],[x1,x2],...,[x_i-1,x_i]. Рассмотрим различные разбиения отрезка [a,b] на отрезки [x_i-1,x_i] такие, что 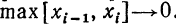Очевидно, что при этом число отрезков n в разбиении стремится к бесконечности. Для каждого разбиения, выбрав соответствующие значения 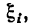можно составить интегральную сумму

       Рассмотрим некоторую последовательность разбиений, при котрых 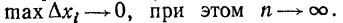При каждом разбиении выбираем значения 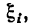. Предположим, что эта последовательность интегральных сумм *)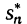стремится к некоторому пределу

       Теперь мы можем сформулировать следующее
       О п р е д е л е н и е 1. Если при любых разбиениях отрезка [a,b] таких, чтои при любом выборе точек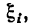 на отрезках [x_i-1,x_i] интегральная сумма

cтремится к одному и тому же пределу s, то этот предел называют определенным интегралом от функции f(x) на отрезке [a,b] и обозначают

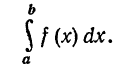
       ТАким образом, по определению

число а называется нижним пределом интеграла, b - верхним пределом интеграла. Отрезок [a,b] называется отрезком интегрирования,х - переменной интегрирования.
       О п р е д е л е н и е 2. Если для функции f(x) предел (6) существует, то функцию называют интегрируемой на отрезке [a,b].
       Заметим, что нижняя интегральная сумма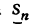 и верхняя интегральная сумма 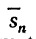являются частными случаями интегральной суммы (5), поэтому если f(x) интегрируема, то нижняя и верхняя интегральные суммы стремятсяк тому же пределу s, и поэтому на основании равенства (6) можем написать

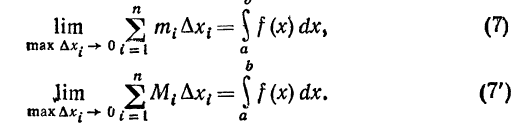
       Если построить график подынтегральной функции y=f(x), то в случае 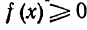интеграл

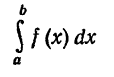
будет численно равен п л о щ а д и так называемой криволинейной трапеции, ограниченной указанной кривой, прямыми х=а, х=b и Осью Ох(рис. 214)

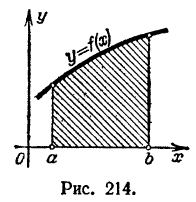
       Поэтому если требуется вычислить площадь криволинейной трапеции, ограниченной кривой y=f(x), прямыми х=а, х=b и Осью Ох, то эта площадь Q вычисляется с помощью интеграла:

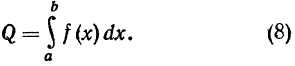
Докажем следующую важную теорему.
       Т е о р е м а 1. Если функция f(x) непрерывна на отрезке [a,b], то она интегрируется на этом отрезке.
       Д о к а з а т е л ь с т в о. Снова разобьем отрезок [a,b] (a < b) на отрезки [x0,x1],[x1,x2],...,[x_n-1,x_n]. Составим нижнюю и верхнюю интегральные суммы:

       Для дальнейшего установим некоторые свойства верхних и нижних интегральных сумм.
       С в о й с т в о 1.При увеличении числа отрезков, на которые мы разбиваем отрезок [а, b] путем добавления новых точек деления, нижняя интегральная сумма может только возрастать, а верхняя интегральная сумма только убывать.
       Д о к а з а т е л ь с т в о. Пусть отрезок [a,b] разбит на n' отрезков путем добавления новых точек (n' > n). Если какой-то отрезок [x_k-1,x_k] будет разбит на несколько отрезков, например, на p_k отрезков, то в новой нижней интегральной сумме отрезку [x_k-1,x_k] будет соответсвовать p_k слагаемых, которые мы обозначим через 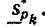В нижней интегральной сумме этому отрезку соответсвует одно слагаемоеНо для суммы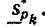 и величины справедливо неравенство, аналогичное неравенству (4) § 1. Мы можем написать

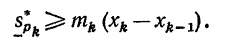
Написав соответствующие неравенства для каждого отрезка и суммируя левые и правые части получим

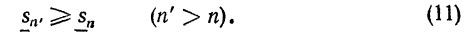
Свойство 1 доказано.
       С в о й с т в о 2. Нижняя интегрируемая сумма(9) и верхняя интегральная сумма(10) при неограниченом увеличении числа отрезков путем добавления новых точек деления стремятся к некоторым пределам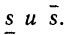
       Д о к а з а т е л ь с т в о. На основани неравенства (6) § 1. можем написать:

т.е. нижняя интегральная сумма ограничена при всех n. На основании свойств 1 нижняя интегральная сумма монотонно возрастает при возрастании n. Следовательно, но основании теоремы 7 о пределах эта переменная величина имеет предел;

Аналогично устанавливается, что верхняя интегральная сумма ограничена снизу и монотонно убывает. Следовательно она имеет предел:

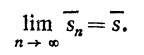
       С в о й с т в о 3. Если функция f(x) непрерывна на замкнутом отрезке [a,b], то пределы s и _s, определенные в свойстве 2 при условии, что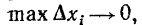равны
Этот общий предел обозначим через s:

       Д о к а з а т е л ь с т в о. Рассмотрим разность верхней и нижней интегральной суммы:

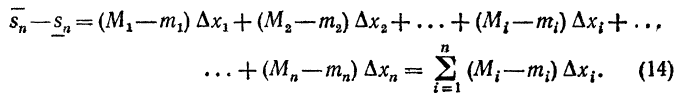
Обозначим через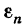 наибольшую из разностей M_i-m_i при даном разбиении:

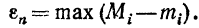
Можно доказать (на чем мы останавливатсья не будем), что если функция f(x) непрерывна на замкнутом отрезке, то при любом способе разбиения отрезка 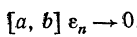,если только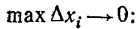

       Свойство непрерывной функции на замкнутом отрезке, выражаемое равенством (15), называется равномерной непрерывностью функции.
       Итак, мы будем пользоваться теоремой: Непрерывная функция на замкнутом отрезке равномерно непрерывна на этом отрезке.
Вернемся к равенству (14). Каждую разность M_i-m_i в правой части заменим не меньшей величиной 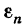Получаем неравенство

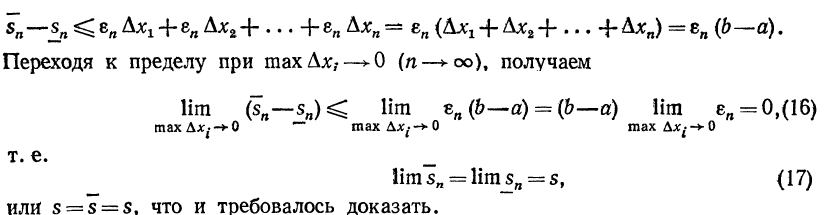
       С в о й с т в о 4.Пусть 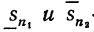- нижняя и верхняя интегральные суммы, соответствующие разбиениям отрезка [a,b]на n1 и cоответственно но n2 отрезков. Тогда имеет место неравенство

при любых n1 и n2.
       Д о к а з а т е л ь с т в о. Рассмотрим разбиение отрезка [a,b] на n3=n1+n2, отрезков, где точками деления будут точки деления первого и второго разбиений
На основании неравенства (3) § 1 имеем

На основании свойства 1 имеем

Пользуясь соотношениями (20) и (21), можно расширить неравенство (19):

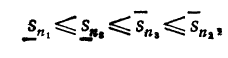
или

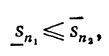
что и требовалось доказать.
       С в о й с т в о 5. Если функция f(x) непрерывна на отрезке [a,b], то при любой последовательности разбиений отрезка [a,b] на отрезки [x_i-1, x_i], не обязательно путем присоединения новых точек деления, если только max xi -> 0, нижняя интегральная сумма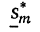 иверхняя интегральная сумма 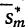стремятся к пределу s, определенному в свойстве 3.
       Д о к а з а т е л ь с т в о. Рассмотрим последовательность разбиений последовательности верхних интегралных сумм определенных в свойстве 2. При любых значениях n и m (на основании неравенства (18)) можем написать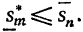
       Переходя к пределу при 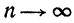на основании (15) можем написать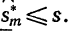
Аналогичным способом докажем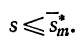
Итак,

или

Рассмотрим предел разности 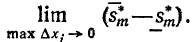Так как функция f(x) непрерывна на замкнутом отрезке [a,b]. то (так же как и при доказательстве свойства 3) докажем (см. равенство (16)), что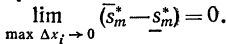
Перепишем последнее соотношение так:

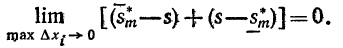
На основании (22) каждая из разностей, стоящих в квадратных скобках, неотрицательна. Следовательно,

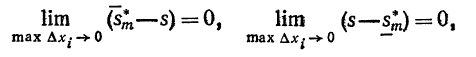
и окончательно получаем

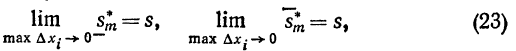
что и требовалось доказать.
       Теперь можно доказать и сформулированную выше теорему.
Пусть f(x) непрерывна на отрезке [a,b]. Рассмотрим произвольную последовательность интегральных сумм 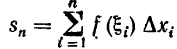такую, что 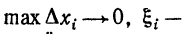произвольная точка отрезка [x_i-1, x_i].
       Для данной последовательности разбиений рассмотрим соответствующие последовательности верхних и нижних интегральных сумм _s_n и s_n. Для каждого разбиения будут справедливы соотношения (2):

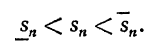
       Переходя к пределу при и пользуясь равенствами (23) получаем 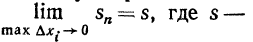предел, определенный в свойстве 3.
       Этот предел, как уже говорилось выше, и называется определенным интегралом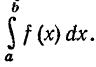Итак, если f(x) непрерывна на отрезке [a,b], то
       Отметим, что среди разрывных функций есть как интегрируемые, так и неинтегрируемые.
        З а м е ч а н и е 1. Отметим, что определенный интеграл зависит только от вида функции f(x) и пределов интегрирования, но не от переменной интегрирования, которую можно обозначить любой буквой:

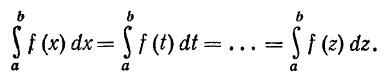
        З а м е ч а н и е 2. При введении понятия определенного интеграла мы предполагали, что a < b. В случае b > a примем п о   о п р е д е л е н и ю

Так например,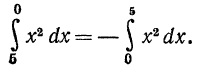
        З а м е ч а н и е 3. В случае a=b полагаем п о   о п р е д е л е н и ю, что для любой функции f(x) имеет место





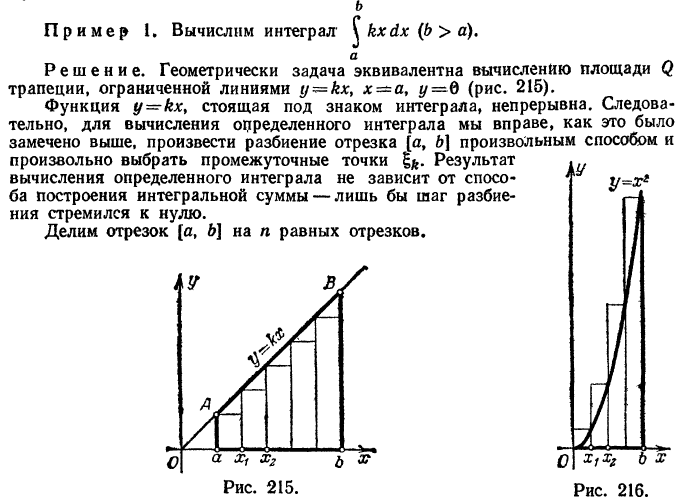
        З а м е ч а н и е 4.Только что рассмотренные примеры показывают, что непосредственное вычисление определенных интегралов как пределов интегральных сумм связано с большими трудностями. Даже в тех случаях, когда подынтегральные функции являются очень простыми (kxy x2, е*), этот способ требует громоздких подсчетов. Нахождение же определенных интегралов от более сложных функций приводит к еще большим трудностям. Поэтому естественно возникает задача: найти практически удобный метод вычисления определенных интегралов. Этот метод, открытый Ньютоном и Лейбницем, использует глубокую связь, существующую между интегрированием и дифференцированием. Изложению и обоснованию этого метода посвящены следующие параграфы настоящей главы.