|
9.1
Сущность и область применения гистограмм
Любому
закономерному
процессу в технике сопутствуют случайные отклонения. Конечные размеры
деталей,
химический состав сплавов, режимы термической обработки, характеристики
механических свойств материала и пр. имеют большие или меньшие
расхождения с
номинальными значениями. Анализ производственных ситуаций базируется на
данных,
полученных в результате контроля и измерения одного или нескольких
параметров
изделий, однако точно предсказать конечный результат отдельного
процесса или опыта
практически не возможно, так как он протекает каждый раз по-новому. Тем
не
менее, при многократном повторении обнаруживаются вполне определенные
закономерности, позволяющие прогнозировать исход большинства опытов.
Во всех без исключения
отраслях промышленности
требуется оценка точности и стабильности технологического процесса,
осуществление наблюдений за качеством продукции и отслеживание
различных
показателей производства. Производственные процессы в силу своей
сложности
подвержены воздействию многочисленных факторов, как внешних, так и
внутренних,
имеющих, как правило, случайную природу. Путем измерения параметров
соответствующими средствами получают ряд данных, представляющих собой
неупорядоченную
последовательность их случайных значений, на основе которых невозможно
сделать
корректные выводы.
Поэтому для
осмысления статистической информации о качестве часто строят гистограмму
распределения.
- ГИСТОГРАММА
- столбиковый график, являющийся графическим представлением
количественной информации в виде данных, сгруппированных по частоте
попадания в определенный, заранее заданный интервал.
- Это
инструмент оценки изменчивости исследуемого параметра, позволяющий
установить с заданной вероятностью действительное значение параметра и
оценить степень разброса измеренных значений относительно этого
значения.
- Она – не самоцель, а
оперативное средство обнаружения закономерностей воздействия на
исследуемый параметр отдельных факторов.
- Благодаря
внешнему виду, гистограмма помогает выявить структуру и характер
изменения данных, которые трудно заметить при их табличном
представлении.
- Гистограмму строят по результатам
измерений объектов в случайной выборке из всей совокупности объектов,
однако эти результаты позволяют судить о совокупности в целом.
- Ее
можно построить по данным, характеризующим не только
исчисляемую, но и не штучную продукцию, а также любой
процесс.
Гистограмма
дает много полезной информации о точности и стабильности
технологических
процессов, о возможностях оборудования и оснастки. Благодаря простоте
построения и наглядности гистограммы нашли применение в самых разных
областях.
Она используется для анализа:
· дефектности продукции;
· стабильности параметров качества
(размеров, массы, механических характеристик, химического состава,
выхода
продукции и др.) при контроле готовой продукции, при входном и
приемочном
контроле;
· качества услуг;
· возможностей технологических
процессов;
· качества работы отдельных
исполнителей, станков
и т.д.;
· корректности принимаемых
решений.
9.2 Основные понятия и определения
математической
статистики
9.2.1
Статистическая природа материального мира
Статистические методы УК
базируются на теории вероятностей и математической статистике.
Наверное,
поэтому многих пугает сложность математического аппарата, применяемого
в
статистике. Действительно,
статистический анализ
как раздел теории вероятностей
достаточно серьезен. Математическая статистика занимается как
статистическим
описанием результатов опытов или наблюдений, так и построением и
проверкой
подходящих математических моделей, содержащих понятие вероятности.
Ее
методы расширяют возможности научного предсказания и рационального
принятия
решения во многих задачах, где существенные параметры не могут быть
известны
или контролируемы с достаточной точностью. Статистические описания и
модели
применяются к физическим процессам, обладающим интересным специфическим
свойством: хотя результат отдельного измерения физической величины хi не
может быть предсказан с достаточной точностью, существует некая функция
у=у(х1,
х2, … хn) от
множества результатов хi повторных измерений,
значение которой может
быть предсказано с гораздо большей точностью. Это свойство процесса
называют статистической
устойчивостью. В каждом конкретном случае это свойство
выражает эмпирический
физический закон, который может быть проверен только опытом. Точность
такого
предсказания возрастает с ростом объема n выборки
значений хi.
Однако, учитывая
потребности производства,
были разработаны, в том числе и российскими учеными, простейшие методы
статистического анализа, пригодные для целей управления качеством на уровне, приемлемом даже
для
квалифицированного рабочего.
Здесь даются
лишь некоторые основные положения теории вероятностей и математической
статистики, необходимые для понимания методов статистического анализа и
управления процессами. Более полные и обстоятельные сведения по этой
тематике
можно найти в капитальных работах [4, 5].
9.2.2
Событие и его вероятность
Событие
является
результатом любого опыта (испытания) проводимого в заданных условиях
является.
Оно может иметь качественную или количественную характеристику.
Качественной
характеристикой события может быть, например изготовление качественной
или
некачественной детали, а количественной характеристикой –
случайная величина ее
размера.
Событие,
которое в результате данного опыта должно обязательно произойти
называют достоверным,
а то, которое в данных условиях не произойдет
никогда, называют невозможным.
Если в опыте событие может произойти, а может и
не произойти, его называют случайным событием.
Классическим
примером случайного события является извлечение белого шара из ящика с
белыми и
черными шарами.
Вероятность
Р(A)
– средняя
частота появления случайного события А при многократной (в пределе
–
бесконечной) реализации условий для его наблюдения. Абсолютно
достоверные
события имеют Р(A) = 1, невозможные
– Р(A) = 0, для
произвольного
события 0<=Р(A)<=1. Вероятность
наблюдения
случайного события является его важнейшей характеристикой.
В
большинстве
случаев вероятность события не может быть найдена аналитически, ее
оценивают на
основании результатов опытов с помощью накопленной частоты
случайного
события W(А)
– отношения числа опытов i,
в которых появилось событие А, к общему числу проделанных опытов n, т.е. W(А)=i/n. Повторяя
серию из n
опытов многократно, будем
получать различные значения W(А),
однако, близкие к вероятности Р(A)
появления этого события. При
этом, чем больше
будет проделано опытов,
тем ближе будет значение W(А)
к величине Р(A).
9.2.3
Случайная величина и законы ее распределения
Если под
событием понимать появление какого-либо числа, это число будет случайной
величиной.
Случайная
величина (стохастическая переменная) – величина,
наблюдаемое значение
которой зависит от случайных причин.
Случайная
величина является количественной характеристикой результата опыта и
может
принимать различные числовые значения, заранее неизвестные и зависящие
от
случайных причин, которые не могут быть полностью учтены. Случайная
величина
характеризуется вероятностью, с которой она может приобрести то или
иное
значение из генеральной совокупности в области
допустимых значений.
Генеральная
совокупность –
полный набор всех возможных значений случайной величины А. Она
может быть
или непрерывной средой, или набором дискретных значений. В статистике
под генеральной
совокупностью понимают все множество исследуемых
объектов. Совокупность
однородна, если хотя бы один ее существенный признак
является
общим для всех объектов совокупности.
Признак
– качественная особенность объекта, принадлежащего данной совокупности.
Признаки могут быть количественными
и атрибутивными (качественными).
Наиболее
полно
случайные величины* могут быть охарактеризованы с помощью интегральной
функции
распределения F(x), представляющей
собой
вероятность появления значения X, не превышающего
x,
т.е.
Р(Х <
х) = F(х).
Функция
распределения F(х) является
неубывающей функцией Х (рисунок
9.1а). Вероятность попадания величины Х в интервал
х1 <
Х
£
х2 равна
Р(х1
<
Х £
х2) = F(х2)
- F(х1).
Функция F(х)
удовлетворяет
условиям F(-¥)
= 0
и F(¥)
=
1.
Для
непрерывных, случайных величин F(х) имеет
производную, которая называется функцией
плотности вероятности
j(х) =
dF(х)/dх. Плотность
вероятности удовлетворяет
условию j(х)
³
0 (рисунок 9.1б).
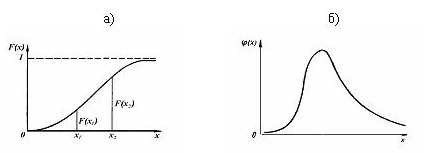
Рисунок 9.1 –
Интегральная функция распределения (а) и функция плотности вероятности
(б)
случайной величины
Вероятность
попадания случайной величины Х в интервал х1
< Х <
х2 может
быть найдена
через плотность вероятности Р(х1 <
Х < х2)=
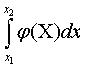 . .
Функция
распределения данной случайной величины связана с ее плотностью
вероятности
соотношением F(x) = 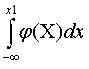 ,
поэтому площадь под кривой равна единице, т.е. ,
поэтому площадь под кривой равна единице, т.е.
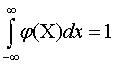
----------------
* Случайные
величины будем обозначать прописными латинскими буквами, а их возможные
значения – соответствующими строчными.
9.2.4
Числовые характеристики непрерывных случайных величин
9.2.4.1
Характеристики центра распределения
В
практических
случаях вместо задания функций распределения случайной величины бывает
достаточно указать некоторые их числовые характеристики, называемые статистиками.
В качестве
числовых характеристик положения центра группирования случайных величин
используют математическое ожидание а
(для генеральной
совокупности) или среднее арифметическое значение 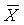 (для группы
случайных величин),. (для группы
случайных величин),.
Математическое
ожидание определяют
как
а=
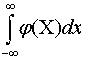
Это
–
основная, но не единственная характеристика центра группирования.
Другими его
характеристиками являются мода (Мо) и медиана (Ме).
Модой
величины Х является такое значение МоХ,
в котором плотность
вероятности имеет максимальное значение (рисунок 9.2а).
Медианой
величины Х служит значение МеХ,
которое соответствует
условию
Р(Х < МеХ) = Р(Х > МеХ) = 0,5.
Геометрически
медиана это
абсцисса прямой, которая делит площадь, ограниченную кривой плотности
вероятности, пополам (рисунок 9.2б).
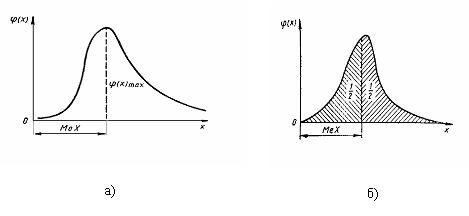
Рисунок
9.2 – Мода (а) и медиана (б) распределения случайной
величины
Для
симметричных распределений характерно совпадение значений средней
арифметической, моды и медианы. Если Мо >  ,
то ряд будет иметь левостороннюю асимметрию,
если Мо < ,
то ряд будет иметь левостороннюю асимметрию,
если Мо <  - правостороннюю. В умеренно асимметричных
рядах соотношение
между указанными показателями выражается следующим образом. - правостороннюю. В умеренно асимметричных
рядах соотношение
между указанными показателями выражается следующим образом.
9.2.4.2
Характеристики рассеивания
Одной из
основных характеристик рассеивания случайной величины Х около центра
распределения служит дисперсия, которая
обозначается s2
и
определяется по формуле s2
= 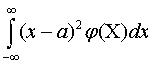
Часто в
качестве меры рассеивания случайной величины вместо дисперсии
используют
положительное значение квадратного корня из дисперсии, которое
называется средним
квадратическим отклонением или стандартным
отклонением
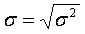 В практике
широко применяют также характеристику рассеивания, называемую коэффициентом
вариации, представляющим собой отношение среднего
квадратического
отклонения к математическому ожиданию
g = (s/
а) ´100%
Коэффициент
вариации показывает, насколько велико рассеивание по сравнению со
средним
значением случайной величины.
9.2.4.3
Моменты распределения
Начальным
моментом распределения k
–го порядка hk называется
число, определяемое по формуле
hk
= 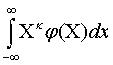
Центральный
момент k
-го
порядка mk определяется из
выражения mk = 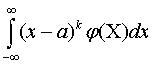
Для
статистической обработки результатов используют моменты первых четырех
порядков. Между начальными и центральными моментами распределения
существуют
следующие зависимости
m1 = 0
m2 = h2
– h12
m3 = h3
– 3h2h1
+ 2h12 ;
m4 = h4
– 4h3h1
+ 6h2h12
– 3h14.
Здесь: h1
= а;
m2=
s2
.
Третий
центральный момент m3
используют для вычисления показателя асимметрии
распределения Sk
= m3/s3.
Четвертый
центральный момент m4
применяют для определения показателя эксцесса
Еk = (m4/s4)–3,
являющегося характеристикой крутизны распределения. Отличные от нуля
показатели
асимметрии и эксцесса указывают на отклонение рассматриваемого
распределения от
нормального.
9.2.4.4
Понятие о выборке. Эмпирическое распределение случайной величины.
Доверительный
интервал
Любые
результаты измерения характеристик объекта получают, проводя
ограниченное число
опытов, поэтому полученные значения всегда в разной степени отличаются
от так
называемых генеральных характеристик, которые
могли бы быть определены
по результатам бесконечно
большого числа измерений, образующих генеральную совокупность. Реально
полученная,
ограниченная часть этой совокупности называется выборочной совокупностью
(выборкой).
Выборка
– часть объектов генеральной совокупности, выделенная для
изучения.
Сформировать
выборку – сложная задача. Основные требования к выборке:
-
равные шансы
попасть в выборку для всех объектов
генеральной совокупности;
-
извлечение выборки
из генеральной совокупности –
случайным образом.
-
представительность
(репрезентативность) выборки.
Формируют
выборку по таблицам случайных чисел или на ЭВМ с помощью генератора
псевдослучайных чисел.
Разница между выборочными
и генеральными
значениями характеристик
уменьшается с
увеличением объема выборки, т.е. вероятность события, состоящего в том,
что
разница между указанными значениями характеристик не будет превышать
сколь
угодно малую величину, при увеличении объема выборки неограниченно
приближается
к единице.
При
малом объеме выборки (n <
40 ¸
60)
выборочное среднее значение характеристики
определяют как 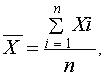
где Xi — единичное
значение
признака; п —
число наблюдений
(число значений признака). Эта средняя используется тогда, когда каждое значение признака
встречается только
один раз или они равны между собой.
В этом случае
мода – это наиболее
часто
встречающееся в выборке значение признака. Для дискретного
ряда она
определяется непосредственно как вариант х,
имеющий
наибольшую частоту.
Медиана - значение признака у средней
единицы ранжированного ряда.
Для ее
нахождения сначала
определяется
ее порядковый номер ,
а затем по накопленным частотам определяется сама медиана.
Выборочная
дисперсия характеристики
определяется как
S2 = 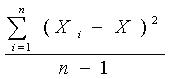
Выборочное
среднее квадратическое отклонение и
выборочный коэффициент вариации определяют соответственно как 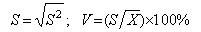
При
большом объеме выборки (n > 60)
значения
измеренных характеристик систематизируют в виде вариационного ряда,
разбивают
на несколько интервалов и подсчитывают число значений, попавших в
каждый
интервал (частоту попадания в интервал).
Если частоты
отличны друг от друга, расчет производится по формуле взвешенной средней арифметической
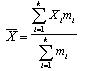 где Xi — центральное значение i-го интервала; тi
— частота попадания замеров в заданный интервал; k - число интервалов.
Для
интервального ряда с равными интервалами мода
рассчитывается по формуле
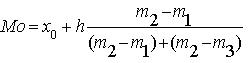
где x0
– нижняя граница модального
интервала; h
- ширина интервала;
m2
-
частота модального интервала; m1
- частота интервала,
предшествующего модальному; m3 -
частота интервала, следующего за модальным.
В ряду с
неравными
интервалами мода определяется в интервале, имеющем наибольшую плотность
распределения, и в
формуле вместо m1,
m2,
m3
принимаются
соответствующие плотности распределения.
Медианный интервал в этом случае определяется простой интерполяцией.
Значение медианы рассчитывается по формуле
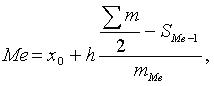 где x0
- нижняя граница медианного интервала; порядковый
номер медианы; SMe-1-
накопленная частота до медианного интервала; mMe-
частота медианного интервала.
Продемонстрируем
расчет выборочных моды и медианы на простом примере.
Пример.
Требуется определить моду и медиану по выборочным данным о заработной
плате
рабочих одного из цехов предприятия.
Таблица 9.1
-
Сведения о заработной плате рабочих цеха № 10
| Месячная
заработная плата, тыс. руб. | 4-5
| 5-6
| 6-7
| 7-8
| 8-9
| 9-10
| Итого
(накопленная частота) |
| Число
рабочих | 10
| 20
| 48
| 60
| 42
| 20
| 200
|
Значение
медианы, равное 7367 руб. говорит о том,
что половина рабочих получает заработную плату ниже этой суммы, а
половина — выше.
Мода и медиана могут
быть определены также:
первая - по гистограмме, а вторая по кумуляте
(рисунок 9.3).
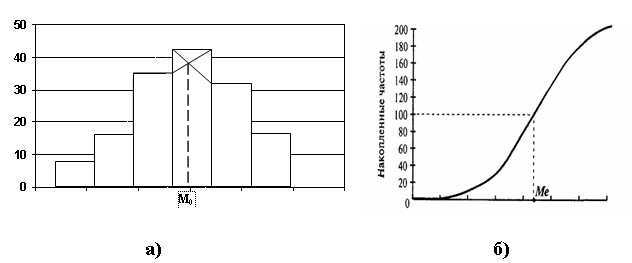
Рисунок 9.3 -
Гистограмма (а) и кумулята (б) распределения двухсот рабочих по уровню
заработной платы.
Для интервального ряда взвешенную
дисперсию
определяют из выражения
Определение
выборочного среднего квадратического
отклонения и коэффициента вариации в этом случае ничем не отличается от
предыдущего.
Если
необходимо определить показатели асимметрии и
эксцесса выборочного распределения, предварительно находят начальные
моменты распределения: 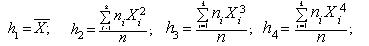
Затем
определяют центральные моменты m3
и m4,
и после этого находят значения Sk
= m3/s3
и Еk
= (m4/s4)–3
(см.
выше).
Формулы
расчета выборочных характеристик могут быть использованы как для
непрерывных,
так и для дискретных случайных величин.
На практике
обычно выборочными характеристиками
оценивают величины генеральных характеристик. Оценка может
быть точечной
(одно число) или интервальной.
Характеристикой
неопределенности случайной величины, исследуемой по выборке, является
Доверительный
интервал – интервал значений признака Х, в котором
с заданной вероятностью
находится значение
исследуемой величины:
x-
D
< X
< x+D
,
где Х
–
значение признака генеральной совокупности; х – выборочное
значение признака; D -
предельная ошибка выборки.
Ширина
доверительного интервала определяется принятым уровнем доверительной
вероятности. На практике чаще всего используют Р = 0,9; 0,95;
0,99.
Уровнем
значимости называют
величину a
= 1
– Р. Соответственно, наиболее употребительными его
значениями являются
a
= 0,1; 0,05; 0,001.
9.2.4.5
Проверка статистической гипотезы
Статистическая
гипотеза – это предположение о свойствах изучаемой величины. В
отношении
качества это предположение связывается с нормами на значения величин,
характеризующих качество. С помощью статистических критериев проверяют
т.н. нулевую
гипотезу Н0 в отношении выборочного
значения Q0 и значения
генеральной совокупности Q (Q0 отражает
Q).
В
статистическом анализе возможны ошибки двух видов:
- ошибка
1-го рода (a)
– отклоняется верная гипотеза;
-
ошибка
2-го рода (b)
– принимается ложная гипотеза.
Применительно
к производству продукции ошибка 1-го рода может быть совершена, если
при контроле
качества будет ошибочно забракована партия годных изделий. Вероятность
совершить такую ошибку называют альфа-риском
или риском
поставщика. В управлении процессами – это
ложное выявление нарушения
процесса при его
фактическом
отсутствии. Результат этой ошибки – затраты, связанные с
излишней борьбой с
несуществующей проблемой. Ошибка 2-го рода – пропуск
бракованной партии
изделий. Вероятность такой ошибки называют бета-риском
или риском
потребителя. В управлении процессами –
это необнаружение фактически произошедшего
нарушения процесса. Результат такой ошибки
– потери, связанные с
производством брака и последствиями его устранения. При этом упускается
возможность установить причины нарушения. 9.2.4.6
Нормальный закон распределения
В
зависимости
от характера случайной величины законы ее распределения могут быть
самыми
различными. Если на исследуемую величину одновременно действует много
независимых случайных факторов, она подчиняется нормальному
закону
распределения (закону Гаусса). Этот закон имеет
фундаментальное значение.
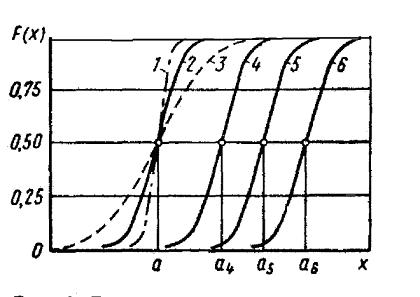
Рисунок
9.4 -
Графики функций нормального распределения для
различных значений а и
s2
: 1,2,3 – а1 = а2
= а3 = а ;
s21
<
s22
<
s23
; 2,4,5,6 – а2
< а4 <а5 <
а6 ; s22
= s24
= s25
= s26
Нормальная
плотность вероятности определяется выражением
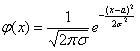 . .
На рисунке
9.5
приведены графики нормальной плотности вероятностей для различных
значений а
и s2.
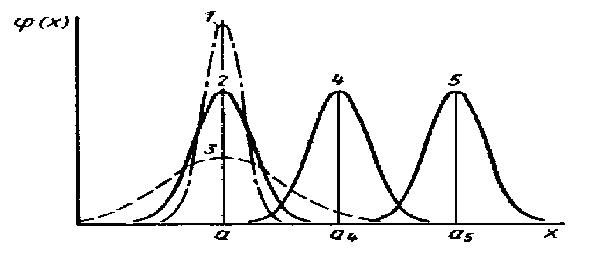 Рисунок 9.5 - Графики нормальной
плотности вероятностей для различных
значений а и
s2
: 1,2,3 – а1 = а2
= а3 = а ; s21
<
s22
<
s23
; 2,4,5 – а2
< а4 <а5 ;
s22
= s24
= s25 Рисунок 9.5 - Графики нормальной
плотности вероятностей для различных
значений а и
s2
: 1,2,3 – а1 = а2
= а3 = а ; s21
<
s22
<
s23
; 2,4,5 – а2
< а4 <а5 ;
s22
= s24
= s25
9.3
Ппостроение гистограммы
Гистограмма
строится в
следующем порядке.
Методика
построения
1.
Формируют выборку, т.е. собирают исходные данные за определенный период
времени. Количество значений признака не менее 30, оптимальное
количество –
100.
2.
Определяют выборочный размах:
R = хmax - xmin
(разница между
наибольшим и наименьшим наблюдаемыми значениями).
3. Делят
размах на
интервалы равной ширины.
Ширину интервалов находят как 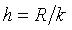 .
Количество интервалов k зависит от
объема выборки n: .
Количество интервалов k зависит от
объема выборки n:
| Объем выборки n
| 20 –
50
| 51 –
100
| 101 –
200
| 201 –
500
| 501 –
1000
| более 1000
| | Число интервалов k
| 6 |
7 |
8 |
9 |
10 |
11 - 20 |
Для
определения количества интервалов при n>300…500 можно
использовать формулу Стержерса: 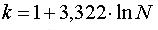 , где N - генеральная совокупность. , где N - генеральная совокупность.
4.
Определяют границы
интервалов:
- определяют левую границу
первого интервала (<хьшт);
- прибавляют
к ней ширину интервала, чтобы получить
его правую границу;
- к
правой границе последовательно прибавляют ширину интервала для получения
второй, третьей и
т.д. правых границ;
- проверяют,
что хmax
входит в последний интервал;
5. Вычисляют середины интервалов как
полусуммы их левых и правых границ.
6.
Определяют частоты попадания значений в каждый интервал. Значения,
совпадающие с правой границей, относят к левому интервалу. Готовят таблицу частот, куда
заносят
интервалы, их средние значения, частоты попадания в интервал.
7. Строят столбчатый график
гистограммы, где на
оси абсцисс откладывают значения исследуемого показателя, а на оси
ординат –
частоты попадания измеренных значений в интервал
Возможные
варианты
расположения гистограммы относительно поля допуска и соответствующие им
состояния процесса приведены в прил. В.
Таким
образом, анализ процесса с помощью
гистограмм позволяет установить, находится ли процесс в данный момент
в статистически управляемом состоянии. Только в
этом случае можно начинать анализ факторов, влияющих на его протекание,
и
корректирующие воздействия, направленные на его улучшение.
|