В процессе производства и при анализе его результатов часто приходится выяснять, существует ли зависимость между двумя различными параметрами процесса. Например, зависит ли точность размеров детали от скорости вращения шпинделя токарного станка? Или можно ли контролировать концентрацию определенного вещества в материале, измеряя  удельный вес последнего, поскольку сделать это проще? Или  зависит ли качество собранного изделия от качества комплектующих его деталей и узлов? Для ответов на эти вопросы, т.е. для выявления зависимости между отдельными факторами производства используют т.н. диаграммы разброса (рассеивания), которые также называют полем корреляции.

ДИАГРАММА РАЗБРОСА – ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ВЗАИМОСВЯЗИ МЕЖДУ ДВУМЯ ПЕРЕМЕННЫМИ ВЕЛИЧИНАМИ.

Диаграмма разброса - инструмент, позволяющий выявить  наличие и определить вид и тесноту связи между двумя случайно изменяющимися факторами.

При построении диаграмм разброса рекомендуется следующее:

  - для выбора диапазонов значений X и Y на осях диаграммы выберите в таблице исходных данных минимальное и максимальное значения каждой величины (смотри таблицу 8.1);

 - шкалы на осях подбирайте таким образом, чтобы исследуемые диапазоны изменения  аргумента Х (горизонтальная ось)  и функции Y (вертикальная ось) на графике были примерно равны, тогда диаграмму будет легче читать;

- каждую ось разбивайте на 5-10 участков (делений) со значениями, кратными 1, 2, 5, 10;

- для больших и малых значений величин  используйте общеупотребимые кратные и дольные приставки к обозначениям единиц их измерения или укажите после обозначения величин у концов осей множитель вида 10ⁿ, на который надо умножить действительное значение переменной, чтобы получить значение, указанное на шкале;

- для одинаковых значений, полученных в разных наблюдениях, точки  либо наносите  концентрическими кружками, либо располагайте рядом;

- при необходимости нанести на один график два массива однотипных данных, отличающихся третьим параметром, используйте значки разной формы с обязательной их расшифровкой на диаграмме.

Применительно к анализу качества диаграмму разброса можно построить между:

-  характеристикой качества и влияющим на нее фактором;

-  двумя различными характеристиками качества;

-  двумя факторами, влияющими на одну  характеристику качества.

Ниже дан пример таблицы с исходными данными измерений.

Таблица 8.1 – Исходные данные для построения диаграммы разброса

Испытательная лаборатория: ТС456 .  Инж.-испытатель:  Петров И.И.

Объект: Вольтметр В7-22.                     Дата: 1.9.01.   

                Данные испытаний на электрическую прочность изоляции токоведущих частей

                при различной влажности окружающей среды

RH (Х) – относительная влажность, %;    V (У)– напряжение пробоя изоляции, кВ.

Пример диаграммы разброса, построенной по данным таблицы, представлен на рисунке 8.1.

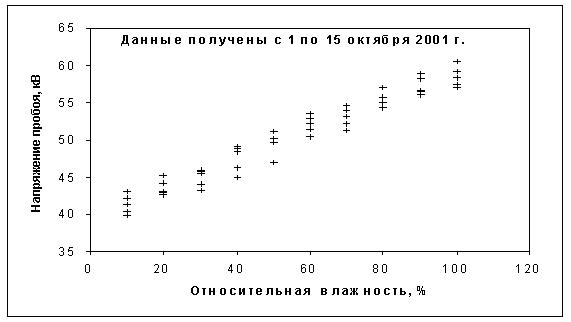
Рисунок 8.1 – Зависимость напряжения пробоя изоляции от влажности

Существуют различные оценки степени (тесноты) корреляционной зависимости. Одной из них является коэффициент корреляции r :

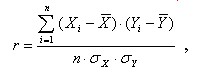(1)

где  n - число пар исследуемых параметров ;X, Y, s_X, s_Y - средние значения и средние квадратические отклонения этих параметров  соответственно.

Для удобства расчета коэффициента корреляции можно использовать формулу

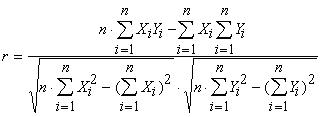
где X, Y —- значения параметров Х и Y для i-го измерения; ,  — средние арифметические значения величин Х и Y; п — число измерений в выборке (объем выборки).

Если r=±1, это свидетельствует о наличии абсолютной корреляционной зависимости, если r=0, корреляционная зависимость отсутствует. Однако для случайных величин такие значения r получить практически не возможно. Чем ближе коэффициент корреляции к единице, тем теснее зависимость между параметрами.

Принято считать, что корреляционная связь:

при 0 < r =< |0,3| - слабая,

при |0,3| <  r =< |0,7| - средняя,

при |0,7| < r  =< |0,9| - сильная,

при |0,9|< r < 1 - весьма сильная.

Наличие корреляционной зависимости между двумя параметрами процесса дает возможность управлять последним, контролируя другой параметр и зная характер корреляционной связи между ними. Это существенно расширяет возможности управления, однако требует дополнительных исследований для установления наличия, степени и вида корреляции.

Различают три основных вида корреляции: положительную, отрицательную и сложную.

При положительной с увеличением Х увеличивается Y.

При отрицательной с увеличением Х уменьшается Y.

При сложной с увеличением Х изменение Y неоднозначно.

Простейшей формой положительной или отрицательной корреляции является линейная зависимость, прямая или обратная соответственно (рисунок 8.2а и б соответственно). На рисунках 8.2в и г эти же корреляционные связи выражены слабее. Более сложные, наиболее распространенные формы – нелинейные (степенная, экспоненциальная, логарифмическая и др.). При наличии качественных изменений процесса, характеризуемого значением Y в диапазоне варьирования Х, на диаграмме разброса могут наблюдаться переломы или разрывы. Формы сложной корреляции чрезвычайно разнообразны. Пример диаграммы такой зависимости представлен на рисунке 8.2д. Такие диаграммы могут содержать участки линейной и нелинейной корреляции. В этом случае диапазон варьирования Х делят на отдельные участки и исследуют зависимости раздельно.

Пример диаграммы, демонстрирующей отсутствие корреляции (r=0) приведен на рисунке 8.2е и 8.3.

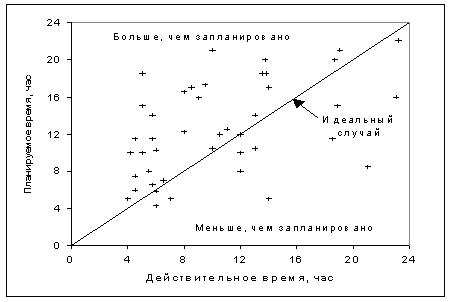
Рисунок 8.3 - Анализ времени выполнения технического обслуживания

Зависимости между параметрами не наблюдается, хотя разбивка диаграммы на две области облегчает анализ исследуемых несоответствия параметров.

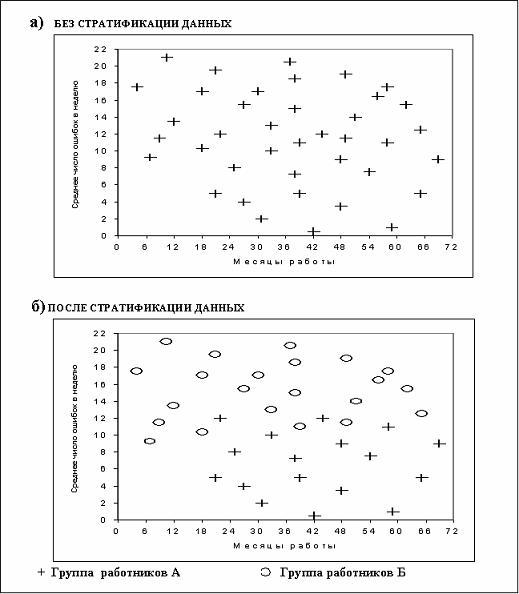
Рисунок 8.4 - Анализ ошибок работников страховой компании

за период с 1.01.2001 г. по 30.06.2002 г.

Стратификация позволила предположить, что группа работников А работает значительно качественнее. Однако, для того, чтобы это предположение стало фактом, необходимо провести статистический анализ данных по каждой группе отдельно, вычислить доверительные интервалы для заданной вероятности и убедиться, что они не накладываются друг на друга. В то же время, очевидно, что в течение данного периода существенного изменения качества работы в ту или другую сторону ни в одной из групп не наблюдалось.