| Основные типы передач зацеплением.
Особенности зубчатых передач.
Зубчатые передачи обладают рядом существенных достоинств: имеют относительно малые габариты (достаточная компактность), в любой момент передаточное отношение поддерживается постоянным (круглые колеса) или изменяется по заданной зависимости (некруглые колеса), КПД достаточно высок, надежность работы, большая долговечность, простота ухода и обслуживания.
В машиностроении и приборостроении применяют зубчатые передачи с цилиндрическими колесами с прямыми и косыми зубьями (Рис. 1. а,б), конические колеса с прямыми, косыми и криволинейными зубьями (Рис. 1. в - д) для передачи мощности от ведущего вала к ведомому с преобразованием передаваемых скоростей и моментов. Основное назначение зубчатых механизмов в приборах – преобразование скорости и изменение направления вращения.
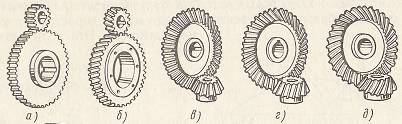
Рис. 1.
Простейшая зубчатая передача (Рис. 2, а) представляет собой трехзвенный механизм, состоящий из колес 1 и 2 с нарезанными на них зубьями и корпуса (стойки) 3. Меньшее колесо обычно называют шестерней (в приборах - трибом). При вращении колес относительно своих геометрических осей окружности диаметров dw1 и dw2 катятся одна по другой без скольжения, что является отличительной особенностью зубчатых передач. Эти окружности называются начальными.
По взаимному расположению осей зубчатые передачи разделяются на цилиндрические – с параллельными осями (Рис. 2, а, б, в, г) и конические – с пересекающимися осями (Рис. 2, д).
Рис. 2
Цилиндрические механизмы выполняют с внешним (Рис. 3,а) или внутренним (Рис. 3,в) зацеплением. Внутреннее зацепление позволяет уменьшить габаритные размеры механизма, однако технологически более сложно. Кроме того, при внутреннем зацеплении один из валов воспринимает консольную нагрузку и работает в более сложных условиях. Цилиндрические зубчатые колеса могут иметь прямые или косые зубья.
Рис. 3
Механизмы с прямыми зубьями (Рис.3,а) применяют в сравнительно тихоходных передачах при малых динамических нагрузках. Основным преимуществом этих механизмов является отсутствие осевых усилий, благодаря чему имеется возможность передвижения колес вдоль оси во время работы. Недостаточная плавность прямозубого зацепления приводит к появлению шума в процессе работы. Для устранения этого недостатка применяют косозубые цилиндрические механизмы (Рис. 3,б), имеющие повышенную прочность зубьев и большую плавность зацепления. Поэтому они могут работать при высоких скоростях и динамических нагрузках. Недостаток этих передач – наличие осевых усилий, действующих на колеса и подшипниковые узлы.
Параметры прямозубых цилиндрических колес.
На рис. 4 представлено зацепление двух прямозубых цилиндрических колец. Начальные окружности шестерни 1 и колеса 2 при вращении катятся одна по другой без скольжения. Внешняя окружность зубчатого колеса, очерчивающего вершины зубьев называется окружностью вершин, а окружность, ограничивающая основания впадин, называется окружностью впадин. Очертание зуба в плоскости поперечного сечения принято называть профилем зуба. Как показано на рис. 4 пара зубчатых колес собирается с радиальным зазором между окружностями вершин одного колеса и впадин другого. Этот зазор нужен для того, чтобы зуб не заклинился во впадине, а также для компенсации температурных деформаций и ошибок изготовления и сборки. Для этих целей установлен стандартами определенный боковой зазор между соседними зубьями, который получается вследствие отрицательных допусков на толщину зубьев. При геометрических же расчетах зубчатой передачи боковой зазор принимается равным нулю. Закругленный переход боковой поверхности зуба в окружность впадин получил название галтели.
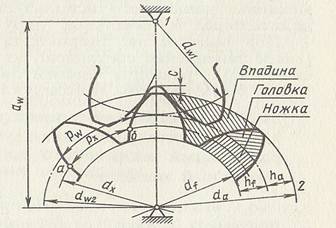
Рис. 4
Расстояние между соответствующими точками двух соседних зубьев, измеренное по начальной окружности
диаметра, называется начальным шагом. Модуль зацепления m, измеряемый в мм, - основной параметр зубчатого зацепления, с помощью которого определяют размеры передачи. Модуль может назначаться исходя из технологических и конструктивных условий, а в передачах со значительными силовыми нагрузками.
Геометрические элементы.
Стандартным значение модуля будет лишь для одной окружности, которая называется делительной. Элемент зуба, расположенный с внешней стороны делительной окружности, называется делительной головкой зуба, а с внутренней стороны этой окружности – делительной ножкой зуба. В точной механике чаще всего используется зацепление колес, в котором делительные и начальные окружности совпадают.
Размеры элементов шестерни и зубчатого колеса могут быть найдены по следующим зависимостям:
высота делительной головки зуба 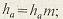
высота делительной ножки зуба 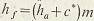
радиальный зазор 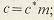
начальный диаметр
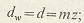
диаметры вершин и впадин
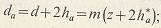
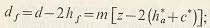
радиус галтели
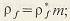
межосевое расстояние
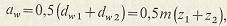
где 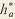 - коэффициент высоты головки зуба (для нормальных зубьев - коэффициент высоты головки зуба (для нормальных зубьев 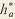 = 1, для укороченных = 1, для укороченных 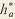 = 0.8); = 0.8); 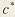 - коэффициент радиального зазора (если - коэффициент радиального зазора (если 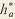 = 1, то для = 1, то для 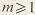 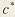 = 0.25; для = 0.25; для 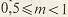 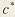 = 0.35; для = 0.35; для 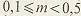 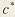 = 0.4); коэффициент = 0.4); коэффициент 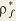 равен 0,384 при равен 0,384 при 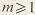 , 0,38…0,44 при , 0,38…0,44 при 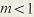 . .
Основная теорема зацепления.
Условие нормальной работы зубчатой передачи с круглыми колесами – обеспечение постоянного передаточного отношения. Передаточное отношение, в свою очередь, является основной кинематической характеристикой зубчатого механизма, равное отношению угловой скорости ведущего зубчатого колеса к угловой скорости ведомого колеса.
Суть основной теоремы зацепления состоит в том, что для обеспечения уровня i=const сопряженные профили зубьев должны быть очерчены такими кривыми, у которых нормаль NN в любой точке С взаимного касания зубьев (Рис. 5,а) всегда проходит через постоянную точку Р на линии центров колес О1О2 (через полюс зацепления), т.о. линия действия одного профиля на другой делит линию центров на части, обратно пропорциональные их угловым скоростям. В основной теореме зубья рассматриваются как абсолютно жесткие, т.е. их деформации не учитываются. Для малонагруженных передач деформации зубьев меньше погрешностей изготовления и требования теоремы полностью отвечают практике.
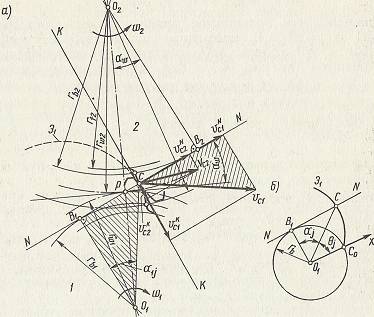
Рис. 5
Геометрический расчет.
Основные параметры зубчатых колес и передачи определяют по модулю и числу зубьев.
Для цилиндрических прямозубых колес диаметр делительной окружности 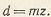
Для колес наружного зацепления, нарезанных без смещения зуборезного инструмента, когда делительная окружность колеса катится без скольжения по средней линии профиля инструмента, диаметр окружности вершин зубьев:
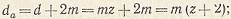
диаметр окружности впадин
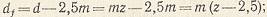
межцентровое расстояние 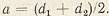 Выражая диаметры делительных окружностей через модуль и число зубьев, получим Выражая диаметры делительных окружностей через модуль и число зубьев, получим
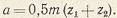
Толщина зуба по делительной окружности (без учета бокового зазора):
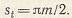
Силовой расчет.
В процессе работы зубчатой передачи в зацеплении действует нормальная сила Fn, направленная по линии зацепления (Рис. 6). При расчете валов, опор вращения и корпусов удобно силу Fn представить в виде трех ортогональных компонент: Ft – окружной силы (Ft = Fncosα), Fα – осевой силы, Fr – радиальной силы (Fr =Fnsinα или Fr = Ft tgα). Действие силы Fn приводит к возникновению в зубе сложного напряженного состояния.
При проектировании передач обычно задают значение Т2, и по нему определяют:
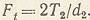
Если задан движущий момент Т1, то
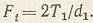
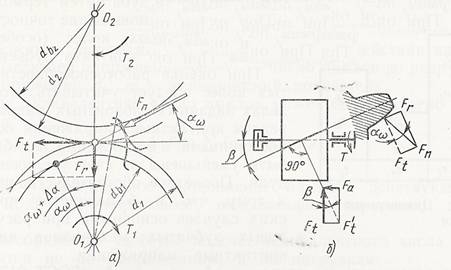
Рис.6.
Давление между рабочими поверхностями зубьев передается по общей нормали к их профилям (Рис. 7,а). Если к ведомому колесу 2 приложен момент сопротивления Т2, то условная сосредоточенная сила давления зуба шестерни 1 на зуб колеса 2
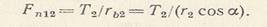
Так как действие равно противодействию, то сила давления зуба колеса 2 на зуб шестерни 1
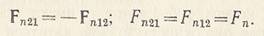
Рис. 7
Необходимый вращающий момент на ведущем валу (без учета потерь)

откуда
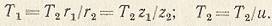
С учетом потерь 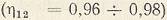 получим получим
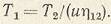
Косозубые цилиндрические передачи.
Косозубые цилиндрические передачи отличаются от прямозубых тем, что оси их зубьев составляет некоторый угол β с осью колеса (Рис. 8,а) Благодаря косому расположению длина зуба больше длины колеса, т.е. контактные напряжения уменьшаются по сравнению с прямозубыми колесами. Косозубые передачи обеспечивают более плавный и бесшумный ход, допускают более высокие нагрузки и скорости. Кроме того, косозубые передачи дают возможность получить строго определенное межосевое расстояние путем выбора соответствующего угла наклона линии зуба β.
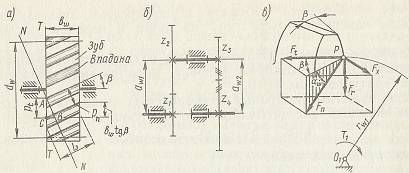
Рис. 8
Геометрические параметры.
В торцевой плоскости ТТ (Рис. 8,а) шаг зацепления
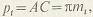
а в нормальном сечении NN шаг
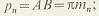
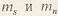 - торцовый и нормальный модули зацепления; стандартным является нормальный модуль. Из - торцовый и нормальный модули зацепления; стандартным является нормальный модуль. Из 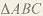 следует, что следует, что
поэтому 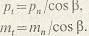
Делительный угол наклона линии зуба по начальному (делительному) цилиндру в большинстве передач принимается 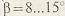 . Значения диаметров косозубого колеса (или шестерни), нарезанных без смещения, и другие размеры определяют по формулам, приведенным ранее для прямозубых колес: . Значения диаметров косозубого колеса (или шестерни), нарезанных без смещения, и другие размеры определяют по формулам, приведенным ранее для прямозубых колес:
делительный диаметр 
диаметр вершин зубьев 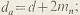
диаметр впадин: для 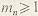 имеем имеем 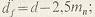 для для 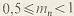 имеем имеем  . .
Межосевое расстояние косозубой цилиндрической передачи при 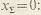 : :
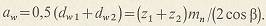
Силы, действующие в зацеплении. (Рис. 8,в). Нагрузка Fn, воспринимаемая зубом, направлена по нормали к его рабочей поверхности и может быть разложена на составляющие:
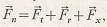
где Ft – окружная сила в торцовом сечении, линия действия которой касательна к начальной окружности, 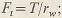 Fr – радиальная (распорная) сила, направленная по радиусу к центру колеса, Fr – радиальная (распорная) сила, направленная по радиусу к центру колеса, 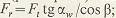 Fx – осевая сила, параллельная оси зубчатого колеса, Fx – осевая сила, параллельная оси зубчатого колеса, 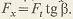 Эти силы вызывают сложную деформацию зубьев и нагружают валы и подшипники передачи. Эти силы вызывают сложную деформацию зубьев и нагружают валы и подшипники передачи.
Конические передачи.
Конические передачи применяют для преобразования вращательного движения между валами, оси которых пересекаются под некоторым углом Σ (Рис. 9 и 10) Конические колеса могут иметь прямые, косые и криволинейные зубья. Конические колеса изготавливают из такого же материала, что и цилиндрические, однако технология нарезания зубьев более сложная. Кроме того, валы и подшипники конических передач нагружаются как радиальными, так и осевыми, что несколько усложняет конструкцию этих узлов. Стоимость конических передач выше по сравнению с цилиндрическими, поэтому применение их должно иметь технико-экономическое обоснование.
В коническом колесе вместо торцевого сечения рассматривают сечение поверхностью дополнительного конуса, ось которого совпадает с осью колеса, а образующие перпендикулярны к образующим делительного конуса. Окружность, получаемую в результате пересечения делительного конуса и наружного дополнительного конуса, называют делительной окружностью конического колеса.
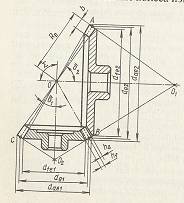
Рис. 9
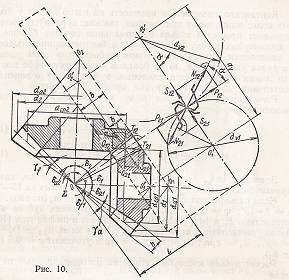
Силы, действующие на зубья.
Нормальную силу N12 , приложенную в средней точке полоски контакта зубьев, разложим на составляющие: окружную Р12 и радиальную для эквивалентного колеса S12 , действующую вдоль образующих средних дополнительных конусов, разложим на радиальную Q12 и осевую Т12 для конического колеса 2. Все силы выразим через окружную силу Р12, которую легко найти по заданному крутящему моменту М2 на ведомом валу (Рис. 10):
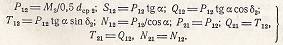
Действия этих сил учитывают при расчете зубьев колес, валов и подшипников механизма.
Момент на эквивалентном колесе
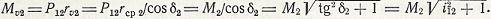
Геометрический расчет.
Конусы АОВ и ВОС сопряженных колес. (Рис. 9), которые при вращении катятся один по другому без скольжения, называются начальными (делительными) конусами. Их вершины находятся в точке пересечения геометрических осей колес. Окружности диаметров, полученные при пересечении делительных конусов и конусов АО1В и ВО2С, представляют собой делительные окружности. По этим окружностям определяют модуль зацепления конических колес, который стандартизован. Геометрический расчет ортогональной конической передачи ведется на основе следующих зависимостей:
внешний делительный диаметр 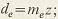
углы делительных конусов 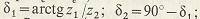
внешнее конусное расстояние 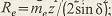
коэффициент ширины зубчатого венца 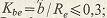
ширина венца зубчатого колеса 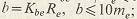
диаметры окружностей вершин и впадин
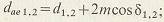
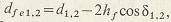
где внешняя высота 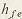 ножки зуба равна: ножки зуба равна: 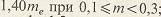 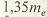 при при 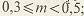 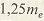 при при 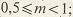 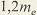 при при 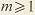 [средний окружной модуль [средний окружной модуль 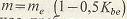 ] . ] .
Типовые конструкции конических колес (Рис. 11).
Конические колеса малых размеров d < 70 мм изготавливают со сплошным диском (Рис. 11,а). При d > 70 мм в целях снижения массы и момента инерции в диске колеса предусматривают отверстия и выточки (Рис. 11, б,в). Количество и размеры отверстий определяют также, как и для цилиндрических колес. Обычно ступица колеса располагается с противоположной стороны делительного конуса (Рис. 11,б), но может быть и так, как показано на рис. 11, в.
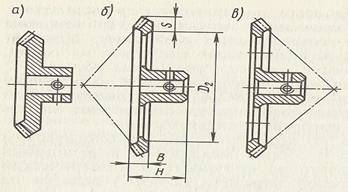
Рис. 11
Различают два способа образования зубьев: копирование и огибание. В приборостроении по способу копирования изготовляют зубчатые колеса штамповкой. Недостаток этого способа – относительно низкая точность получаемых параметров зацепления. Способ огибания (обкатывания) основной как в общем машиностроении, так и в приборостроении. Достоинства метода: высокая точность, большая производительность и возможность автоматизации процесса. Большую часть зубчатых колес в настоящее время изготовляют нарезанием. Одной из перспективных разновидностей нарезания колес методом огибания является накатка зубьев, которую применяют в основном при изготовлении мелкомодульных колес.
Габариты зубчатой передачи определяются ее межосевым расстоянием, которое зависит от модуля зацепления, передаточного отношения и числа зубьев шестерни.
Планетарные и дифференциальные механизмы.
Зубчатые передачи, имеющие колеса — сателлиты—, обкатывающиеся вокруг центральных колес и, следовательно, имеющие подвижные оси, называются эпициклическими. Эти передачи делятся на планетарные, имеющие одно ведущее звено, и дифференциальные, имеющие два ведущих звена.
Планетарные механизмы.
В зависимости от схемы планетарные механизмы могут осуществлять передаточные отношения от 3 до 1000 при к.п.д. от 0,98 до 0,01 соответственно. Ведущий и рабочий (выходной) валы расположены соосно. Размеры и массы— меньше, чем у зубчатых редукторов с неподвижными осями валов.
На рис. 12 приведены схемы наиболее распространенных планетарных механизмов с цилиндрическими зубчатыми колесами с внешним и внутренним зацеплением.
Планетарный механизм состоит из неподвижного центрального колеса z3, жестко связанного с корпусом, подвижного центрального колеса z1, сателлита с колесами z2 и z2' и водила Н, на котором закреплена подвижная ось сателлита. Сателлит вращается относительно своей оси и одновременно обкатывается вокруг колеса z1. Зубья колеса z1 нажимают на зубья колеса z2 сателлита и поворачивают его относительно неподвижного центрального колеса z3, при этом сателлит нажимает на ось водила и заставляет, водило Н вращаться. Ведущий валик колеса z1 и ведомый валик водила Н расположены соосно.
Планетарные механизмы обычно имеют размеры и вес меньшие, чем соответствующие им по силовым и кинематическим параметрам передачи с неподвижными осями колес. Это объясняется тем, что, применяя два или три сателлита, можно соответственно уменьшить нагрузку на зубья колес и использовать колеса с меньшими модулями и диаметрами.
Передаточное отношение планетарного механизма определяем методом обращения движения (остановки водила). Условно всем звеньям механизма сообщаем дополнительное движение с угловой скоростью водила wH, но в сторону, противоположную вращению последнего. Тогда угловые скорости: водила Н wH — wH = 0, колеса 1 w1 — wH, колеса 3 — wH, сателлита 2 w2 — wH и любого колеса k механизма wk — wH. Планетарный механизм превращается в механизм с неподвижными осями валов. Передаточное отношение преобразованного механизма от колеса 1 к колесу 3 при неподвижном водиле Н
.files/image002.jpg) (1) (1)
.files/image004.jpg)
Рис. 12.
Верхний индекс при i в круглых скобках обозначает неподвижное звено механизма. В нижнем индексе первая цифра обозначает валик ведущего, а вторая — валик ведомого (выходного) звена.
Из уравнения (1) находим формулу для определения передаточного отношения планетарного механизма от колеса 1 к водилу Н при неподвижном опорном колесе 3
.files/image006.jpg) (2) (2)
Передаточное отношение от водила H к колесу 1 находим, как обратное передаточное отношение
.files/image008.jpg) (3) (3)
Выбор схемы планетарного механизма производится с учетом рациональных значений передаточного отношения и к. п. д.
Основными параметрами планетарных механизмов являются: передаточное отношение от входного (ведущего) валика к выходному; к.п.д. механизма с подшипниками качения η; модуль m; числа зубьев колес .files/image010.jpg) диаметры колес диаметры колес .files/image012.jpg) число сателлитов K; условие соосности валиков; условие сборки число сателлитов K; условие соосности валиков; условие сборки .files/image014.jpg) , обеспечивающее равенство центральных углов γ между сателлитами ( , обеспечивающее равенство центральных углов γ между сателлитами ( .files/image014.jpg) — целое число); условие соседства при К > 3, обеспечивающее расположение нескольких сателлитов по окружности без соприкосновения их между собой ( — целое число); условие соседства при К > 3, обеспечивающее расположение нескольких сателлитов по окружности без соприкосновения их между собой ( .files/image016.jpg) рис. 12, схема I). рис. 12, схема I).
Схема I. Рациональные передаточные отношения .files/image018.jpg) к.п.д. η = 0,98…0,96. Так как к.п.д. η = 0,98…0,96. Так как .files/image020.jpg) , то передаточное отношение механизма , то передаточное отношение механизма
.files/image022.jpg) (4) (4)
Условие соосности: .files/image024.jpg)
Условие сборки: .files/image026.jpg)
Схема II. Эта схема редуктора составлена из двух последовательно соединенных схем I. Рациональные передаточные отношения .files/image028.jpg) ; к.п.д. η = 0,96…0,93. Передаточное отношение редуктора вычисляется по формуле ; к.п.д. η = 0,96…0,93. Передаточное отношение редуктора вычисляется по формуле
.files/image030.jpg) (5) (5)
Условие соосности: .files/image032.jpg) . .
Условие сборки: .files/image034.jpg) . .
Схема III. Рациональные передаточные отношения .files/image036.jpg) к.п.д. η = 0,98…0,96. Так как к.п.д. η = 0,98…0,96. Так как .files/image038.jpg) то передаточное отношение механизма то передаточное отношение механизма
.files/image040.jpg) (6) (6)
Условие соосности: m1 (z1 + z2) = m3 (z3 — z'2).
Условие сборки: (z3z2 + z1z'2)/ Kz2 =Θ.
Схема IV. Рациональные передаточные отношения IH1 = 30…1000 и более; к.п.д. η= 0,9…0,1. Передаточное отношение механизма определяется по формуле
.files/image042.jpg) (7) (7)
Условие соосности: .files/image044.jpg)
Условие сборки: .files/image046.jpg)
Приближенные значения к. п. д. при .files/image048.jpg)
.files/image050.jpg)
Схема V. Рациональные передаточные отношения .files/image052.jpg) и больше; и больше; .files/image054.jpg) . Передаточное отношение механизма вычисляется по формуле . Передаточное отношение механизма вычисляется по формуле
.files/image056.jpg) (8) (8)
Условие соосности: .files/image058.jpg)
Условие сборки: .files/image060.jpg)
.files/image062.jpg)
Рис. 13.
Числа зубьев колес подбирают путем совместного решения уравнений передаточного отношения и условия соосности с учетом условия сборки.
При больших передаточных отношениях для получения более высоких к. п. д. целесообразно применять схемы редукторов, составленные из нескольких последовательно соединенных схем I (рис. 12).
Силовой расчет. При заданных МH или М1, п1 (об/мин), i и η статические моменты М и мощности N на ведущих валах механизма определяем с учетом следующих зависимостей.
Для схем I, II и III (ведущее звено — валик с колесом 1):
.files/image064.jpg)
Для схем IV и V (ведущее звено — валик с водилом H):
.files/image066.jpg)
Силы, действующие на звенья механизма, можно определить, рассматривая условия равновесия каждого звена (рис. 13).
Определим приближенно (без учета к. п. д.) силы, действующие на звенья механизма, из схемы 1:
.files/image068.jpg)
Эти силы учитывают при расчете колес, валов и подшипников механизма.
Дифференциальные механизмы.
Эти механизмы имеют две степени свободы и отличаются от планетарных тем, что у них вращается не одно, а оба центральных колеса z1 и z3. Они применяются в вычислительных устройствах, следящих системах автоматического управления, приборах и машинах, когда требуется осуществить кинематическую связь между тремя валами.
Передаточное отношение дифференциального механизма определяют рассмотренным выше методом обращения движения
.files/image070.jpg) (9) (9)
Здесь и — число внешних зубчатых зацеплений.
Пользуясь этой зависимостью при заданных числах оборотов в минуту п любых двух ведущих валов, можно определить число оборотов третьего ведомого вала. При п3 = 0 или п1 = 0 дифференциальный механизм превращается в планетарный.
Наиболее часто применяются механизмы с коническими колесами — конические дифференциалы, у которых z1 = z3. На рис. 14 показаны схема и конструкция такого дифференциального суммирующего механизма, состоящего из водила Н, двух центральных колес z1 и z3, двух сателлитов z2 и стойки. Углы поворота центральных колес .files/image072.jpg) и и .files/image074.jpg) и водила φH связаны зависимостью и водила φH связаны зависимостью
.files/image076.jpg) (10) (10)
При заданных .files/image078.jpg) и и .files/image072.jpg) или или .files/image078.jpg) и и .files/image074.jpg) получим получим .files/image080.jpg) или или .files/image082.jpg) . .
.files/image084.jpg)
Рис. 14.
Кинематика планетарных и дифференциальных механизмов.
Основная задача кинематического анализа планетарных и дифференциальных передач — определение угловых скоростей ведомых звеньев. Для этого нужно иметь уравнение для передаточного отношения.
Рассмотрим планетарную передачу (см. рис. 18, а). Применим метод обращения движения (метод Виллиса), сообщив всей системе, вращение с угловой скоростью минус .files/image086.jpg) ( ( .files/image086.jpg) — угловая скорость водила h). Тогда водило оказывается неподвижным, а передача превращается в соосный зубчатый механизм с неподвижными осями — обращенный механизм (рис. 15). Угловые скорости звеньев исходного и обращенного механизмов: — угловая скорость водила h). Тогда водило оказывается неподвижным, а передача превращается в соосный зубчатый механизм с неподвижными осями — обращенный механизм (рис. 15). Угловые скорости звеньев исходного и обращенного механизмов:
.files/image088.jpg)
.files/image090.jpg)
Передаточное отношение обращенного механизма от звена 1 к звену 3
.files/image092.jpg)
Следовательно, искомое передаточное отношение от центрального колеса 1 к водилу h
.files/image094.jpg)
Передаточное отношение в обратном направлении
.files/image096.jpg)
При расчете передаточного отношения .files/image098.jpg) обращенного механизма с неподвижными в пространстве осями нужно учитывать знак передаточного отношения. Так как в рассматриваемой передаче оба зацепления внутренние, то в соответствии с формулами обращенного механизма с неподвижными в пространстве осями нужно учитывать знак передаточного отношения. Так как в рассматриваемой передаче оба зацепления внутренние, то в соответствии с формулами
.files/image100.jpg)
Следовательно, передаточное отношение планетарной передачи на рис. 19, а
.files/image102.jpg) (11) (11)
где Zj—число зубьев звена с номером .files/image104.jpg)
.files/image106.jpg)
Рис.16
В общем случае передаточное отношение между каким-либо центральным колесом к планетарной передачи и водилом h при неподвижном центральном колесе п определяется выражением .files/image108.jpg) ( ( .files/image110.jpg) —передаточное отношение между центральными колесами к и п при остановленном водиле h, т. е. передаточное отношение обращенного механизма). Например, для передачи на рис. 18,б опять получим выражение (11); для передачи на рис. 17, в передаточное отношение —передаточное отношение между центральными колесами к и п при остановленном водиле h, т. е. передаточное отношение обращенного механизма). Например, для передачи на рис. 18,б опять получим выражение (11); для передачи на рис. 17, в передаточное отношение
.files/image112.jpg)
а для передачи на рис. 17,б
.files/image114.jpg)
.files/image116.jpg)
Рис.17.
.files/image118.jpg)
Рис.18.
.files/image120.jpg)
Рис.19.
Угловую скорость ведомого звена дифференциального механизма проще всего рассчитать также с помощью метода обращения движения. Так как в дифференциальном механизме оба центральных колеса подвижны, то, сообщив всей системе вращение с угловой скоростью — .files/image086.jpg) , получим следующее выражение для передаточного отношения обращенного механизма (с неподвижным водилом): , получим следующее выражение для передаточного отношения обращенного механизма (с неподвижным водилом):
.files/image122.jpg)
где .files/image086.jpg) , , .files/image124.jpg) , , .files/image126.jpg) — абсолютные угловые скорости соответствующих звеньев дифференциального механизма. Передаточное отношение — абсолютные угловые скорости соответствующих звеньев дифференциального механизма. Передаточное отношение .files/image128.jpg) выражается через числа зубьев колес, две угловые скорости определены законом движения двух входных звеньев; поэтому в уравнении одно неизвестное — угловая скорость выходного звена. Например, если центральные колеса 1 и 3— входные звенья, то угловую скорость выходного водила h вычисляют из уравнения выражается через числа зубьев колес, две угловые скорости определены законом движения двух входных звеньев; поэтому в уравнении одно неизвестное — угловая скорость выходного звена. Например, если центральные колеса 1 и 3— входные звенья, то угловую скорость выходного водила h вычисляют из уравнения
.files/image130.jpg)
Для дифференциального механизма на рис. 17,а это выражение с учетом числа зубьев принимает вид
.files/image132.jpg)
Аналогично получают зависимости для расчета передаточного отношения замкнутой дифференциальной передачи. В отличие от предыдущего здесь угловые скорости .files/image124.jpg) и и .files/image126.jpg) жестко связаны друг с другом. Так, для механизма на рис. 20 эта связь имеет следующий вид: жестко связаны друг с другом. Так, для механизма на рис. 20 эта связь имеет следующий вид:
.files/image134.jpg)
.files/image136.jpg)
Рис.20
С учетом выражений угловую скорость выходного водила и передаточное отношение рассматриваемого замкнутого дифференциального механизма вычисляют по формулам:
.files/image138.jpg)
При выборе числа зубьев колес для обеспечения необходимого передаточного отношения механизма нужно соблюсти следующие условия: соосности, сборки и соседства, отсутствия интерференции и самоторможения.
Условие соосности предусматривает совпадение геометрических осей центральных колес; для передачи на рис. 17,б условие соосности
.files/image140.jpg)
откуда для передачи, состоящей из колес, нарезанных без смещения,
.files/image142.jpg)
для передачи на рис. 18,б
.files/image144.jpg)
или
.files/image146.jpg)
где .files/image148.jpg) — начальные радиусы; m12, m2'3 — модули зацепления соответствующих пар колес, для косозубых колес эти модули — торцовые. — начальные радиусы; m12, m2'3 — модули зацепления соответствующих пар колес, для косозубых колес эти модули — торцовые.
Условия соосности для схем на рис. 18,а, в;
.files/image150.jpg)
При несоблюдении условия соосности можно, не изменяя значений модулей и чисел зубьев, выбрать нужный для соосности угол β наклона зубьев или коэффициент суммы смещений x∑.
Условие сборки дает возможность равномерно распределить несколько сателлитов по окружности центральных колес. Необходимость этого обусловлена тем, что установка в механизм первого сателлита определяет такое взаимное расположение центральных зубчатых колес и водила, при котором установка остальных сателлитов может оказаться невозможной. В передаче, изображенной на рис. 17, в, угол между осями сателлитных колес .files/image152.jpg) (q — число сателлитов); при повороте водила на этот угол центральное колесо повернется на угол (q — число сателлитов); при повороте водила на этот угол центральное колесо повернется на угол
.files/image154.jpg)
а сателлитные колеса должны поменяться местами (относительно центрального колеса 1). Это возможно при условии, что длина дуги .files/image156.jpg) без остатка делится на шаг pw, т. е. отношение без остатка делится на шаг pw, т. е. отношение .files/image158.jpg) должно быть целым числом. Для передач по схеме рис. 17,б и 18, а, б, в условие сборки (после преобразований) получит соответственно следующий вид: должно быть целым числом. Для передач по схеме рис. 17,б и 18, а, б, в условие сборки (после преобразований) получит соответственно следующий вид:
.files/image160.jpg)
здесь верхний знак берется при расчетах механизмов с разноименными зацеплениями, а нижний — с одноименными.
Условие соседства устанавливает наибольшее возможное число сателлитных колес при отсутствии касания (задевания) вершин их зубьев. Касание отсутствует при соблюдении неравенства .files/image162.jpg) (см. рис. 17, в); так как (см. рис. 17, в); так как .files/image164.jpg) то условие соседства то условие соседства
.files/image166.jpg)
Для нулевых колес с коэффициентом высоты головки зуба ha* = 1, а также для равносмещенной передачи .files/image168.jpg) неравенство принимает следующий вид: неравенство принимает следующий вид:
.files/image170.jpg)
где qmax— наибольшее возможное количество сателлитных колес.
В механизмах, выполненных по схемам на рис. 18, условие должно выполняться для каждого из зацеплений 1-2 и 2'-3. Выполнение условия соседства проверяют при q>2 для механизмов по схеме на рис. 17 и внешних зацеплений (см. рис. 18), при q ≥ 2 — для внутренних зацеплений.
Дополнительные условия. Кроме рассмотренных специфических условий нужно соблюдать все ограничения, налагаемые на числа зубьев передач с неподвижными осями. Для внешнего зацепления такое ограничение — возможное подрезание зубьев, а для внутреннего — их интерференция, т. е. пересечение профилей и заклинивание зубьев. Чтобы в зацеплении колеса 2 (2') (см. рис. 18, a, в), имеющего внешние зубья, с колесом 1 (3), имеющим внутренние зубья, не было заклинивания, необходимо при подборе числа зубьев выполнить неравенство:
.files/image172.jpg)
при угле профиля рейки a = 20° и h*a=1
.files/image174.jpg)
Для предотвращения интерференции при нарезании внутренних зубьев без сдвига инструмента разность чисел зубьев должна быть не менее .files/image176.jpg) . Эти ограничения часто приводят к увеличению габаритов передачи. Применение цевочного зацепления и зацепления Новикова позволяет применить колеса внутреннего зацепления с меньшим числом зубьев. Поэтому цевочное зацепление часто применяют в приборных планетарных передачах. . Эти ограничения часто приводят к увеличению габаритов передачи. Применение цевочного зацепления и зацепления Новикова позволяет применить колеса внутреннего зацепления с меньшим числом зубьев. Поэтому цевочное зацепление часто применяют в приборных планетарных передачах.
Условие отсутствия самоторможения η > 0 нужно выполнить для того направления передачи энергии, при котором данная передача используется.
Выбор чисел зубьев колес планетарной передачи, которые бы удовлетворяли всем приведенным выше условиям, является сложной задачей. Для удобства ее решения можно соединить уравнения, выражающие передаточное отношение и условия соосности и сборки, в одно общее уравнение. Такое общее уравнение для выбора чисел зубьев планетарной передачи по схеме на рис. 17,б может быть представлено в следующем виде:
.files/image178.jpg)
Здесь z1—число зубьев центрального колеса, которое должно быть для нулевых колес не меньше 17 и кратным полученным значениям A, В, С. Выбрав с учетом этого число зубьев z1, из уравнения находят числа зубьев остальных колес и проверяют их по условию соседства.
Для планетарной передачи по схеме на рис. 18,б при одном блоке сателлитов выбор чисел зубьев колес может быть проведен с учетом двух условий: обеспечения заданного передаточного отношения и соосности передачи. Первое условие выражается зависимостью , из которой следует:
.files/image180.jpg)
Ориентировочно можно принять для схемы на рис. 18,б:
.files/image182.jpg)
Выбрав число зубьев центрального колеса z1 и отношение чисел зубьев сателлитов z2'/z2, определяют по формуле значение z3, которое должно быть целым числом.
Соблюдение этого условия может быть обеспечено выбором соответствующего модуля зацепления второй ступени передачи:
Для удобства согласования значения модуля со стандартным вторую ступень часто выполняют косозубой с углом наклона зубьев β2'3. В этом случае нормальный модуль зацепления, подлежащий согласованию со стандартом
.files/image186.jpg)
Червячные передачи.
Червячные передачи применяют для преобразования вращательного движения между двумя скрещивающимися валами. Они позволяют получить в одной ступени большие передаточные числа (до 500), обладают плавным и бесшумным ходом, могут обеспечить самоторможение. Передача синтезирована из двух механизмов — винт-гайка и косозубое цилиндрическое зацепление; червяк — это винт с числом заходов от одного до пяти, червячное колесо — косозубое цилиндрическое, конструкция венца которого имеет некоторые особенности. В приборах применяются упрощенные червячные передачи.
Виды и применение.
На рис. 21, а представлена конструкция червячной передачи. Входным звеном чаще всего является червяк I, который представляет собой винт; выходное звено — червячное колесо 2. Преобразование движения в обратном направлении возможно в несамотор-мозящих передачах, которые применяют, например, в регуляторах скорости. Кроме указанных выше достоинств червячные передачи обеспечивают малые габариты и массу приводного механизма, а также небольшой мертвый ход. К недостаткам червячных передач относятся сравнительно низкий кпд при больших передаточных числах, повышенный износ, относительно высокая стоимость изготовления и строгие требования к точности изготовления и сборки.
.files/image002.jpg)
Рис. 21
.files/image004.jpg)
Рис.22
.files/image006.jpg)
Рис.23
Червячные передачи применяют в системах автоматики и ЭВМ как самостоятельно, так и в сочетании с другими механизмами. Например, в приводе переключателя контактов радиозонда (рис. 22) трехступенчатый червячный механизм связывает вал I электродвигателя М с валом II, на котором жестко закреплен переключатель. При этом обеспечивается общее передаточное число 12 800.
Червячные передачи могут быть с цилиндрическим (см. рис. 21) и глобоидным (рис. 23) червяком. Последние обеспечивают повышенную нагрузочную способность, но в точной механике практически не используются. В зависимости от способа образования боковых поверхностей витков цилиндрические червяки подразделяют на архимедовы, конволютные и эвольвентные. Благодаря относительной простоте изготовления наибольшее распространение получили архимедовы червяки, у которых профиль витка червяка в осевом сечении — равнобедренная трапеция, т. е. профиль такой же, как и у рейки эвольвентного зацепления (рис. 24). Поэтому зуб червячного колеса в сечении Б—Б очерчивается эвольвентой. Конволютные червяки применяют вместо архимедовых при больших углах подъема линии витка. Виток этого червяка в торцовом сечении имеет профиль в виде эвольвенты. В тех случаях, когда требуется увеличить к.п.д. механизма, используют червяки с эвольвентиым профилем в осевом сечении.
Если червяк выполнен так, что точка, движущаяся вдоль линии витка на рис. 21, б, поднимается вверх и смещается слева направо, то такой червяк называют правым. В том случае, когда линия витка навита в противоположном направлении, червяк — левый. В червячных передачах, отличающихся лишь видом червяка (правый или левый), при одинаковом вращении ведущего звена ведомые звенья вращаются в разные стороны.
В зависимости от особенностей конструкции червячного колеса передачи подразделяются на следующие типы:
цилиндрический червяк 1 сопрягается с червячным колесом 2, зубья которого имеют вогнутую форму и охватывают червяк (рис. 16.5, а); угол скрещивания осей валов передачи 90°, ось червяка лежит в средней плоскости колеса; это наиболее распространенный вид червячных передач;
цилиндрический червяк сопрягается с прямозубым цилиндрическим колесом (рис. 25,6); угол скрещивания Е = 90° — у (у — длительный угол подъема средней линии витка червяка);
цилиндрический червяк сопрягается с косозубым колесом (рис. 25, б); угол скрещивания 90"; такой тип передачи применяют преимущественно в приборах с малыми нагрузками на зубья.
В первой из рассмотренных схем контакт зубьев линейный, что благоприятно в отношении нагрузочной способности и минимизации износа. В передачах (рис. 25, б, в) контакт зубьев точечный, что определяет небольшую нагрузочную способность и повышенный износ.
.files/image008.jpg)
Рис.24
Угол между осями валов червяка и червячного колеса чаще всего равен 90° (ортогональная передача). В приборостроении и ЭВМ находят применение также неортогональные передачи (рис. 25, б).
Преобразование движения в червячной передаче сопровождается скольжением витков червяка по зубьям колеса, что вызывает значительное трение и износ соприкасающихся поверхностей. Эта особенность предопределяет выбор материала для изготовления червяков и колес, обеспечивающих наименьшие трение и износ. Так как витки червяка нагружаются значительно чаще, чем зубья колеса, то для изготовления червяков применяют стали марок 20; 45; 15Х; 40ХМ; 40ХН; 12ХНЗА и др.; рабочие поверхности витков подвергают закалке до твердости 45...65 HRC. Червячные колеса изготовляют обычно из бронзы или синтетических материалов. Лучшими антифрикционными свойствами обладают бронзы БрОФЮ—1, БрОНФ—10—1 —1, из которых изготовляют червячные колеса (или венцы колес) ответственных передач при скорости скольжения, превышающей 3 м/с. Безоловянные бронзы типа БрАЖ9 — 4, БрАЖНЮ—4—4 менее дороги, но механические свойства их ниже первых, поэтому они применяются для менее ответственных передач. В механических системах автоматики и ЭВМ широко применяют червячные колеса из синтетических материалов: полиамидов, капрона, кап-ролона, текстолита и др. Колеса из этих материалов отличаются хорошими антифрикционными свойствами и достаточной износостойкостью.
.files/image010.jpg)
Рис.25
Основные параметры и конструкции.
При проектировании червячных передач размеры и параметры их элементов определяют на основании геометрического и прочностного расчетов.
Передаточное отношение назначают по заданным условиям на проектирование, учитывая, что посредством одноступенчатой червячной передачи можно реализовать передаточное число в пределах 6...300 и более. Передаточное число может быть как целым, так и дробным; выбор целых чисел способствует более быстрой приработке зубьев колеса и повышению износостойкости передачи.
Передаточное отношение. Чтобы вывести зависимость, связывающую передаточное отношение червячной передачи с ее параметрами, рассмотрим движение точки А (см. рис. 21,б). Так как червяк является винтом, то точка А, расположенная на его делительном цилиндре диаметром dx, за один оборот червяка переместилась бы в механизме винт-гайка вдоль образующей ММ вместе с гайкой на ход резьбы s = zlp (p — шаг резьбы, см. рис. 21,б, Zj—число заходов червяка). Червяк вращается с частотой , (об/мин). Поэтому за одну минуту путь точки А вдоль образующей делительного цилиндра
.files/image012.jpg)
За это время точка А, принадлежащая червячному колесу 2, переместится на расстояние
.files/image014.jpg)
где n2 — частота вращения колеса, об/мин; d2 = mz2—делительный диаметр колеса; z2 — число его зубьев. Передаточное отношение найдем, приравняв выражения и (с учетом соотношения между шагом р и модулем т=рpi).
Геометрический расчет червячной передачи.
Цель геометрического расчета червячных передач — определение или выбор размеров элементов червяка и колеса. Исходные данные — модуль зацепления т, число витков (заходов) червяка z1, т. е. число нитей резьбы, навитых на делительный цилиндр диаметром d1, передаточное отношение, а также коэффициент диаметра червяка
.files/image016.jpg)
Стандартным для червяка является осевой модуль т, который равен торцовому модулю червячного колеса. Значения параметров m и q назначаются в зависимости от конструкторско-технологических условий в соответствии с ГОСТ 19672—74 (СТ СЭВ 267—76):
.files/image018.jpg)
Меньшие значения q применяются в быстроходных передачах для ограничения окружных скоростей, большие — для повышения жесткости червяка при высоких передаточных отношениях.
Стандартный угол профиля червячного зацепления .files/image020.jpg) (см. рис. 24). (см. рис. 24).
Найдем связь между геометрическими параметрами червяка. С этой целью развернем на плоскость делительный цилиндр диаметром d1, разрезав его вдоль образующей ММ (см. рис. 21, б). При этом нить а резьбы отобразится в гипотенузу ВВ1 треугольника ВВВ1, горизонтальный катет которого — развертка окружности диаметра d1, острый угол γ—делительный угол подъема линии витка, т. е. угол, который составляет касательная к винтовой линии в точке В с горизонтальной плоскостью. На рис. 21, б показан двухзаходныи червяк (z1 = 2); при его развертке вторая винтовая линия δ отображается в прямую CC1. Из ∆ВВВ1 найдем, учитывая определение модуля .files/image022.jpg) , ,
.files/image024.jpg)
Полученная формула связывает угол γ, число витков червяка z1 и коэффициент диаметра червяка q.
В первом приближении параметры передачи выбирают с помощью графиков (рис. 26): слева от заштрихованной зоны расположена область самотормозящих механизмов, справа — несамотормозящих; в заштрихованной зоне в зависимости от примененных материалов и других условий могут существовать как самотормозящие, так и несамотормозящие передачи; кпд растет с увеличением угла γ.
.files/image026.jpg)
Рис. 26
Число витков червяка назначается в пределах z1 = 1…5, а число зубьев червячного колеса z2 определяется по формуле; рекомендуется принимать z2 не менее 28. Для больших значений передаточного числа (60 и более) в целях снижения размеров передачи принимают z1 = 1 или 2. Назначая z1, можно использовать следующие рекомендации:
.files/image028.jpg)
Точность передачи снижается с увеличением числа витков z1, так как возможная разность хода витков червяка порождает периодические ошибки в движении колеса. Учитывая это, в отсчетных передачах отдают предпочтение однозаходным червякам.
Геометрический расчет элементов червячной передачи (см. рис. 24) проводят по формулам, приведенным в табл. 1. Эти зависимости аналогичны тем, которые использованы для расчета цилиндрических колес; здесь коэффициент высоты головки зуба ha*=l, радиального зазора с* = 0,2 (ГОСТ 19036—81). Учтено также что в сечении Б—Б (см. рис. 16.4) червячное колесо такое же, как цилиндрическое косозубое с углом γ наклона зубьев; отличие между ними состоит только в том, что стандартный модуль червячного колеса (торцовый) равен осевому модулю т червяка (у косозубого цилиндрического колеса стандартный модуль —нормальный).
Таблица 1. Формулы для расчета червячной передачи.
.files/image030.jpg)
Кпд передачи. При определенном модуле и числе витков значение параметра q определяет жесткость червяка и кпд передачи: чем больше значение q, тем большей жесткостью обладает червяк. Кпд при ведущем червяке определяют по формуле
.files/image032.jpg)
где .files/image034.jpg) — приведенный угол трения, соответствующий приведенному коэффициенту f' трения скольжения (зависит от материала, шероховатости трущихся поверхностей, смазки и ряда других факторов). При ориентировочных расчетах можно принимать — приведенный угол трения, соответствующий приведенному коэффициенту f' трения скольжения (зависит от материала, шероховатости трущихся поверхностей, смазки и ряда других факторов). При ориентировочных расчетах можно принимать .files/image036.jpg) .files/image038.jpg) и считать, что кпд η12 принимает следующие значения: и считать, что кпд η12 принимает следующие значения:
.files/image040.jpg) Хорошо выполненная передача может иметь кпд, значительно превышающий ориентировочные значения. Хорошо выполненная передача может иметь кпд, значительно превышающий ориентировочные значения.
При ведущем колесе
.files/image042.jpg)
Механизм будет самотормозящим, т. е. передача энергии от червячного колеса невозможна в том случае, когда выполняется неравенство .files/image044.jpg) . При ведущем червяке механизм работает, хотя значения кпд могут быть и небольшими. Найдем верхний предел кпд η12 при ведущем червяке для самотормозящей передачи. Из условия . При ведущем червяке механизм работает, хотя значения кпд могут быть и небольшими. Найдем верхний предел кпд η12 при ведущем червяке для самотормозящей передачи. Из условия .files/image044.jpg) следует неравенство следует неравенство .files/image046.jpg) , так как все рассматриваемые углы — острые. Тогда при замене в формуле , так как все рассматриваемые углы — острые. Тогда при замене в формуле .files/image048.jpg) на на .files/image050.jpg) знаменатель уменьшается, т. е. знаменатель уменьшается, т. е. .files/image052.jpg) Следовательно, кпд самотормозящей червячной передачи при ведущем червяке (когда возможно движение) не может превышать 0,5. Следовательно, кпд самотормозящей червячной передачи при ведущем червяке (когда возможно движение) не может превышать 0,5.
Силы в зацеплении распределены по линии контакта зуба колеса с витком червяка. Существенную роль играют силы трения, которые зависят от скорости скольжения в каждой точке контакта и от ряда других факторов (режимы работы, смазки, коэффициента перекрытия и др.). В первом приближении все распределенные нагрузки заменяют сосредоточенной силой, приложенной в полюсе зацепления (точка А на рис. 21). Сила Fnl действует на витки червяка 1, сила Fn2 — на зубья колеса 2. На рис. 27, а показаны проекции этих сил — окружные Ft, радиальные Fr и осевые Fx составляющие. Окружные силы касательны к делительным окружностям и вычисляются по формулам:
.files/image054.jpg)
где Т1—крутящий момент на червяке, Т2 — то же, на колесе; d1d2—делительные диаметры; для ведущего звена окружная сила направлена против скорости точки приложения, а для ведомого — по скорости. Так как колесо червячной передачи такое же, как в косозубой цилиндрической, угол наклона зубьев которой β = γ, то радиальную и осевую силы находим по формулам:
.files/image056.jpg)
.files/image058.jpg)
Рис.27
Потери на трение учитываются при расчете момента сил на ведущем звене по известному моменту на ведомом:
.files/image060.jpg)
Силы трения практически не влияют на положение линии действия силы Fn1, т.е. линия действия полной силы Fnl(Fxl, Ft1, —Frl) нормальна к рабочей поверхности витка червяка. Эта поверхность получена вращением прямой пп (правый профиль, см. рис. 27, б) или n1n1 (левый профиль) вокруг оси х с одновременным смещением вдоль этой оси на величину .files/image062.jpg) . Для правого профиля и правой навивки винтовой линии уравнения винтовой поверхности: . Для правого профиля и правой навивки винтовой линии уравнения винтовой поверхности:
.files/image064.jpg)
где угол φ поворота прямой пп и радиус р—независимые переменные; начало отсчета φ— от плоскости ху. Вектор нормали к поверхности
.files/image066.jpg)
где .files/image068.jpg) — орты осей х, у, z (вторая и третья строки содержат частные производные координат). Для точек контакта (рис. 27, а) угол — орты осей х, у, z (вторая и третья строки содержат частные производные координат). Для точек контакта (рис. 27, а) угол .files/image070.jpg) при правой навивке. Поэтому из определителя получим следующие координаты вектора нормали: при правой навивке. Поэтому из определителя получим следующие координаты вектора нормали:
.files/image072.jpg)
Напряжения силы Fn1 и вектора нормали n совпадают, поэтому проекции Fn1 можно записать в таком виде:
.files/image074.jpg)
где n — модуль вектора нормали. Выразив осевую Fxl и радиальную Frl составляющие через окружную силу Ft1=Fnny/n, получим расчетные формулы:
.files/image076.jpg)
Эти зависимости, выведенные для правого профиля витка и для правой навивки, верны и для всех других случаев.
|