Винтовые передачи

Винтовые механизмы. В винтовых механизмах используют винтовые кинематические пары V класса. Обычно они служат для преобразования вращательного движения в поступательное со значительным уменьшением скорости.

Основными деталями винтового механизма являются цилиндр с наружной резьбой (винт) и кольцо с внутренней резьбой (гайка).

При этом резьбой называется поверхность, получающаяся при перемещении некоторого профиля по винтовой линии. В зависимости от числа элементов профиля различают одно- или многозаходные резьбы. В соответствии с направлением винтовой линии резьба может быть правой или левой. Наибольшее распространение получили правые резьбы.

В зависимости от характера движения винта и гайки механизмы подразделяют на четыре группы:

с вращающейся гайкой и поступательно движущимся винтом (рис. 63, а);

с вращающимся винтом и поступательно движущейся гайкой (рис. 63, б);

с неподвижным винтом и гайкой, находящейся в винтовом движении (рис. 63, е);

с неподвижной гайкой и винтом, находящимся в винтовом движении (рис. 63, г).

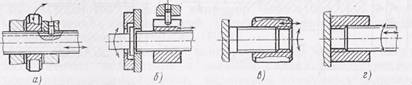
Рис. 63. Варианты работы винтовых механизмов.

Последний вариант обеспечивает наибольшую точность движения и широко используется в различных измерительных приборах (например, в микрометрах и т. п.).

По назначению винтовые механизмы делят на силовые и кинематические. Силовые механизмы предназначены для значительных нагрузок. Они должны иметь высокий КПД и достаточную прочность элементов передачи — резьбы. Кинематические механизмы применяют для точных перемещений узлов приборов и регулирования взаимного расположения деталей. Кинематические механизмы должны иметь достаточную точность преобразования движения, в них должны отсутствовать мертвые ходы за счет зазоров в резьбах, т. е. должны быть минимальными накопленная и циклическая погрешности.

В винтовых механизмах применяют резьбы различных видов.

Резьбу метрическую применяют для крепежных деталей и кинематических винтовых механизмов; она, как правило, имеет один заход (рис. 64). Основные параметры метрической резьбы: d — номинальный диаметр резьбы, равный наружному диаметру болта и гайки (d = D); P — шаг резьбы; у — угол профиля резьбы, равный 60°. Номинальный диаметр резьбы и ее шаг выбирают в соответствии со стандартами ГОСТ 9150—81, ГОСТ 8724—81, ГОСТ 24705—81, ГОСТ 24706—81.

Остальные геометрические параметры резьбы определяются через известные (рис. 64) по формулам: теоретическая высота профиля ;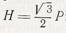

средний диаметр болта (гайки) d2(D2) = d - ¾*H; внутренний диаметр болта (гайки) d1(D1) = d - 5/4*H; рабочая высота профиля H1=5/8*H.

Резьба с одним наружным диаметром может иметь различные шаги. Например, резьба с d = 10 мм может иметь Р = 0,5; 0,75; 1; 1,25 и 1,5 мм. Резьбу с максимальным или крупным шагом обозначают буквой М и номинальным диаметром, например: М10, М12 и т. д. Многозаходные резьбы обозначают

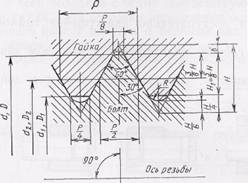
Рис. 64. Профиль метрической резьбы для диаметров 0,25—600 мм

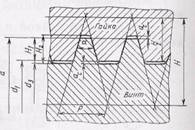
Рис. 65. Профиль трапецеидальной резьбы для диаметров 10—640 мм

буквой М, номинальным диаметром, числовым значением хода и в скобках буквой Р и числовым значением шага. Например, трехзаходная резьба с шагом 1 мм имеет ход, равный 3 мм; следовательно, ее обозначение при номинальном диаметре 24 мм: М24ХЗ (Р1). Если используется левая резьба, то после условного обозначения добавляют буквы LH, например: M24LH.

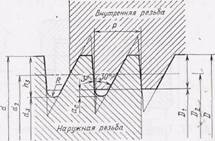
Рис. 66. Профиль упорной резьбы.

Резьбу трапецеидальную применяют исключительно для винтовых механизмов, чаще в силовых конструкциях, если осевая сила может действовать в любом направлении (рис. 65). В трапецеидальной резьбе, как и в метрической, стандартом определены d —D, Р и угол профиля v, равный 30° (ГОСТ 9484—81, ГОСТ 24737—81, ГОСТ 24738—81, ГОСТ 24739—81).

Остальные параметры резьбы определяют по формулам: теоретическая высота H = 1,866*Р; H1 = 0,5*Р; глубина резьбы H2 = 0,5*Р + а0.; зазор а0 = 0,25 мм для резьб с Р = 2 - 5 мм, а0 = 0,5 мм для резьб с Р = 6 - 12 мм и а0 = 1 для резьб с Р = 16 мм и более; средний диаметр d2 = d - 0,5*Р; внутренний диаметр резьбы винта d3 = d - 2*H2; внутренний диаметр резьбы гайки d1 = d1 = d - Р; наружный диаметр резьбы гайки D4 = d + 2а0.

Винтовые механизмы с трапецеидальными резьбами имеют более высокий КПД, чем с метрическими, но ограничены минимальным размером d = 8 мм. Кроме того, трапецеидальная резьба обеспечивает большую точность осевого перемещения ведомого звена, поскольку ввиду меньшего угла профиля одинаковые погрешности толщины витков и зазоры вызывают меньшие первичные погрешности. Метрическая резьба имеет меньшие погрешности (в радиальном направлении) винта или гайки.

Условия изготовления делают целесообразным применение в точных механизмах с мелкими шагами (<1 мм) только метрической резьбы, а с большими — трапецеидальной.

Число параллельных ниток резьбы или заходов для многозаходных трапецеидальных резьб выбирают равным 2, 3, 4, 6 или 8.

Трапецеидальную однозаходную резьбу обозначают размером наружного диаметра и шага, например TrбЗх10.

В обозначение многозаходной резьбы дополнительно вводят ход резьбы, например Tr80x40 (P10).

Резьбу упорную (рис. 66) используют для тяжело нагруженных винтовых механизмов с осевыми силами, действующими в одном направлении (прессы, механизмы вакуумных задвижек и др.).

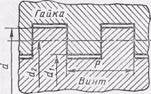
Рис. 67. Профиль прямоугольной резбы.

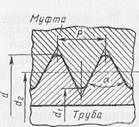
Рис. 68. Профиль трубной цилиндрической резьбы.

Профиль резьбы несимметричен по отношению к торцовому сечению (углы профиля 30 и 3°). Основные геометрические параметры резьбы определяют из соотношений (ГОСТ 10177—82)

d2 = D2 =d – 0,75*P; d3 = d – 1,735534*P;

D1 = d – 1,5*P; H = 1,587911*P; H1=0.75*P;

a0 = 0,117767*P; R = 0,124271*P.

При этом исходными для расчета являются стандартные параметры: шаг, выбираемый в пределах Р = 2 - 48 мм, и наружный диаметр резьбы d = 10 - 640 мм. Резьбу обозначают буквой S, номинальным диаметром и шагом, например 880x10. Многозаходную резьбу обозначают буквой S, номинальным диаметром, числовым значением хода, в скобках буквой Р и числовым значением шага; например, для двухзаходной резьбы с шагом 10 мм — 880x20 (Р10).

Резьбу прямоугольную (рис. 67) применяют с большим числом заходов (более трех) в оптико-механических и других специальных приборах. Она нестандартна и не обеспечивает взаимного центрирования деталей, технологически более трудоемка и менее прочна.

Специальные резьбы служат для соединения труб и арматуры трубопроводов. К этой группе крепежных резьб относятся трубные цилиндрические резьбы (рис. 68). Их обозначают по внутреннему размеру трубы, выраженному в дюймах, например G1/2 (ГОСТ 6357—81). Профиль резьбы представляет собой равнобедренный треугольник с углом при вершине 55°.

К специальным резьбам относятся также круглые резьбы (СТ СЭВ 307—76) (рис. 69), применяемые в цоколях электроламп и некоторых других случаях.

Силовые зависимости в винтовых механизмах. При использовании резьб в силовых винтовых механизмах основной задачей является определение момента М, действующего на вращающуюся деталь (винт или гайку) для преодоления определенной осевой нагрузки Q.

Рассмотрим равномерное вращение винта, нагруженного осевой силой Q, относительно неподвижной гайки.

Развернув один виток резьбы, получим клиновой механизм с углом клина, равным углу подъема резьбы (рис. 70). Ход резьбы,

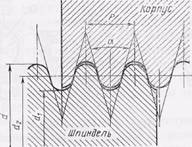
Рис. 69. Профиль круглой резьбы.

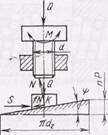
Рис. 70. Силы, действующие в винтовом механизме.

или осевое перемещение винта за один полный оборот Ph = n*P, где п — число заходов или параллельных ниток резьбы. Угол подъема резьбы

На резьбу действует сила N нормального давления, или нормальная реакция. f'*N — сила трения (f' = arctg r, где r — угол трения). Спроектируем все силы на координатные оси:

Исключив из уравнений силу N, определим окружное усилие S, необходимое для движения ползуна клинового механизма, S = Q*tg(y + r).

Распространим полученное уравнение на элементы резьбы. Учитывая, что сила S направлена по касательной к окружности среднего диаметра d2, получим

 

Используя эту зависимость, определим КПД винтового механизма, сравнивая полезную и затраченную работу при одном полном обороте винта:

h=Aп/Aз=tgy/tg(y + r).

Из выражения (56) видно, что КПД механизма, прежде всего, определяется углом подъема винтовой линии и, следовательно, числом заходов. При увеличении числа заходов КПД повышается.

Самоторможение винтовых механизмов. В отличие от многих других механизмов (рычажных, зубчатых и др.) в винтовых механизмах ведущее звено, как правило, имеет вращательное движение, а ведомое — поступательное. При определенных условиях возможна передача движения и в обратном направлении. Такие механизмы называются несамотормозящимися.

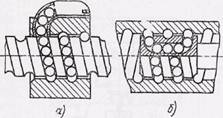
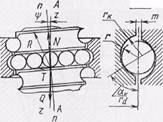
Рис. 71. Шариковинтовой механизм:

а — в гайке; б — в винте.

Рис. 72. Схема передачи усилий в шариковинтовом механизме.

Действующая осевая сила Q может вызывать поворот винта относительно гайки. Самоторможение отсутствует, если достаточно велик угол подъема винтовой линии. В этом случае момент от возникающих в резьбе сил трения f*N меньше, чем раскручивающий момент, возникающий от осевой силы Q (см. рис. 70).

Определим значение минимального угла y, при котором самоторможение отсутствует. Спроектируем все силы на оси n и τ:

Решив систему уравнений, получим

Таким образом, винтовой механизм будет самотормозящимся, если y < r, и несамотормозящимся при y > r.

При определении угла трения следует учитывать, что сила реакции N составляет с направлением оси винта угол γ/2 (где γ — угол профиля резьбы). В результате f' = f/cos(γ/2), где f — коэффициент трения между материалами винта и гайки.

Для снижения угла трения (повышения КПД) трение скольжения в винтовой паре заменяют трением качения. Винтовые пары с трением качения образуются шариками, расположенными между винтовыми дорожками винта и гайки. Для обеспечения вращения в одном направлении шарики должны возвращаться в исходное положение. С этой целью в конструкции шариковинтового механизма (рис. 71) предусматривается рециркуляционное устройство (сбводной канал). Число шариков, циркулирующих в замкнутой системе, обычно не превышает 50. При большем числе шариков возрастают потери на трение в сбводном канале, и КПД уменьшается.

Для определения КПД используют формулу (56), в которой угол трения

где k - коэффициент трения качения (k = 0,03 - 0,08 мм); dш - диаметр шарика (dш = 2*г); αк — угол контакта (рис. 72).

Шариковинтовые механизмы нашли широкое применение в устройствах, работающих без смазки и обеспечивающих малый коэффициент трения покоя, высокий КПД (до 0,98), незначительный износ, стабильную точность перемещения, возможность движения под действием силы тяжести (несамотормбзящиеся механизмы), что особенно важно для работы механизмов управления в режиме аварийной защиты.

Прочностной расчет элементов винтовых механизмов. Такой расчет проводят для предотвращения поломки винта, изнашивания резьбы, а при значительных длинах винта — для предотвращения потери устойчивости. В поперечном сечении винта действует нормальное напряжение растяжения (или сжатия), возникающее от осевой силы Q:

и касательное напряжение от вращающего момента М

где W' — момент сопротивления площади сечения.

Эквивалентное (приведенное) напряжение

Считая, что d1 ≈ d2, а для одно- и двухзаходных резьб коэффициент трения f ≈ 0,15 - 0,2, получим выражение, из которого определяется минимальное значение d1,

 

где k — коэффициент, зависящий от профиля резьбы (для метрических резьб k = 1,3; для трапецеидальных k = 1,25); [σр] — допускаемое напряжение при растяжении для материала винта.

Если винт работает на сжатие, то его допустимая длина определяется из условия устойчивости при продольном изгибе по формуле

где E — модуль упругости материала винта; J = (pi*d1^4/64)*(0,4 + 0,6*(d/d1)) - приведенный момент инерции сечения винта; K1 = 0,5 – 2 - коэффициент, учитывающий жесткость конструкции опорных узлов. С увеличением жесткости значение K1, возрастает; K2 >=3 — коэффициент запаса устойчивости.

Расчет винта на продольную устойчивость целесообразно проводить при условии L/d2 >= 15 - 20.

В винтовых механизмах целесообразно применение смазочного материала, так как это обеспечивает высокий КПД. Если на рабочих боковых поверхностях резьбы давление будет превышать допустимое, смазочный материал будет выдавливаться, КПД резко уменьшится, возникнут местные задиры поверхности. Поэтому элементы резьбы винтовых механизмов проверяют на износостойкость

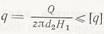
Допустимые значении износостойкости для средних давлений приведены ниже.

Материал [q], МПа

Сталь по чугуну...........................................................................................4—5

Сталь по антифрикционному чугуну.......................................................10—12

Сталь по бронзе...........................................................................................7—9

Закаленная сталь по бронзе......................................................................10—12

При значительных нагрузках Q выбранная резьба должна быть проверена на срез, смятие и изгиб.

Рассмотрим действие осевой силы Q/z (где z — число рабочих витков) на развернутый виток резьбы (рис. 73).

Запишем следующие основные уравнения прочности:

а) при деформации среза

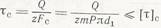
где mР — толщина ниток резьбы в сечении среза; m — коэффициент, зависящий от профиля резьбы (для трапецеидальной, резьбы m = 0,64; для метрической m = 0,78); Fс — площадь среза; [τ]c – допустимые напряжения среза;

б) при деформации смятия

где Fсм — площадь смятия; [σн] - допустимые напряжения смятия;

в) при деформации изгиба

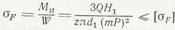
где W – момент сопротивления; [σF] – допустимые напряжения изгиба.

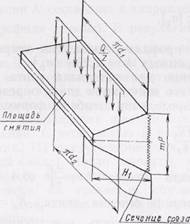
Рис. 73. Распределение нагрузок, действующих на виток.

Необходимо отметить, что на практике элементы резьбы проверяют на прочность только в крепежных деталях.

Особенности проектирования кинематических винтовых механизмов. Кинематические механизмы предназначены для точного перемещения отдельных узлов приборов, регулировки их взаимного положения. Кинематические механизмы используют также в качестве отсчетных устройств.

В этом случае для оценки точности их функционирования рассчитывают кинематическую погрешность и значение мертвого хода. При этом под кинематической погрешностью понимают максимальную разность погрешностей положения ведомого звена (δφmax - δφmin) (рис. 74). Мертвым ходом винтовой передачи называют разность положений ведомого звена для одинаковых положений ведущего при прямом и обратном ходах (рис. 74).

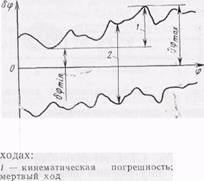
Рис. 74. Погрешность положения ведомого звена при прямом и обратном ходах.

Согласно ГОСТ 21098 — 82 минимальное и максимальное значения кинематической погрешности (при расчете методом максимума-минимума) могут быть оценены по формулам

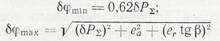
и мёртвого хода – по формулам

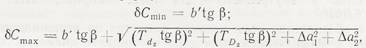
где δP∑ — накопленная погрешность шага резьбы, определяемая как разность между действительным и номинальным расстояниями между профилями витков по среднему диаметру на длине свинчивания (длине гайки), мкм; er и eα — соответственно радиальное и осевое биения витков, мкм; β — половина угла профиля резьбы (15° — в трапецеидальной и 30° - в метрической); Td2 - допуск среднего диаметра винта, мкм; TD2 - допуск среднего диаметра гайки, мкм; b' - верхнее отклонение среднего диаметра винта, мкм; Δа1, Δа2— осевые зазоры в опорах вращения, мкм.

При расчете вероятностным методом умножают величины δφmax и δCmax на коэффициент фазовой компенсации Кp, принимаемый в зависимости от заданного процента риска р:

P, %……………… 32 10 4,5 1,0 0,27

Kp……………… 0,76 0,80 0,86 0,96 0,98

Допуски метрических и трапецеидальных резьб регламентированы стандартами ГОСТ 16093—81 и ГОСТ 9562—81 (СТ СЭВ305—76, СТ СЭВ 306—76) и назначаются на наружный диаметр болта, внутренний диаметр гайки и на их средние диаметры. Допуском на средний диаметр ограничиваются и действительные отклонения половины угла профиля и шага резьбы, поэтому отдельно они не устанавливаются. Для наружного, внутреннего и среднего диаметров резьбы стандартом введены ряды основных отклонений, обозначаемые буквами латинского алфавита: строчной h, g, e, d, ... — для винта; прописной Н, G, E, D, ... — для гайки. Допуск каждого из диаметров определяется степенью точности (1, 2, ..., 12).

Обозначение поля допуска диаметра резьбы состоит из цифры, показывающей степень точности, и буквы, обозначающей основное отклонение.

Обозначение полей допусков резьбового соединения состоит из обозначения поля допуска среднего диаметра, помещаемого на первом месте, и обозначения поля допуска наружного диаметра для болтов и внутреннего — для гаек, например М12—7h6g; М12 — 5H6H.

Если обозначение поля допуска диаметра по вершинам резьбы совпадает с обозначением поля допуска среднего диаметра, то оно не повторяется (Ml2 — 6g).

Передаточное отношение идеального винтового механизма может быть определено как отношение поступательного перемещения винта или гайки к соответствующему вращательному:

i пост, вр = n*P/(2*pi)

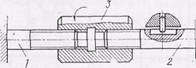
Рис. 75. Дифференциальный винтовой механизм.

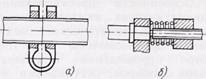
Рис. 76. Винтовые механизмы:

а – с упругой специальной гайкой, б – с пружинной для выбора зазора.

Для увеличения точности перемещений во многих узлах прецизионных приборов применяют дифференциальные винтовые механизмы с малым передаточным отношением. Дифференциальный винтовой механизм (рис. 75) состоит из двух соосных винтов 1 и 2 с различными шагами P1и P2 резьбы. В этом случае линейное перемещение выходного винта 2 за один оборот ведущего звена — гайки 3 будет P1 - P2, а передаточное отношение для однозаходных винтов

i пост, вр = (P1 – P2)/(2*pi).

Для уменьшения мертвых ходов в винтовых механизмах применяют конструкции гаек с упругим поджатием (рис. 76, а) или вводят специальные пружины, обеспечивающие постоянное направление осевых сил в механизме (рис. 76, б).