| Расчет и конструирование основных элементов цилиндрических прямозубых передач.
Геометрический расчет.
Основные параметры зубчатых колес и передачи определяют по модулю и числу зубьев колес.
Для цилиндрических прямозубых колес диаметр делительной окружности:d = mz.
Для колес наружного зацепления, нарезанных без смещения зуборезного инструмента, когда делительная окружность колеса катится без скольжения по средней линии профиля инструмента, диаметр окружности вершин зубьев:
da = d + 2m = mz + 2m = m (z + 2); диаметр окружности впадин df = d- 2,5m = mz — 2,5m = m (z - 2,5);
межцентровое расстояние а = (d1 + d2)/2. Выражая диаметры делительных окружностей через модуль и число зубьев, получим: a = 0,5m(z1+z2). Толщина зуба по делительной окружности (без учета бокового зазора): st = πm/2.
Силовой и прочностной расчеты.
В устройствах вычислительной техники, роботах и приборах используются кинематические и силовые зубчатые передачи, которые работают в принципиально различных условиях. Кинематические передачи (например, в механизме поворота шкалы прибора) практически не нагружены внешними силами, но в процессе работы здесь возникают крутильные и изгибные колебания. Расчеты таких передач выполняются на износостойкость.
Поломки зубьев силовых передач чаще всего возникают вследствие усталости материала; образуются микротрещины, которые постепенно увеличиваются. Интенсивность развития усталостных явлений зависит в первую очередь от уровня напряжений в зубьях, подвергающихся деформации изгиба и смятия в зоне контакта. При недостаточной прочности происходит быстрый износ и разрушение зубьев. Для предотвращения отмеченных явлений и обеспечения высокой надежности и необходимой долговечности передач проводят расчет зубчатых колес на прочность с учетом усталостных явлений.
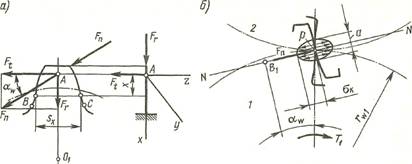
Рис.1
Возможны два вида расчета: проектный и проверочный. При проектном расчете обычно определяют один из следующих параметров: межосевое расстояние aw, диаметр делительной окружности d или модуль зацепления m. Проверочный расчет предусматривает определение по заданным нагрузкам и размерам колеса (найденным на основании геометрического расчета) наибольших контактных и изгибных напряжений, сопоставление их с допускаемыми.
Основной режим нагружения зубьев — циклический; поэтому далее приведены зависимости для расчета зубьев передач на выносливость по контактным и изгибным напряжениям. Зубчатые передачи вычислительных систем и приборов часто выполняются открытыми, работают в условиях полусухого трения. Это приводит к значительному износу, который обычно опережает процесс усталостного выкрашивания поверхности зуба. Поэтому для открытых передач, прежде всего, выполняется расчет на изгиб. Для передач, работающих при жидкой смазке, основной расчет — на контактную выносливость.
Расчет зубьев на изгиб. Цель расчета обеспечить выносливость зуба при изгибе, т. е. предотвратить его усталостный излом. В первом приближении зуб рассматривают как балку, защемленную одним концом. Наиболее опасно положение зуба в том случае, когда нагрузка Fn действует на вершину зуба, что соответствует моменту начала или конца зацепления пары сопряженных зубьев. Окружная составляющая Ft вектора Fn перпендикулярна оси зуба и вызывает его изгиб. Радиальная составляющая Fr, направленная вдоль оси зуба к центру колеса, сжимает зуб.
При совместном действии этих деформаций трещины возникают на растянутой стороне зуба; расчетное напряжение в сечении на расстоянии х от точки А:
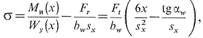
где Mи(x) = Ftx— изгибающий момент в рассматриваемом сечении; Wy(x) = bwsx2/6— осевой момент сопротивления сечения, прямоугольного в плане; bw—ширина зубчатого венца; sx— переменная по высоте толщины зуба; bwsx — площадь сечения зуба. Максимальное значение функции определяют с помощью ЭВМ. Если для опасного сечения ВС, в котором напряжение достигает наибольшего значения, обозначить
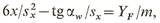
то искомое опасное напряжение:
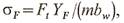
где расчетная окружная сила:
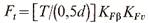
(Т—крутящий момент на данном звене, Н мм; KFβ — коэффициент, учитывающий неравномерность распределения нагрузки по длине зуба; KFv — коэффициент динамичности). Окончательный вид формулы проверочного расчета
для шестерни:
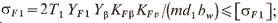
для колеса:
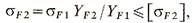
где dl = mzl /cos β-делительный диаметр (β—делительный угол наклона зубьев); bw = ψbddl—рабочая ширина зубчатого венца; ψbd— коэффициент ширины венца, 0,1<ψbd<0,5, (причем меньшие значения принимаются для консольно посаженных колес или расположенных несимметрично относительно опор); YF — коэффициент, учитывающий влияние формы зуба, для внешних зубьев:
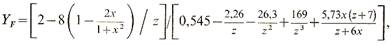
где z — число зубьев, для косозубых колес вместо z в формулу подставляется эквивалентная величина zэ = z/cos3β; x — коэффициент смещения.
Значение коэффициента динамичности KFv ориентировочно можно принять равным 1,1 для быстроходных (v =0,5 м/с) колес высокой точности (6-я или 7-я ступень); для колес менее точных или при ударной нагрузке KFv=1,2..1,3. Допускаемое напряжение:
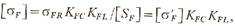
где σfr — предел выносливости при изгибе, для углеродистых и легированных сталей при твердости поверхности зуба <350 НВ; KFс=1 для нереверсивных KFс = 0,65 для реверсивных передач; KFL— коэффициент долговечности NF0— базовое число циклов напряжений; NE—действительное число циклов; n — частота вращения, об/мин; L — долговечность передачи, в среднем 5000... 10 000 ч; [SF] — коэффициент безопасности, равный 2,2, а для особо ответственных передач — 2,5; ориентировочные значения величины [σ'F] приведены в таблице. При расчетах число зубьев z1 шестерни назначают с учетом следующих соображений. При нарезании зубьев без смещения червячной фрезой с углом исходного контура α=20° (наиболее распространенный способ) для предотвращения подреза ножки зуба число зубьев должно быть не менее 17; при укороченных зубьях (ha+ =0,8), а также для несиловых передач можно допустить zmin = 14. Дальнейшее уменьшение возможно лишь при использовании колес, нарезанных со смещением.
Для обеспечения необходимой плавности хода, что особенно важно в быстроходных передачах, число зубьев шестерни рекомендуется назначать в зависимости от частоты вращения n.
Если шестерня и колесо изготовлены из одинакового материала, то проектный расчет передачи на прочность ведут по шестерне, так как ее зубья нагружаются в и раз чаще по сравнению с зубьями колеса [u — передаточное число]. Модуль зацепления вычисляют по формуле:
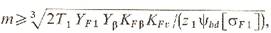
которая непосредственно следует из неравенства.
Проектный расчет выполняется по той же формуле и в случае, когда колесо изготовлено из менее прочного материала, чем шестерня; если Yt / [σF1]<Y2/ [σF2], то в подкоренное выражение вместо Yl/[σFl] подставляется отношение Y2l/[σF2].
Расчет зубьев по контактным напряжениям. Цель этого расчета— предотвратить усталостное выкрашивание поверхностей зубьев, т. е. обеспечить контактную выносливость зубьев. В качестве расчетного примем положение пары зубьев шестерни 1 и колеса 2 в зоне полюса зацепления (когда в зацеплении находится только одна пара зубьев). Зуб шестерни действует на зуб колеса силой Fn, которая направлена вдоль линии зацепления (нормаль NN к профилям зубьев). В результате деформации объемного смятия поверхностных слоев зубьев образуется контактная площадка размерами а и l3 (l3 — длина зуба, равная ширине bw венца прямозубого колеса). Из общей формулы следует условие прочности зуба:
Расчетная нагрузка на зуб:
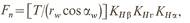
где Т—крутящий момент на валу, Н мм; КНβ, KHv — коэффициенты, аналогичные по физическому смыслу коэффициентам KFβ, KFv, использованным при расчетах на изгиб; коэффициент КНа учитывает влияние погрешностей зацепления с ростом окружной скорости.
Приведенный модуль упругости:
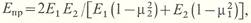
где Е1, μ1 и Е2, μ2 — модули упругости и коэффициенты Пуассона шестерни 1 и колеса 2 соответственно. Приведенный радиус кривизны:
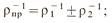
знак плюс — при касании выпуклых профилей (внешнее зацепление), знак минус — при касании выпуклого и вогнутого профилей (внутреннее зацепление). Из свойств эвольвенты следует, что радиусы кривизны для расчетной точки Р:
поэтому приведенный радиус кривизны для внешнего зацепления:
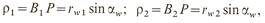
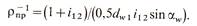
Зависимость для проверочного расчета на контактную выносливость получим, подставив в исходную формулу найденные величины и введя коэффициент zε для учета влияния степени перекрытия ε:
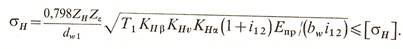
Формулы для расчета параметров приведены в таблице. Контактные напряжения в зубьях шестерни и колеса одинаковы и определяются левой частью неравенства. Поэтому при расчете колеса, когда оно выполнено из менее прочного материала, в условии прочности изменяется лишь значение допускаемого напряжения, которое рассчитывается по формуле:
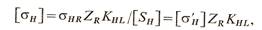
где σHR — предел контактной выносливости; ZR-коэффициент учитывающий влияние шероховатости поверхности зубьев.
Выразив через модуль величины dwl=mz1, bw = ψbdmz1, получим формулу для проектного расчета зубчатой передачи:
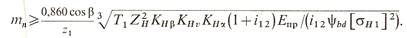
Так как на этапе проектного расчета величина s неизвестна, то коэффициент Zε принят равным единице, что идет в запас прочности. Как и при расчетах на изгиб, в формулу подставляются параметры шестерни, зубья которой испытывают в u раз большее число циклов. Если же рассчитывается колесо, то по аналогии с проверочным расчетом на контактную выносливость в выражение подставляется допускаемое напряжение для материала колеса, а параметры T1, z1 остаются без изменения. Если зубчатая передача работает в условиях обильной смазки, то ее рассчитывают по контактным напряжениям, а расчет на изгиб в этом случае проверочный. Передачи, работающие в условиях ограниченной смазки или совсем без смазки, рассчитывают только на изгиб.
Давление между рабочими поверхностями зубьев передается по общей нормали к их профилям. Если к ведомому колесу 2 приложен момент сопротивления Т2, то условная сосредоточенная сила давления зуба шестерни 1 на зуб колеса 2: Fn12 = T2/rb2 = T2/ (r2 cosα). Так как действие равно противодействию, то сила давления зуба колеса 2 на зуб шестерни 1: Fn21=-Fn12; Fn21=Fn12=Fn. Необходимый вращающий момент на ведущем валу (без учета потерь):
T1= Fn r1 cosα = (T2/ r2 cosα) (r1 cosα);
T1= T2 r1/ r2= T2 z1/ z2; T1= T2 / u, откуда
С учетом потерь (η12 = 0,96 ÷ 0,98) получим: T1= T2 / (u η12).
Для удобства расчетов силу Fn раскладываем на две составляющие:
Ft = Fn cosα и радиальную Fr = Fn sinα или Fr = Ft tgα.
При проектировании передач обычно задают значение Т2 и по нему определяют Ft=2T2/d2. Если задан движущий момент T1, то Ft=2T1/d1. При расчете зубьев по напряжению изгиба сжимающее радиальное усилие обычно не учитывают и рассматривают наиболее опасный случай, когда вся нагрузка приходится на один зуб и приложена к его вершине. Так как все размеры зуба определяются модулем, выражаем плечо силы h и толщину зуба у корня s через модуль: h =c1m и s = c2m.
Напряжение изгиба у корня зуба: σF = MF/WF. Изгибающий момент: MF = F1h= F1c1m
Момент сопротивления изгибу: WF = b s2/6= b (c2 m) 2/6, где b — ширина венца зубчатого колеса; с1 и с2 — коэффициенты пропорциональности.
Подставляя МF и WF в исходное уравнение, получим σF = 6 F1c1m/ b (c2 m) 2= Ft/bm =6c1/ c22
Величину 6c1/ c22называют коэффициентом формы зуба и обозначают YF. Значение YF определяют по таблицам или графикам в зависимости от числа зубьев и коэффициента смещения инструмента.
Величину нагрузки умножают на коэффициент kFv = 1,1÷1,5, учитывающий дополнительные динамические нагрузки в зацеплении, и коэффициент γ=1÷2, учитывающий абразивный износ (истирание) зубьев. Для закрытых передач, работающих в условиях обильной смазки, γ =1. Окончательно: σF= YF kFv γ Ft/bm.
В правильно спроектированных передачах рабочее напряжение изгиба должно быть меньше или равно допускаемому: σF 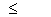 [ σF]. При расчете на усталость: [ σF]= (σF0 lim b /[SF]) kFl [ σF]. При расчете на усталость: [ σF]= (σF0 lim b /[SF]) kFl
где— σF0 lim b предел выносливости при отнулевом цикле нагружения; kFl — коэффициент долговечности,
1 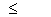 kFl kFl 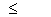 2,08;— коэффициент запаса прочности. 2,08;— коэффициент запаса прочности.
Для вывода формулы проектного расчета сделаем преобразования: Ft=2T2/mz2; b=ψmm
Где ψm = 3 ÷20 — коэффициент ширины (в приборах ψm = 3÷5). Подставляем Ft и b в уравнение и решаем его относительно модуля.
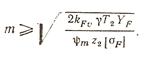
Расчет на прочность рабочих поверхностей зубьев ведется по преобразованной формуле Герца.
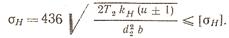
Выражая ширину зубчатого венца b через aw и коэффициент ширины зубчатого венца ψa: b= ψa a, заменяя d2 межосевым расстоянием d2 =2 aωu/u ± 1, получим формулу для проектного расчета прямозубых передач:
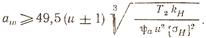
В формулах приняты следующие размерности: aw — межосевое расстояние, мм; Т2 — вращающий момент на ведомом валу, Н-мм; d2 — диаметр делительной окружности ведомого колеса, мм; b — рабочая ширина колеса, мм; σH — рабочее и допускаемое контактные напряжения, МПа. Знак «+» ставится при наружном зацеплении, знак «—» при внутреннем.
Допускаемое контактное напряжение [σH] определяют по формуле:
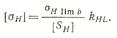
Где σH1limb — предел контактной выносливости при базовом числе циклов, для улучшенных и нормализованных сталей σH1limb = (2НВ +70), МПа; kHL — коэффициент долговечности, если число циклов нагружения каждого зуба больше базового, то kHL = 1. Когда число циклов нагружения меньше базового, то kHL вычисляют по формуле:
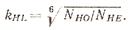
Модуль зацепления.
Расстояние между соответствующими точками двух соседних зубьев, измеренное по начальной окружности диаметра dw, называется начальным шагом pw. Если число зубьев колеса z, то длина окружности, по которой измерен шаг, zpw = πdw, а ее диаметр: dw = zpw/π.
Отношение pw/π=m называется модулем. Для ограничения количества зуборезного инструмента модули стандартизованы.
Модуль, измеряемый в мм,— основной параметр зубчатого зацепления, с помощью которого определяют размеры передачи.
Геометрические элементы.
Стандартным значение модуля будет лишь для одной окружности, которая называется делительной; диаметр делительной окружности (делительный диаметр): d=mz.
Элемент зуба, расположенный с внешней стороны делительной окружности, называется делительной головкой зуба, а с внутренней стороны этой окружности - делительной ножкой зуба. В точной механике чаще всего используется зацепление колес, в котором делительные и начальные окружности совпадают.
Для зацепления, широко применяемого в точной механике, размеры элементов шестерни и зубчатого колеса могут быть найдены по следующим зависимостям:
высота делительной головки зуба ha = ham; высота делительной ножки зуба hf = (ha+c*)m ;
радиальный зазор с = с*m; начальный диаметр dw= d = mz;
диаметры вершин и впадин da= d+ ha= m(z+2 ha) ;df = d-2hf = m[z-2( ha*+c*)];
радиус галтели pf = pf *m;
межосевое расстояние aw = 0,5(dwl + dw2) = 0,5m(zl+z2), где h*a — коэффициент высоты головки зуба (для нормальных зубьев h*a =1, для укороченных h*a = 0,8); с* — коэффициент радиального зазора (если ha=1, то для m≥1 с* = 0,25; для 0,5≤m<1 с* = 0,35; для 0,l≤m<0,5 с* = 0,4); коэффициент р f равен 0,384 при m≥1, 0,38...0,44 при m<1.
Для аналогичного внутреннего зацепления цилиндрических колес геометрические размеры колеса с внутренними зубьями нормальной высоты могут быть найдены по формулам:
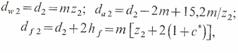
Так как в этой передаче зубья шестерни имеют выпуклый профиль, а колеса — вогнутый, то нагрузочная способность передачи внутреннего зацепления больше, чем при внешнем зацеплении. Кроме того, при прочих равных условиях передача внутреннего зацепления обладает большей плавностью и обеспечивает лучшие условия образования слоя смазки между зубьями. Однако изготовление колес с внутренними зубьями сложней, чем с внешними.
ПЕРЕДАТОЧНОЕ ОТНОШЕНИЕ. ОСНОВНАЯ ТЕОРЕМА ЗАЦЕПЛЕНИЯ
Передаточным отношением какого-либо механизма принято называть отношение угловых скоростей со входного и выходного звеньев этого механизма. Начальные окружности пары сопряженных колес перекатываются друг по другу без скольжения благодаря наличию зубьев; скорости vPl и vP2 точки Р, принадлежащей соответственно шестерне 1 и колесу 2, равны друг другу. С учетом формулы получаем выражение для передаточного отношения от шестерни 1 к колесу 2.
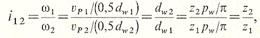
Для силовых цилиндрических прямозубых передач значение передаточного числа и, как правило, не превышает 7, а для передач приборов wmax = 8...12. В быстроходных передачах в целях снижения динамических нагрузок и вибраций в зацеплении рекомендуется назначать для u не целые числа (с тем, чтобы одни и те же зубья шестерни и колеса встречались в зацеплении как можно реже).
Для многоступенчатых зубчатых передач общее передаточное отношение iобщ определяется по формуле:
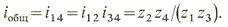
Выбор числа ступеней.
При проектировании привода с заданным общим передаточным отношением iобщ встает важная инженерная задача — выбор оптимального числа ступеней передач и распределение iобщ между отдельными ступенями. Это может быть сделано с учетом соблюдения условий обеспечения наименьших габаритных размеров всего механизма или получения наименьшего приведенного к ведущему валу момента инерции. При выбранных передаточных отношениях числа зубьев шестерен можно назначить в соответствии с требованиями к механизму. Это достаточно сложная и многовариантная задача, которая достаточно корректно решается только с помощью ЭВМ. Критериями оптимизации служат габаритные ограничения' минимизация массы, приведенного момента инерции или угловой погрешности.
Основная теорема зацепления.
Условие нормальной работы зубчатой передачи с круглыми колесами — обеспечение постоянного передаточного отношения. Это возможно лишь при определенном очертании сопряженных профилей зубьев шестерни и колеса. Пусть, например, шестерня 1 и колесо 2 находятся в зацеплении; rwl и rw2—радиусы их начальных окружностей. Линии NN и КК—нормаль и касательная в точке С соприкосновения профилей зубьев шестерни и колеса: vcl┴OlC и vC2┴O2C скорости точки С, принадлежащей зубу шестерни 1 и зубу колеса 2 соответственно.
Суть основной теоремы зацепления состоит в том, что для обеспечения условия i = const сопряженные профили зубьев должны быть очерчены такими кривыми, у которых нормаль NN в любой точке С взаимного касания зубьев всегда проходит через постоянную точку Р на линии центров колес O1O2.
Силы в зацеплении прямозубой передачи.
В точке С контакта зубьев действует нормальная к профилю зуба сила Fn; ее линия действия — линия зацепления NN, которая нормальна к профилям соприкасающихся поверхностей. Для ведомого колеса сила Fn создает момент T=Fnrw cosαw, направленный в сторону вращения; для ведущего колеса направление силы Fn противоположно.
По линии KK┴NN действует сила трения Ff = f Fn, где f—коэффициент трения скольжения.
ОСНОВЫ ТЕОРИИ ИЗГОТОВЛЕНИЯ ЗУБЧАТЫХ КОЛЕС И РАСЧЕТ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ ПРЯМОЗУБОЙ ЦИЛИНДРИЧЕСКОЙ ПЕРЕДАЧИ
Различают два способа образования зубьев: копирование и огибание. При копировании профиль инструмента представляет собой точную копию изготовляемого зубчатого колеса (или его части). В приборостроении по способу копирования изготовляют зубчатые колеса штамповкой. Недостаток этого способа — относительно низкая точность получаемых параметров зацепления.
Способ огибания (обкатывания) основной как в общем машиностроении, так и в приборостроении. Достоинства метода: высокая точность, одним инструментом данного модуля нарезают колеса с разными числами зубьев, большая производительность и возможность автоматизации процесса.
Большую часть зубчатых колес в настоящее время изготовляют нарезанием. Инструментом может служить инструментальная зубчатая рейка 1 с прямолинейным профилем зубьев или колесо с эвольвентными зубьями, называемое долбяком. Зуб рейки представляет собой равнобокую трапецию со скругленными углами вершин и впадин.
Параметры режущего инструмента — рейки—стандартизованы и определяются производящим исходным контуром; основные параметры рейки — угол профиля α, коэффициент высоты головки ha* и коэффициент радиального зазора с*.
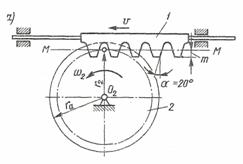
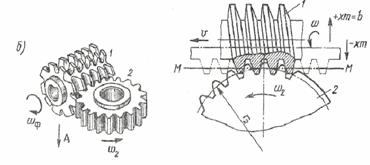
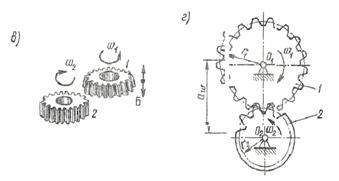
Рис.5
Линия ММ, по которой толщина зубьев равна ширине впадины, называется делительной прямой.
С кинематической точки зрения инструментальная рейка аналогична рейке зубчато-реечного зацепления. При нарезании зубьев рейкой воспроизводится такое относительное движение заготовки и рейки, как и при работе реечного, В процессе нарезания рейка 1 движется с небольшой скоростью v прямолинейно, а заготовка 2, предварительно обточенная по радиусу rа, вращается с угловой скоростью:
ω2= v/ (0.5mz2)
Режущее движение рейки — возвратно-поступательное, параллельное оси заготовки (перпендикулярно плоскости чертежа); при движении в одном направлении срезается часть материала заготовки, обратный ход — холостой.
Зубчатые колеса можно изготовить также долбяком 1,который в принципе является зубчатым колесом с режущими кромками. Долбяком можно нарезать колеса с внутренними зубьями, которые нельзя получить, используя инструментальную рейку.
Одной из перспективных разновидностей нарезания колес методом огибания является накатка зубьев, которую применяют в основном при изготовлении мелкомодульных колес. Инструментом служит зубчатое колесо 1 с числом зубьев z1 и модулем m; заготовка 2 выполнена из более мягкого материала, чем инструмент 1. В процессе образования зубьев относительные движения инструмента и заготовки такие же, как если бы в зацеплении находились обычные зубчатые колеса: инструмент вращается с угловой скоростью ω1з а заготовка — со скоростью ω2=ω1z1/z2, где z2 — получаемое число зубьев колеса-заготовки. В результате инструмент 1 выдавливает на заготовке 2 зубья соответствующего профиля; число зубьев определяется соотношением ω2/ ω1 и может быть любым. Разогрев заготовок колес с модулем m>0,8мм часто осуществляется токами высокой частоты.
Изготовление и применение колес со смещением инструмента. При изготовлении зубчатых колес делительная прямая инструментальной рейки может касаться делительной окружности колеса или отстоит от этой окружности на расстояние b =хm (х— коэффициент смещения). Если делительная прямая не пересекает делительную окружность, то коэффициент х считается положительным; в противном случае х <0.
Рис.6
Колеса, зубья которых образованы при х = 0, носят название колес без смещения. При х ≠0 получают зубчатые колеса со смещением. Выбирая определенные коэффициенты смещения, можно в широких пределах управлять качественными характеристиками передачи. Габариты зубчатой передачи определяются ее межосевым расстоянием, которое зависит от модуля зацепления m, передаточного отношения i и числа зубьев z1 шестерни. Значение модуля обусловлено прочностью зубьев и технологическими условиями, а передаточное отношение — кинематикой привода. Следовательно, сокращение габаритов передачи может быть достигнуто уменьшением числа зубьев z1 шестерни. При нарезании рейкой колес с коэффициентом х=0 и числом зубьев z <zmin = 17 (при α = 20° h*a = 1) зубья получаются подрезанными ниже точки А эвольвентный профиль срезается и прочность ножки зуба уменьшается; кроме того, уменьшается степень перекрытия зацепления. Чтобы устранить подрезание, режущий инструмент отодвигают от центра заготовки на размер b. Если смещение применено для предотвращения подрезания ножки зуба, то коэффициент х1 шестерни определяют из условия: х1= h*a (zmin —z1)/zmin где h*a — коэффициент высоты головки зуба; z1 — нарезаемое число зубьев; zrnin = 2 h*a /sin2α— наименьшее число зубьев, при котором нет подрезания.
Проектируя передачу, можно за счет выбора коэффициентов х1 и х2 повысить ее контактную прочность и выносливость — при максимальном коэффициенте суммы смещений xΣ = x1+x2. Увеличение изгибной прочности достигается таким подбором коэффициентов смещения, при которых коэффициент формы зуба YF максимален. Можно создать наиболее износостойкую передачу, так как соответствующий выбор коэффициентов х1<2 уменьшает скольжение профилей или делает его более равномерным (тогда при износе не искажается исходная форма эвольвенты зуба).
При выборе значений коэффициентов смещения нужно обеспечить условия существования данной передачи. Коэффициент перекрытия должен быть больше минимально допустимого, подрезания зубьев не должно быть, толщина зуба на окружности вершин Sta≥0,25m для кинематических передач и Sta≥0,4m для силовых, необходимо избежать интерференции зубьев, когда профили «накладываются» друг на друга и передача заклинивается.
Наиболее удобным методом выбора коэффициентов смещения, учитывающим все указанные условия, является метод «блокирующих контуров».
Если известны (выбраны) коэффициенты смещения, то параметры передачи рассчитываются по формулам:
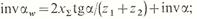
межосевое расстояние
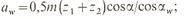
радиусы начальных окружностей
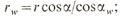
радиусы окружностей впадин
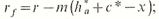
т. к. радиальный зазор в зацеплении должен быть равным c*m, то при известных x1,2 иaω радиусы окружностей
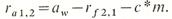
В некоторых случаях необходимо выполнить прямозубую передачу с точно заданным межосевым расстоянием aw при определенном модуле и числах зубьев. Тогда угол зацепления определяется из формулы, выбрав коэффициенты х1,2 так, чтобы величина хΣ была равна вычисленной по формуле, получим передачу с точно заданным межосевым расстоянием.
В приборостроении часто применяют так называемое равносмещенное зацепление, которое может быть осуществлено при условии z1+z2>2zmin. В этом случае относительный сдвиг для колеса х2 = —х1. Для равносмещенной передачи угол зацепления, радиусы начальных окружностей и межосевое расстояние aw равны соответствующим параметрам зацепления, составленного из колес без смещения.
КОНСТРУКЦИИ И МАТЕРИАЛЫ ЗУБЧАТЫХ КОЛЕС
Типовые конструкции мелкомодульных зубчатых колес показаны на рис. 14.6. Металлические зубчатые колеса получают путем механической обработки или штамповки заготовок с последующим нарезанием зуба. Колеса могут быть дисковыми, с односторонней или двусторонней ступицей. При разности размеров da -d1>18 мм в торцах дисков колеса могут делаться выточки и отверстия для снижения массы и момента инерции колеса. Число отверстий в диске равно 3 или 6 (в зависимости от размера колеса) диаметр отверстий —5... 10 мм. При относительно большом диаметре (da>80 мм) и необходимости применять цветной сплав или синтетический материал для изготовления зубчатого венца используется конструкция сборного колеса. В ряде механизмов применяют блоки зубчатых колес, свободно вращающихся на осях. У колес с малым числом зубьев
(шестерни или трибки) часто расчетный диаметр окружности впадин близок к диаметру вала. В этом случае зубья нарезают непосредственно на валу. Выбор материала для изготовления зубчатых колес обусловлен особенностями их работы.
Для цилиндрических и конических колес, работающих с небольшими окружными скоростями (до 3 м/с), обычно применяют качественные конструкционные стали марок 20...35; при повышенных окружных скоростях — сталь 45, 50, легированные стали 20Х, 40Х, 12ХНЗА и др. Для изготовления валов-шестерен и трибов применяют также инструментальные стали У8А, У10А.
С этой целью для изготовления шестерни выбирают более качественный материал или предусматривают упрочнение зубьев. Положительное качество цветных металлов — пониженные потери на трение.
В точных механизмах, в частности в механизмах ЭВМ, широко применяют зубчатые колеса из синтетических материалов. Эти материалы обладают высокой упругой податливостью (жесткость в 20...50 раз меньше, чем в передачах из металлических колес), износостойкостью, демпфирующей способностью, коррозионной стойкостью и другими свойствами, обеспечивающими плавную, бесшумную работу передач при высоких скоростях движения. Экспериментально установлено, что уровень шума полимерной и металлополимерной зубчатых передач на всех скоростных режимах значительно ниже уровня шума стальных колес. Кроме того, при выполнении шестерни из металла, а колеса — из синтетического материала хорошо гасятся динамические колебания и интенсивно отводится (через металлическую
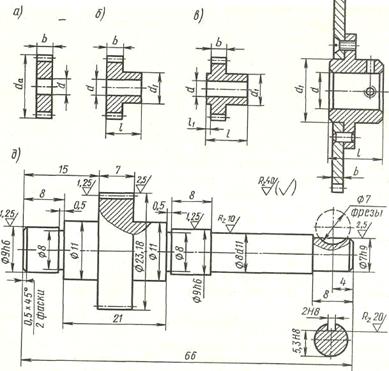
Рис.7
шестерню) теплота, образующаяся вследствие трения зубьев. При проектировании комбинированных передач ширину металлической шестерни назначают несколько больше ширины колеса, чтобы предотвратить неравномерный износ его зубьев по длине.
Момент инерции зубчатых колес из синтетических материалов в 4...5 раз меньше, чем у одинаковых по размерам металлических колес; следовательно, время разгона и выбега (остановки) механизма может быть значительно сокращено. Зубчатые колеса из синтетических материалов могут работать без смазки. При этом для повышения износостойкости зубьев и снижения коэффициента трения целесообразно перед сборкой выдержать колеса в масле. Геометрия зацепления и методика выбора основных параметров (числа зубьев, передаточного отношения, модуля) металлических и синтетических колес принципиально одинаковы.
<Вернуться в начало>
|