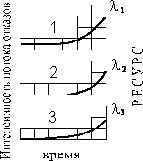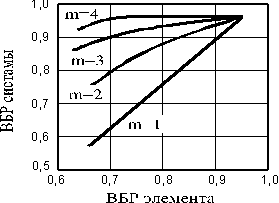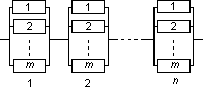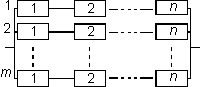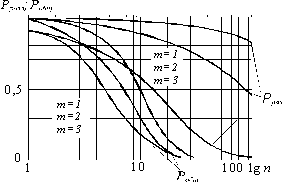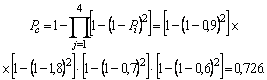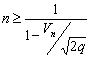ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Содержание:
Обеспечение надежности сельскохозяйственных машин при проектировании |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
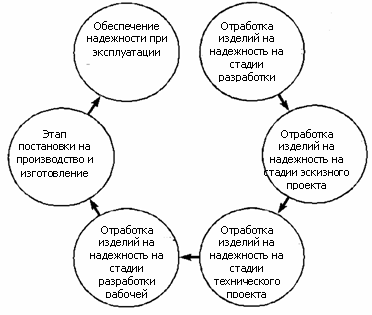
9.1. - Управление надежностью сельскохозяйственных машин. 9.2. - Общие понятия теории надежности. 9.3. - Показатели надежности сельхозмашин. 9.4. - Критерии отказов и предельных состояний. 9.6. - Повышение надежности систем за счет резервирования. 9.7. - Достижение заданного уровня надёжности элементов СХМ расчётными методами. 9.8. - Определение требуемой надёжности. 9.9. - Прогнозирование уровня надёжности элементов машин экспериментально-расчётными методами. 9.10. - Экспериментальная оценка уровня надёжности машин. 9.11. - Система проектирования несущих конструкций. 9.12. - Примеры и результаты расчета. 9.1. Управление надежностью сельскохозяйственных машинПод управлением надежностью СХМ в общем виде понимают совокупность скоординированных мероприятий по обеспечению рационального уровня показателей надежности машин в условиях рядовой их эксплуатации, при минимальных затратах на проектирование, в производстве и эксплуатации. Процесс управления надежностью машин сложен, многогранен, касается большого комплекса вопросов в сферах конструирования, испытания, производства, а также эксплуатации машин; он охватывает все стадии жизненного цикла. Этот процесс можно разделить на следующие этапы. 1. Выбор номенклатуры и численных значений показателей надежности. Это сложная технико-экономическая задача, решаемая комплексом исследовательских методов. 2. Нормирование ресурсов основных деталей, сборочных единиц и агрегатов, исходя из норм долговечности машины. 3. Конструкторское, расчетное, экспериментальное и технологическое обеспечение норм долговечности машины и её составляющих. 4. Испытание и доводка новых конструкционных решений до заданных показателей. 5. Разработка инструкций по эксплуатации, ремонту и контролю состояния машины. 6. Аттестация технического уровня машины. 7. Обеспечение стабильности и совершенствование изготовления серийно выпускаемых машин. 8. Авторский контроль за эксплуатацией в рядовых условиях и разработка мероприятий по обеспечению надежности машины. 9. Разработка стандартов по обеспечению надежности машины. Ряд рассмотренных этапов осуществляется одновременно, при этом они связаны между собой и дополняют друг друга. Таким образом, управление надежностью машин требует комплексного подхода, причем разработка и принятие каждого мероприятия должны учитывать все его технико-экономические последствия как в сфере производства, так и в сфере эксплуатации. Следует отметить, что среди перечисленных выше этапов обеспечения надежности каждый из них содержит некоторый объем экспериментально-исследовательских работ в виде эксплуатационных, полигонных или стендовых испытаний. Испытания являются одним из основных видов информации о надежности машин. Полученные при этом данные об уровне надежности конструкции и её зависимости от основных факторов, определяющих надежность, позволяют решать широкий круг вопросов управления качеством. К основным из них относятся: установление характеристик надежности, выявление слабых мест и разработка мероприятий по повышению их надежности, применение рациональной системы ремонта и технического обслуживания машины, определение эффективности и экономической целесообразности дальнейшей эксплуатации машины или агрегата, проверка достоверности расчетов и прогнозов, выполняемых при проектировании конструкционных элементов, а также оценки качества технологического процесса изготовления машины.
9.2. Общие понятия теории надежностиОсновные понятия и термины надежности стандартизированы, но многие стандарты при этом имеют лишь рекомендательный характер. Технический объект (объект) – предмет, подлежащий расчету, анализу, испытанию и исследованию в процессе его проектирования, изготовления, применения, технического обслуживания, ремонтов, хранения и транспортирования в целях обеспечения эффективности его функционального назначения. Механическая система (система) – сложный объект, представляющий собой совокупность взаимосвязанных и расположенных в определенном порядке объектов. В качестве таких систем рассматриваются машины, агрегаты, сборочные единицы, которые могут входить в более сложную систему как подсистемы или элементы. Элемент – это деталь, сборочная единица, агрегат и даже машина, если они в данной системе представлены только своими внешними параметрами. Надежность – свойство объекта выполнять и сохранять во времени заданные ему функции в заданных режимах и условиях применения, технического обслуживания, ремонтов, хранения и транспортирования. Надежность является внутренним свойством объекта, но проявляется во взаимодействии этого объекта с другими объектами. Общее число единичных и комплексных показателей надежности объектов, с помощью которых определяется количественная характеристика одного или нескольких свойств, составляющих в целом надежность исследуемой системы, используется более трех десятков. Изделие машиностроения в периоды его применения, хранения, транспортирования, технического обслуживания и ремонта в течение всего срока службы всегда находится в одном из следующих состояний: исправное состояние – состояние объекта, при котором он удовлетворяет всем требованиям нормативно-технической документации (НТД); неисправное состояние (неисправность) – состояние объекта, при котором значения всех параметров, характеризующих его способность выполнять заданные функции, не соответствуют требованиям НТД; неработоспособное состояние (неработоспособность) – состояние объекта, при котором значение хотя бы одного параметра, характеризующего его способность выполнять заданные функции, не соответствует требованиям НТД; предельное состояние – состояние объекта, при достижении которого его дальнейшее применение по назначению недопустимо или невозможно; повреждение – событие, заключающееся в нарушении исправности объекта при сохранении его работоспособности; отказ – событие, заключающееся в нарушении работоспособности объекта: ремонтируемый объект – объект, для которого возможность проведения ремонтов и технического обслуживания предусмотрена в НТД; неремонтируемый объект – объект, для которого возможность проведения ремонтов и технического обслуживания не предусмотрена в НТД; наработка – продолжительность или объем работы объекта; ресурс – наработка объекта от начала его применения до наступления предельного состояния; срок службы – календарная продолжительность эксплуатации объекта от начала его применения до наступления предельного состояния; срок сохраняемости – календарная продолжительность хранения и (или) транспортирования объекта в заданных условиях, в течение и после которых сохраняются исправность и основные показатели надежности в пределах, установленных НТД; оперативная продолжительность восстановления – время проведения операций по восстановлению работоспособности объекта, определяемого его конструкцией, техническим состоянием и приспособленностью к одновременному выполнению работ несколькими исполнителями; оперативная трудоемкость восстановления – сумма затрат времени всех участвующих исполнителей; оперативная стоимость восстановления – стоимость выполнения операций восстановления работоспособности объекта с учетом квалификации участвующих исполнителей.
9.3. Показатели надежности сельхозмашинСогласно ГОСТ 27.003-90 требования по надежности определяются как совокупность количественных и качественных требований к безотказности, долговечности, ремонтопригодности и сохраняемости, выполнение которых обеспечивает эксплуатацию объектов с заданными показателями эффективности [39]. В соответствии с нормативно-технической документацией по надежности машин к количественным показателям надежности относятся следующие: 1) безотказность (вероятность безотказной работы, параметр потока отказов, средняя наработка до отказа и наработка на отказ, g - процентная наработка); 2) долговечность (g - процентный и средний срок службы, g - процентный и средний ресурс); 3) ремонтопригодность (среднее время восстановления работоспособного состояния); 4) сохраняемость (средний срок сохраняемости, g - процентный срок сохраняемости); 5) комплексные показатели (коэффициент готовности, коэффициент технического использования). Показатели надежности сельхозмашиы и её составляющих частей выбираются в зависимости от этапа работ по обеспечению их надежности. После завершения этапа работ может возникнуть необходимость выбора других показателей надежности. При выполнении научно-исследовательских работ по повышению надежности рациональное использование нескольких показателей надежности, значения которых дополняют друг друга, позволяет эффективнее оценить успех проводимых работ. При обслуживании серийных сельхозмашин номенклатура показателей надежности сокращается до минимального количества. Процедура выбора номенклатуры показателей надежности состоит из трех этапов: 1. Выбор показателей безотказности, ремонтопригодности и комплексных показателей. 2. Выбор показателей долговечности. 3. Выбор показателей сохраняемости. Оценка ресурса сельхозмашин в основном определяется безотказностью и долговечностью.
9.3.1. Показатели безотказности элемента
Показатели безотказности машин приводятся в двух форматах: в вероятностной и статистической. Первая - удобна для аналитических расчетов, вторая - при экспериментальных исследованиях. Показатели безотказности восстанавливаемых и невосстановливаемых объектов во многом однотипны. Для оценки этих показателей необходимо рассмотреть следующие зависимости.
где Приведенные зависимости позволяют определить следующие показатели безотказности: 1. Вероятность безотказной работы на интервале времени от 0 до
на интервале времени от
Безотказность – свойство объекта сохранять работоспособность непрерывно, в течение некоторого времени пли некоторой наработки. Вероятность безотказной работы (ВБР) – это вероятность того, что в пределах заданной наработки отказ объекта не возникает. Если N(t) – число работоспособных объектов на момент наработки t, то, например, к моменту наработки t3 вероятность безотказной работы определяется: Р(t) = Р(0;t3) = 1– Q(0;t3), где N(0) – число работоспособных объектов при t = 0; Q(0;t3) – вероятность отказа за наработку от 0 до t3. Статистическая оценка вероятности безотказной работы за наработку t3 определяется:
где r(t3) – число отказавших объектов к моменту t3. Вероятность безотказной работы P(t) и вероятность отказа Q(t) образуют полную группу событий P(t) + Q(t) = 1. Тогда
где r(t1) – число отказавших объектов к моменту t1. При
Средняя наработка до отказа – это математическое ожидание объекта до первого отказа. Если Q(t) – функция распределения наработки объекта до первого отказа, то средняя наработка до отказа [39]
Наработка до второго отказа может иметь другую функцию Q(t). Параметр потока отказов – это характеристика восстанавливаемых объектов. Если каждый из N объектов (i = 1…N) имеет наработку до отказа Тi при этом у каждого ri отказов, то вся масса отказов å ri будет представлять собой поток отказов. Среднее число отказов за наработку Т
Применяя предельный переход при N ® ¥, получим математическое ожидание числа отказов за определенную наработку
где H(t) – характеристика потока отказов, т.е. число отказов за определенную наработку. Тогда скорость появления отказов, т.е. число отказов в единицу времени вблизи наработки t, можно определить как
Эта величина называется параметром потока отказов. В технике потоки отказов стараются свести к простейшим: стационарным, ординарным и не имеющим последствий. Стационарным называется поток, в котором число отказов не зависит от момента начала отсчета, а зависит только от величины наработки Dt = t2 – t1. Ординарный поток характеризуется тем, что за малый промежуток времени происходит не более одного отказа. Не имеющим последствий называют такой поток отказов, когда отказ одного элемента не вызывает отказ других элементов. Это условие не всегда выполнимо. Интенсивность отказов – это характеристика невосстанавливаемых объектов. Интенсивность отказов оценивает вероятность отказа за малый промежуток Dt времени работы (или наработки)
где Q (Dt) – вероятность отказа за время Dt. Если известна плотность вероятности отказов q (t) и закон распределения вероятности безотказной работы Р (t), то
Это выражение позволяет связать три главных характеристики и является одним из основных в теории надежности q (t) = l (t)×P (t). Для стационарных, ординарных потоков отказов без последствий понятия «параметр потока отказов» и «интенсивность отказов» совпадают. Таким образом, безотказность количественно характеризуется: вероятностью безотказной работы P(t); средней наработкой до отказа 9.3.2. Показатели долговечности
Долговечность - свойство объекта сохранять работоспособность до перехода в предельное состояние с возможными перерывами для технического обслуживания и ремонтов. Долговечность характеризуется продолжительностью работы объекта по суммарной наработке, прерываемой периодами для восстановления его работоспособности в плановых и неплановых ремонтах и техническом обслуживании. Для объекта процесс эксплуатации можно представить в виде схемы, представленной на рис. 9.1.
Рис. 9.1. Процесс эксплуатации машины
Количественно долговечность оценивается основными показателями: сроком службы; ресурсом. Срок службы – календарная продолжительность эксплуатации объекта от начала его применения до наступления предельного состояния. Ресурс – наработка объекта от начала его применения до наступления предельного состояния å ti. Срок службы учитывает не только рабочее время, но и время простоев, хранения, транспортирования. Гамма-процентный ресурс – наработка, в течение которой объект не достигает предельного состояния с заданной вероятностью g, выраженной в процентах. По достижении наработки Т, g% машин из парка останутся работоспособными. Для невосстанавливаемых объектов понятия ресурса и наработки на отказ совпадают. Для восстанавливаемых объектов значение наработки, для которой задана вероятность безотказной работы (ВБР) Р(t) = g% и есть g% – ресурс. Средний ресурс – математическое ожидание ресурса. Назначенный ресурс – ресурс, по достижении которого объект снимается с эксплуатации независимо от его состояния. Назначенный ресурс определяется по условиям безотказности или по экономическим соображениям. Аналогичными показателями характеризуется и срок службы: g% – срок службы (например, g = 80%, т.е. при достижении заданного срока службы 80% парка машин останутся работоспособными). 9.3.3. Показатели ремонтопригодности
Ремонтопригодность – свойство объекта, заключающееся в его приспособленности к предупреждению и обнаружению отказов и повреждений, к восстановлению работоспособности и исправности путем проведения технического обслуживания и ремонта. Свойство ремонтопригодности количественно характеризует компоновочное решение системы (машины, агрегата, сборочной единицы, детали), а также их доступность и легкосъемность. Для поддержания надежности машины в эксплуатации проводят техническое обслуживание (ТО). Для всей используемой техники принята система планово-предупредительного технического обслуживания (ППТО) и ремонтов. Плановость заключается в планировании ТО и ремонтов, а предупредительность в том, что ТО содержит операции, предупреждающие отказы. Правила ТО излагаются в инструкциях по эксплуатации машины. Существуют ежесменные – ЕТО, а также TO-1 и TO-2. ЕТО проводят перед началом каждой смены, то есть через 8-10 часов работы. Периодичность ТО-1 и ТО-2 определяется нормативно-технической документацией на машину, где указывается объем наработки (в часах или других показателях). Обычно после 2…5 ТО-1 выполняют ТО-2, а затем все это повторяется. В настоящее время проводится два вида плановых ремонтов: текущий и капитальный. Текущий ремонт характеризуется небольшим количеством сборочно-разборочных работ относительно низкой стоимости, возможностью проведения ремонта на месте без транспортирования машины на ремонтное предприятие. Суть этого ремонта заключается в замене недолговечных частей и восстановлении работоспособности отдельных агрегатов с помощью регулировки. Капитальный ремонт характеризуется большим объемом сборочно-разборочных корпусных деталей, применения специального оборудования в специализированных производственных условиях. Кроме плановых ремонтов, существуют внеплановые ремонты при отказах. Агрегатно-узловой метод ремонта заключается в замене отказавших агрегатов агрегатами из запасного фонда. Показатели ремонтопригодности определяются как затраты времени, труда и средств на выполнение операций по монтажу и демонтажу сборочных единиц, их сборке и разборке, а также выполнения сопутствующих подготовительных и заключительных операций. Эти затраты определяются при заданном наборе инструментов и приспособлений, квалификации операторов и условий выполнения работ. На все виды плановых ТО и ремонтов есть нормативы по затратам времени, труда и средств. Количественно ремонтопригодность оценивают: средним временем восстановления
где n – количество отказов, ТО, ремонтов; tb – время на восстановление (ТО, ремонта); вероятностью восстановления в заданное время Pb(t) – это вероятность того, что время восстановления не превысит заданное Тb; затратами времени, труда, средств на выполнение операций по восстановлению его работоспособности, на выполнение обслуживания оцениваются оперативными показателями; затратами на обслуживание и ремонт за определенную наработку объекта - оцениваются суммарными показателями; затратами на обслуживание и ремонт, приходящиеся на единицу наработки - оцениваются удельными показателями. 9.3.4. Показатели сохраняемости
Сохраняемость – свойство объекта непрерывно сохранять исправное и (или) работоспособное состояние в течение и (или) после режима ожидания, хранения и (или) транспортирования. Свойство сохраняемости характеризует способность объекта противостоять отрицательному влиянию факторов длительного его хранения или транспортирования и обеспечивать его применение после режима ожидания с заданными показателями функционирования с сохранением показателей безотказности и долговечности как объекта в целом, так и его элементов. Количественные характеристики этого показателя надежности аналогичны количественным характеристикам показателей долговечности (срок службы – срок сохраняемости). Срок сохраняемости – календарная продолжительность хранения и (или) транспортирования объекта в заданных условиях, в течение и после которых сохраняются исправность и основные показатели надежности в пределах, установленных НТД. Такими характеристиками являются: - гамма-процентный срок сохраняемости – календарная продолжительность хранения, в течение которой объект не достигнет предельного состояния (т.е. показатели безотказности, долговечности и ремонтопригодности не выйдут за установленные пределы) с вероятностью g, выраженной в процентах; - средний срок сохраняемости – математическое ожидание срока сохраняемости. Для машин, имеющих сезонное применение, значение этого показателя надежности очень велико. 9.3.5. Комплексные показатели надежности
Комплексные показатели характеризуют одновременно два и более свойств объекта. Наиболее широко используются такие показатели, как коэффициент готовности, коэффициент технического использования и коэффициент оперативной готовности. Коэффициент готовности – вероятность того, что объект окажется работоспособным в произвольный момент времени, кроме планируемых периодов, в течение которых применение объекта по назначению не предусматривается. Определяется он статистически
где tn – суммарная наработка n-го объекта в заданном интервале эксплуатации; tn – суммарная продолжительность восстановления работоспособности в заданном интервале эксплуатации; N – число наблюдаемых объектов. Коэффициент готовности оценивает надежность объекта на определенном интервале эксплуатации и является средней величиной на данном интервале. При нормировании этого показателя необходимо в НТД указывать интервал эксплуатации объекта, на котором его следует оценивать. Коэффициент технического использования – отношение математического ожидания наработки объекта за некоторый период эксплуатации к сумме математических ожиданий наработки, продолжительности технического обслуживания и ремонтов за тот же период эксплуатации. Обычно КТИ, определяется на базе ремонтного цикла
где ТР – наработка за некоторый период эксплуатации (например, до первого капитального ремонта); Если Коэффициент оперативной готовности – вероятность того, что объект окажется работоспособным в произвольный момент времени, кроме планируемых периодов, в течение которых применение объекта по назначению не предусматривается, и начиная с этого времени будет работать безотказно в течение заданного интервала времени.
где t0 – момент времени, с которого возникает необходимость применения объекта по назначению; t1 – момент времени, когда применение объекта по назначению прекращается; P(t0,t1) – вероятность безотказной работы объекта в интервале (t0;t1). 9.3.6. Показатели технико-экономической эффективности повышения надежности
Важным параметром оценки качества машин является оценка эффективного срока службы, под которым понимается продолжительность работы в средних условиях эксплуатации, после которого затраты средств на восстановление работоспособности машин возрастают настолько, а производительность их настолько снижается, что дальнейшее восстановление и эксплуатация экономически нецелесообразны. С увеличением срока службы машины эксплуатационные расходы возрастают, а степень их возрастания зависит от организации и качества технического обслуживания и ремонта машины. Главной причиной увеличения расходов на техническое обслуживание и ремонт машин является возрастание количества запасных и восстанавливаемых деталей, необходимых для замены изношенных. В настоящее время на ремонт машин расходуется металла в несколько раз больше, чем на изготовление новых, а стоимость ремонтов за срок службы в несколько раз превышает стоимость новой машины. Экономически целесообразный срок эксплуатации машины аналитически может быть установлен путем определения себестоимости продукции с учетом интенсивности нарастания расходов на техническое обслуживание и ремонты машины. Однако экономически целесообразный срок службы машины может быть значительно увеличен путем повышения надежности их за счет улучшения узлов и деталей, использования более надежных комплектующих элементов, автоматизации управления, регулирования и контроля за работой механизмов и рабочих органов, совершенствования условий эксплуатации, но это решается на основе технико-экономических сопоставлений. Экономическую эффективность сопоставляемых способов повышения надежности определяют сравнением основных стоимостных и натуральных показателей. Повышение уровня надежности сопряжено с повышением себестоимости машины, так как это связано с дополнительными расходами на проведение необходимых мероприятий. С другой стороны, эксплуатация более надежных машин обходится дешевле за счет сокращения затрат на ремонты и сокращения простоев по причинам отказов. При определении экономически эффективного срока службы машины следует учитывать ее моральный износ. Под моральным износом машины понимается срок службы, после которого конструкция машины технически и экономически неэффективна по сравнению с вновь выпускаемыми машинами для выполнения данных работ. При современном техническом прогрессе в машиностроении моральный износ часто опережает технический износ машины, что приводит к уменьшению срока ее службы и замене эксплуатируемой машины новой, более производительной и экономичной. Замена морально устаревшей машины, или ее модернизация, производится с учетом как затрат на приобретение новой машины, так и того экономического эффекта, который может быть получен при ее эксплуатации. Экономический метод анализа основывается на том, что затраты на изготовление и затраты на эксплуатацию машины или оборудования разделяют по их экономическим элементам и в зависимости от величины поэлементных затрат выбирают соответствующие основные показатели качества. Это позволяет также определять весомость отдельных показателей при оценке технического уровня качества. Выбор основных показателей качества на основе анализа затрат осуществляется на базе анализа себестоимости машин (оборудования) и себестоимости производимой продукции. Затраты изготовления и эксплуатации машины следует рассматривать по их укрупненным экономическим элементам. Себестоимость изготовления машины можно представить в виде формулы
где i = 1, 2, 3, … , n – количество укрупненных поэлементных экономических показателей; K1 – затраты на основные и вспомогательные материалы (включая полуфабрикаты и комплектующие изделия); К2 – затраты на заработную плату и социальные отчисления; К3 – затраты на энергию; К4 – затраты на содержание и обслуживание заводского оборудования; К5 – общезаводские затраты на освоение производства; К6– внепроизводственные затраты; Кn – другие затраты на изготовление, не учтенные в предыдущих. Себестоимость эксплуатации или суммарные затраты на эксплуатацию машины (единицы оборудования) за весь срок службы определяются как сумма
где C1 – расходы на заработную плату и социальные отчисления; С2 – затраты на электроэнергию, топливо, сжатый воздух и т.п; С3 – затраты на гидрожидкость, смазочные, обтирочные и другие материалы; С4 – расходы на техническое обслуживание и на все виды ремонтов (кроме капитального); C5 – отчисления в фонд амортизации, определяемые в соответствии с действующими нормами; С6 – косвенные затраты или потери из-за непредвиденных простоев; Сm – все остальные затраты на эксплуатацию, не учтенные в предыдущих. Определив средние значения суммарных и поэлементных затрат на изготовление и эксплуатацию, можно вычислить коэффициенты весомости всех поэлементных затрат. Коэффициенты весомости каждого вида поэлементных затрат С, определяют по формулам
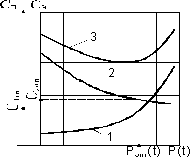
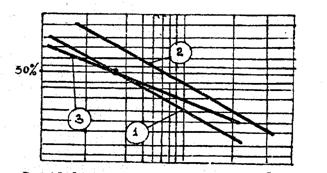
где 9.4. Критерии отказов и предельных состоянийС точки зрения требований надежности любое изделие может находиться в одном из двух состояний: быть работоспособным или неработоспособным. Событие, заключающееся в нарушении работоспособности изделия, называется отказом. Все критерии отказов можно разделить на три блока: - экономические; - технические; - параметрические. Экономическими критериями отказов могу служить прямые затраты по восстановлению работоспособности. Эти затраты выражаются через трудоемкость или стоимость, а также через косвенные потери производительности из-за вынужденных простоев, энергии, сырья, горючего, материалов или проявления недопустимых отклонений показателей качества продукции, производимой объектом, выраженных через экономический ущерб (от простоев техники) (рис. 9.2). Техническими критериями отказов являются недопустимые изменения геометрических форм элементов объекта (предельный износ пар трения, предельное значение деформаций, появление усталостных трещин), появление вибраций, шума и т.д., которые можно обнаружить и измерить. Параметрическими критериями отказов могут быть выходы параметров качества функционирования за установленные НТД пределы.
Рис. 9.2. Зависимость эксплуатационных и производственных затрат от условия надежности объекта: 1 - затраты на обеспечение уровня безотказности в производстве; 2 - затраты на поддержание уровня безотказности в эксплуатации; 3 - суммарные затраты 9.4.1. Классификация отказов
По частоте отказов различают единичные отказы и повторяющиеся п раз за определенный период наработки. По последствиям отказы разделяются на отказы функционирования и параметрические. Отказ функционирования заключается в том, что объект не может выполнять своих функций. Параметрический отказ заключается в выходе параметров объекта за допустимые пределы. По сложности устранения отказы объектов делятся на три группы: I – отказы устраняются в процессе технического обслуживания; II – отказы устраняются в процессе текущего ремонта; III – отказы устраняются в процессе капитального ремонта. По способности восстановления работоспособности объекта отказы различаются на: · устраняемые в эксплуатационных условиях; · устраняемые в стационарных условиях. По внешним проявлениям отказы делятся на явные и скрытые. По взаимосвязям между отказами различают первичные отказы и вторичные (зависимые) отказы. По условиям возникновения различают отказы при хранении, транспортировке, холостом пробеге, при выполнении основной работы. По уровню внешних воздействий различают отказы, возникающие при нормальных и экстремальных условиях эксплуатации. По возможности прогнозирования различают: • прогнозируемые по сроку службы или ресурсу; • прогнозируемые по параметрам объекта; • непрогнозируемые. По характеру возникновения различают постепенные и внезапные отказы. Постепенные отказы возникают в результате возрастающей потери работоспособности элементов объекта. Это обусловливается протеканием процессов старения, износа, коррозии и т.д. Основным признаком постепенного отказа является то, что вероятность его возникновения Q(t) в течение заданного периода времени от t1 до t2 зависит от длительности его предыдущей работы t1. Чем больше эксплуатируется объект, тем выше вероятность возникновения отказа. Внезапные отказы объекта проявляются в виде внезапной полной потери работоспособности. Они возникают в результате сочетания неблагоприятных факторов и случайных воздействий. Отказ возникает через некоторый промежуток времени t1, который является случайной величиной. Основным признаком внезапного отказа является независимость вероятности его возникновения Q(t) в течение заданного периода времени от t1 до t2 от длительности предыдущей работы объекта t1. К таким отказам относятся поломки от чрезмерной нагрузки, усталости, тепловые трещины и др. Отказ происходит внезапно, без предшествующих признаков. По системам и агрегатам машины различают отказы: несущей системы (конструкции); трансмиссии; ходовой части; рабочих органов; электрооборудования; гидросистемы; пневмосистемы; системы управления и т.д. 9.4.2. Причины отказов технических систем
Долговечность любой технической системы характеризуется в основном двумя факторами: • ранними отказами – выходом системы из строя в начале эксплуатации из-за дефектов, выявляющихся в этот период; они уменьшаются по мере приработки • отказами, вызванными длительной эксплуатацией, количество которых возрастает по мере использования технической системы и ухудшения свойств ее деталей. Ранние отказы – это отказы в начальный период работы механической системы могут быть следствием: несовершенства конструкции; погрешностей изготовления; погрешностей монтажа; ошибок, допущенных при вводе в эксплуатацию; неправильной эксплуатации (рис. 9.3). Ошибки конструирования в основном проявляются в течение короткого периода времени, поскольку длительная эксплуатация очень несовершенной конструкции невозможна. Менее значительные дефекты конструкции приводят к большим значениям интенсивности потока отказов в течение длительного промежутка времени.
Рис. 9.3. Интенсивность потока отказов в ранний период эксплуатации машины: 1 - несовершенство конструкция; 2 - погрешности изготовления; 3 - погрешности монтажа; 4 - ошибки при вводе в эксплуатацию; 5 - ошибки эксплуатации
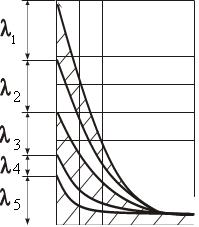
Рис.9.4. Влияние факторов ранних отказов на интенсивность потока отказов в начальный период эксплуатации машины (обозначения см. на рис. 9.3)
Погрешности изготовления носят более случайный характер и проявляются в длительный промежуток времени, который зависит от вида изделия и рода погрешности – дефектный материал, неквалифицированное исполнение, а также от значимости каждой из этих погрешностей. Погрешности монтажа могут включать в себя монтаж не тех деталей, неправильное размещение деталей, отсутствие важных деталей (например, пружинных шайб и т.п.). Ошибки при вводе в эксплуатацию дают малые значения интенсивности потока отказов, но сокращают ресурс машины (например, эксплуатация двигателя в период приработки и т.п.). Недостатки эксплуатации зависят от степени обученности персонала, поэтому ордината l5 снижается в начальный период, а затем остается постоянной. На рис.9.4 показано совокупное влияние всех возможных факторов ранних отказов. Со временем ординаты всех кривых, за исключением связанных со степенью обученности персонала, стремятся к нулю. Отказы в период завершения эксплуатации – этот период эксплуатации характеризуется тем, что система перестает функционировать. Характеристики деталей настолько ухудшаются, что они больше не в состоянии выполнять свои функции, необходимые для обеспечения работы системы. Такие отказы вызываются: разрушением конструкции вследствие перегрузки; ослаблением креплений; уменьшением прочности материала (рис.9.5). Перегрузка может быть вызвана неправильной эксплуатацией машины. Наибольшая вероятность отказа возникает при больших перегрузках машины, даже если и не возникает внезапного отказа.
Рис.9.5. Интенсивность потока отказов в завершающий период эксплуатации машины: 1 – перегрузки; 2 – ослабление креплений; 3 – ухудшение свойств материала
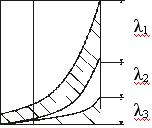
После больших перегрузок могут увеличиваться зазоры и деформации, что вызовет прогрессивное возрастание динамических нагрузок, которые в свою очередь приведут к дальнейшим деформациям, сопровождаемым увеличением динамических нагрузок. Ослабление крепежных деталей, таких как гайки связано с перегрузками. Но ослабление возможно и вследствие усталости в результате фреттинг-коррозии. После некоторого периода эксплуатации все крепления разбалтываются и происходит ослабление крепления. Ухудшение свойств материала происходит непрерывно с момента приложения нагрузок и возникновения взаимодействия кристаллов. Совокупное влияние этих факторов должно вызывать увеличение интенсивности потока отказов (рис. 9.6).
Рис.9.6. Влияние факторов поздних отказов на интенсивность потока отказов в завершающий период эксплуатации машины (обозначения см. на рис.9.5)
9.5. Повышение надежности на стадии разработки конструктивных решений изделия и его составных частей
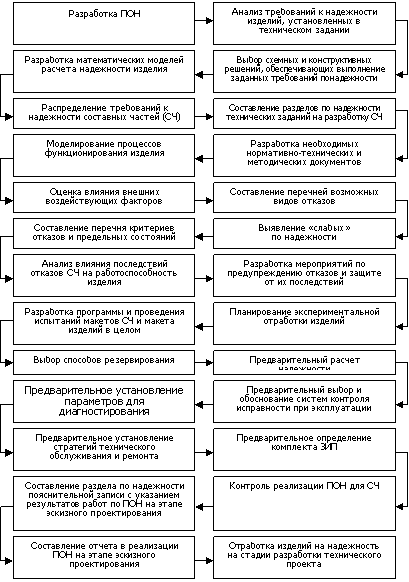
Стадия “Технический проект ”является основным этапом проектирования изделий. На этом этапе должно обеспечиваться и подтверждаться соответствие достигнутого уровня надежности разрабатываемого или модернизируемого изделия нормативным требованиям; на этом же этапе должны быть выявлены все основные “слабые ” элементы конструкции, установлены ожидаемые причины отказов. Проводимые же на этой стадии мероприятия по повышению надежности должны учитывать и быть взаимосвязаны как с технологией изготовления, так и со стратегиями технического обслуживания и ремонта техники. На стадии “Технический проект ”выполняются следующие основные виды работ по обеспечению надежности [25]: - разработка ПОН («Программы обеспечения надежности»); - установление требований к надежности, выбор номенклатуры и нормирование показателей надежности изделий с учетом особенностей его конструктивного исполнения, режимов применения и условий эксплуатации; анализ надежности лучших отечественных и зарубежных аналогов, составных частей, комплектующих изделий, свойств конструкционных материалов; - изучение условий эксплуатации и внешних воздействующих факторов ; - анализ возможных схемно-конструктивных вариантов построения изделия, расчеты надежности этих вариантов изделий и выбор наилучшего по надежности варианта; - выбор конструктивных материалов и комплектующих элементов с учетом требований к надежности; - разработка методов и средств испытаний; - разработка мероприятий, обеспечивающих стойкость изделий к внешним воздействиям; - уточнение оценок показателей надежности изделия в целом его составных частей для выбранного варианта построения изделия; - анализ причин отказов опытных образцов, разработка мероприятий по их устранению; - испытания на надежность макетов опытных образцов изделия и его составных частей; - анализ ремонтной и эксплуатационной документации с точки зрения обеспечения надежности; - разработка системы сбора и обработки информации о надежности изделия и его составных частей на различных стадиях жизненного цикла изделий; - анализ технологии изготовления с точки зрения обеспечения требований к надежности; - технико-экономический анализ эффективности проводимых на стадии НИОКР мероприятий по обеспечению надежности; - разработка нормативно-технической и методической документации, необходимой для обеспечения надежности.
Типовая последовательность проведения мероприятий по отработке изделий на надежность на стадиях разработки аванпроекта и эскизного проекта показана на рис.9.7-9.8.
Рис.9.7. Отработка изделий на надежность на различных стадиях жизненного цикла
В зависимости от вида техники этот состав работ может быть изменен в сторону уточнения, связанных с возможностями и квалификацией работников конструкторских бюро. Как правило, за основу отработки на надежность машин должна приниматься требуемая (назначенная, гарантируемая) наработка Ттр, ресурс или срок службы. В зависимости от величины этой наработки или ресурса конструктор и разработчик выбирают материалы, проводят прочностные расчёты, выбирают конструктивное исполнение изделия, размеры, технологические процессы, системы технического обслуживания и ремонта так, чтобы обеспечить эти нормы для проектируемого объекта.
Рис. 9.8. Этапы отработки изделий на надежность на стадии эскизного проекта
Например. Для машин сезонного использования требуемая наработка равна наработке за агросезон, для гибких производственных систем и автоматических линий – требуемая наработка за сутки или за неделю. По каждому принятому конструктивному решению определяется вероятность, с которой обеспечивается требуемый норматив по безотказности или долговечности, то есть вероятность безотказной работы (ВБР) за требуемую наработку Р(Ттр). Например. Для зерноуборочных комбайнов «Дон» установлено требование, чтобы конструкция, технология и правила эксплуатации обеспечивали работоспособное состояние в течение Ттр = 100 ч. Исходя из этой цифры проводится отработка конструкции комбайна, технологии и системы технического обслуживания. Расчеты же показывают, что эта наработка обеспечивается с вероятностью 0,98. Это значит, что 2% комбайнов не удовлетворяют регламентированным требованиям к безотказности. Уменьшить эту вероятность может быть экономически, нецелесообразно. Для изделий, отказы которых связаны с угрозой безопасности человека, окружающей среде или с большими экономическими потерями, в основу наработки принимается назначенный ресурс. Основными способами и методами обеспечения надежности на данной стадии являются: рациональный выбор конструктивного исполнения изделия; введение резервирования; обоснование запасов прочности, введение в конструкцию средств автоматического обнаружения отказов и определения предотказного состояния средствами технического диагностирования; расчет размерных цепей и обоснование допусков на размеры и параметры; выбор смазок; обеспечение ремонтной и эксплуатационной технологичности, проведение испытаний и расчетов надежности; установление требований к надежности комплектующих изделий; к качеству конструкционных и смазочных материалов. Надежность объекта проектирования может быть повышена также путем: - увеличения числа анализируемых на надежность проектных решений; более детального и всестороннего анализа надежности каждого проектного решения; - повышения точности используемых методов расчета надежности; - автоматизации информационных потоков о надежности между различными подразделениями (данные об аналогах, результаты испытаний макетов, данные о свойствах материалов и т. п.); - -создания и совершенствования методов, позволяющих формализовать проектно-поисковые исследования и объективно делать оценки и прогноз надежности. Отработка изделий на надежность, как правило, сопутствует это изделие на всем жизненном цикле и не ограничивается работами при проектировании (рис. 9.7). 9.6. Повышение надежности систем за счет резервирования
Уровень надежности определяется в процессе проектирования. На последующих этапах изготовления, сборки, эксплуатации изделия, заложенный уровень схемной надежности повысить невозможно. Схемная надежность может быть изменена путем изменения структуры системы, физическая надежность – путем изменения конструкции деталей. Так, например, при последовательном соединении элементов вероятность безоткатной работы (ВБР) системы будет падать с увеличением числа элементов, входящих в эту систему (рис. 9.9). Повышение надежности системы можно добиться с увеличением числа элементов при параллельном их соединении (рис. 9.10).
Рис. 9.9. Зависимость вероятности безотказной работы системы от количества последовательно соединенных элементов: P – вероятность безотказной работы (ВБР) системы ; n – число элементов системы ; цыфры над кривой – ВБР каждого элемента из которых составлена система
Но при этом следует заметить, как в том случае, так и в другом состояние системы во многом определяется ВБР самого элемента, входящего в системы.
Рис. 9.10. Повышение надежности при параллельном соединении m элементов
Способ повышения надежности за счет увеличения параллельных элементов в сельхозмашиностроении не может быть реализован, так как механическую систему с большим числом параллельных элементов трудно спроектировать, да и к тому же, подключение большого числа параллельных элементов дает все меньший эффект. Все же, при необходимости, в технике применяют введение избыточных элементов с целью повышения надежности системы. Такой метод повышения надежности называется резервированием. Резервирование – метод обеспечения надежности, состоящий в применении дополнительных средств и возможностей с целью сохранения работоспособности объекта при отказе одного или нескольких его элементов или нарушении связей между ними. Резервирование целесообразно использовать в тех случаях, когда другие методы повышения надежности оказываются недостаточными или ими нельзя воспользоваться в полной мере из-за ограничений, возникающих при проектировании и эксплуатации систем. Основой резервирования является введение избыточности дополнительных элементов. Резервирование может быть выполнено за счет поэлементного (раздельного) резервирования (рис.9.11) или за счет общего резервирования (рис.9.12). При раздельном резервировании ВБР группы, параллельно соединенных элементов, определяется по выражению Рпар = 1–(1–Рi)m,
а ВБР всех этих последовательно соединенных эквивалентных элементов, т.е. для всей системы, определяется следующим образом:
где n – количество элементов в системе; Рi – ВБР– i-го элемента; m – количество резервных элементов.
Рис.9.11. Поэлементное или раздельное резервирование
Рис.9.12. Общее резервирование
В системе с общим резервированием определяется сначала ВБР каждой из последовательных цепочек, а затем уже самой системы
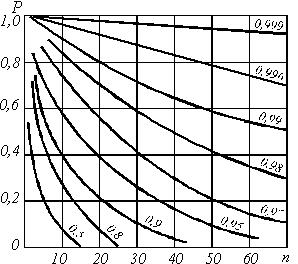
где Pпос – ВБР системы с последовательным соединением элементов (т.е. каждой параллельной ветви); Рсис.о – ВБР системы с общим резервированием. Расчеты показывают, что при различных значениях т и п, надежность при раздельном резервировании всегда выше. Иллюстрацией этого может служить семейство кривых вероятности безотказной работы конкретного изделия Р=j×(n) при различных значениях т (рис. 9.13).Эти кривые дают наглядное представление о том, насколько эффективнее способ раздельного резервирования. Отметим, что постоянное включение резерва (активное резервирование) и включение резерва способом замещения (пассивное резервирование) в общем случае не являются равноценными. Если резервные элементы имеют в процессе дежурства облегченные условия работы, то активное резервирование принципиально более выгодно, чем пассивное, причем преимущество активного резервирования тем заметнее, чем более облегчен дежурный режим резерва. В этом случае выигрыш в надежности благодаря включению способом замещения может быть значителен.
Рис.9.13. Зависимость вероятности безотказной работы системы от n и m при различных способах резервирования
Применение раздельного резервирования совместно с включением резерва способом замещения – наиболее эффективный прием резервирования, позволяющий получить высокую надежность сложного изделия [9].
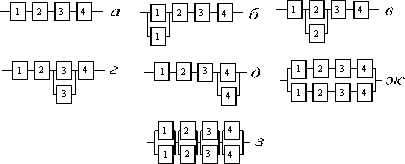
Пример. Найти ВБР системы, состоящей из четырех элементов: ВБР 1-го -0.9, 2-го – 0.8, 3-го – 0.7, 4-го – 0.6 , для случаев: 1) последовательного соединения элементов (рис.9.14, а); 2) резервирования одного из элементов (рис.9.14, б…д); 3) общего резервирования системы (рис.9.14, ж); 4) раздельного резервирования каждого элемента (рис.9.14, з)
Рис.9.14. Варианты соединения элементов в системе
1. ВБР для последовательного соединения (см. рис.9.14, а):
2. Резервирование одного из элементов: 1-го элемента (см. рис.9.14, б)
2-го элемента (см. рис.9.14, в)
3-го элемента (см. рис.9.14, г)
4-го элемента (см. рис. 11.14, д)
3. Общее резервирование (см. рис.9.14, ж)
4. Раздельное резервирование каждого элемента (см. рис.9.14,з)
Из сказанного можно сделать вывод, что надежность машин необходимо рассматривать на самой ранней стадии процесса проектирования, когда внесение изменений в структуру не вызывает серьезных затруднений. При предварительной оценке безотказности системы и выборе способов повышения безотказности рекомендуется учитывать: при последовательном соединении элементов ВБР системы ниже, чем у наименее «надежного элемента («хуже худшего»); при параллельном соединении элементов ВБР системы выше, чем у наиболее надежного элемента («лучше лучшего»);
резервирование системы с последовательным соединением элементов целесообразно начинать с наиболее ненадежных элементов (в этом случае повышение ВБР системы наибольшее (см. пример)); раздельное резервирование каждого элемента повышает ВБР системы больше, чем общее резервирование.
9.7. Достижение заданного уровня надёжности элементов СХМ расчётными методами
Вероятностные методы расчета на усталость элементов конструкции обладают рядом преимуществ перед методами, основанными на детерминистических представлениях (расчеты по запасам прочности, по допускаемым напряжениям и т.п.), поскольку позволяют учитывать изменчивость параметров спектров действующих напряжений и рассеивание характеристик выносливости и дают возможность охарактеризовать их влияние на вероятность разрушения. Необходимо иметь в виду, что некоторые конструктивные и технологические варианты деталей, обладающие высокими показателями прочности по средним значениям, а значит, и наиболее выгодные по сравнению с другими вариантами при обычных методах расчета, могут оказаться менее надежными из-за большого рассеивания характеристик прочности. При вероятностной оценке долговечности элементов конструкции, испытывающих переменные нагрузки, необходимо знать не только средние значения пределов выносливости и долговечности, но и характеристики их рассеивания, в частности, коэффициенты вариации пределов выносливости натурных деталей. Однако проведение испытаний на усталость (в статистическом аспекте) весьма затруднительно из-за потребности большого количества натурных деталей (обеспечение репрезентативности выборки). Кроме того, значительные трудности возникают и при имитации эксплуатационных нагрузок. Поэтому важное значение имеет разработка рациональных методов оценки рассеивания характеристик выносливости натурных деталей по результатам испытаний образцов и моделей [9, 42].
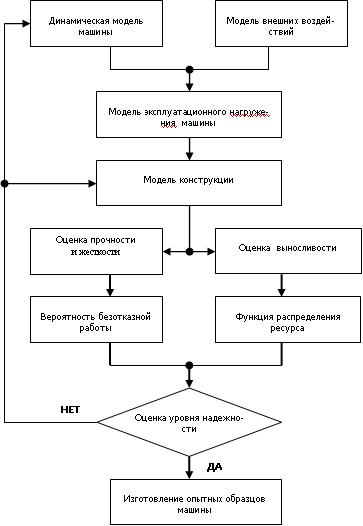
Рассеивание характеристик выносливости натурных деталей серийных и массовых конструкций обусловлено: 1) микроскопическими источниками рассеивания, связанными со структурой неоднородностью металла – размерами, формой и ориентацией зерен, наличием фаз, включений, искажений кристаллической решетки, случайными изменениями в микрогеометрии и структуре поверхностного слоя и т.д.; 2) разбросом механических свойств металла одной марки, но различных плавок, отклонениями в процессе обработки детали, например, в режимах термической обработки при закалке различных партий деталей, а также видов заготовительных операций – ковка, штамповка, прессование и т.п.; 3) отклонениями фактических размеров деталей от номинальных в пределах полей допусков. Особенно существенное влияние на выносливость деталей оказывают погрешности радиусов кривизны в зонах концентрации напряжений – галтели, канавки, и т.д.; 4) технологическими факторами: сваркой, поверхностным упрочнением, покрытием, и т.д.; 5) эксплуатационными факторами: колебаниями температуры, коррозией, появлением поверхностных повреждений в процессе эксплуатации, изменением величины зазора в сочленяемых деталях и т.д. Расчетный прогноз уровня физической надежности наиболее эффективен на ранних стадиях проектирования, до изготовления макетов и опытных образцов машин. Прогноз реализуется на базе информации о внешних воздействиях во всех предполагаемых режимах использования машин, математических моделях эксплуатационной нагруженности машин в целом и каждого рассматриваемого элемента, модели работоспособности детали при возможных характерах их повреждений. Прогнозирование уровня надежности элементов машин расчетными методами может быть осуществлено по схеме, представленной на рис.9.15.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
9.7.6. Оценка уровня надежности
Оценка уровня надежности производится путём сравнения заданного (нормированного) и полученного (прогнозируемого) уровней надежности по ВБР
(вероятности безотказной работы) при заданном ресурсе ТР (наработке). Допускаются отклонения 10…15% в запас. При несоблюдении этого условия
необходимо вернутся в начало блок-схемы (см. рис.9.15) и проделать следующие мероприятия:
провести снижение динамических нагрузок за счет виброзащитных средств, рациональной компоновки основных масс машины и т.п.;
провести конструктивные изменения (геометрии, точности, термической обработки, марки материалов и т.п.) для установления соответствия конструкции воспринимаемым нагрузкам.
9.8. Определение требуемой надёжности
Проблема надежности – самая острая проблема в машиностроении, особенно в сельскохозяйственном машиностроении. Для достижения показателей лучших мировых образцов сельскохозяйственных машин необходимо повысить надежность в 1,8…2,0 раза и при этом снизить материалоемкость на 25…30 %.
Существующее положение обусловлено несоответствием показателей качества сельскохозяйственных машин, определяемых не только современным техническим уровнем, но и данными задания на разработку новой машины, и реальными показателями, достигаемыми в проекте и в серийном производстве. Использование аналоговых методов проектирования, эвристического подхода к принятию решений и эмпирических способов их оценки не гарантирует устанавливаемого техническим заданием уровня надежности и материалоемкости, а предусматривает доработку конструкции в процессе серийного производства машин.
Достижение заданного уровня надежности машин минимальной материалоемкости возможно только при такой методологии проектирования, которая основана на непрерывном прогнозировании показателей надежности на всех стадиях жизненного цикла машины, её идеальной части (проектирование) и материальной части (изготовление и эксплуатация).
Рассмотрим такую методологию проектирования на примере.
Пример. Разработать мероприятия по обеспечению требуемых показателей надёжности вентилятора очистки комбайна Дон-1500.
Наработка на отказ, по данным ГСКБ АО «Ростсельмаш», ![]() часов. Ресурс комбайна
часов. Ресурс комбайна ![]() часов.
часов.
1. Нормирование показателей надёжности.
Нормированию подлежит в первую очередь вероятность безотказной работы ![]() с оценкой ресурса
с оценкой ресурса ![]() . В течение которого она регламентируется. В табл.9.1 представлены классы надёжности изделий.
. В течение которого она регламентируется. В табл.9.1 представлены классы надёжности изделий.
Таблица 9.1
Классы надёжности изделий
|
Класс надёжности |
0 |
1 |
2 |
3 |
4 |
5 |
|
Допустимое значение вероятности безотказной работы |
0,9 |
0,9 |
0,99 |
0,999 |
0,9999 |
1 |
Требования к показателям надежности машины (агрегата) разрабатываются на основе следующих условий:
- учитывая из сложившихся в практике изменений этих показателей в предыдущее время (пассивный прогноз);
- исходя из требований создания машины, не уступающей по своим показателям лучшим мировым образцам;
- исходя из необходимости получения максимального эффекта (минимальных затрат).
2. Расчленение машины на структурные элементы.
Основной задачей разработки требований к надёжности элементов машины является обоснование нормативных значений показателей их надёжности, обеспечивающих требуемые показатели надёжности машины в целом при минимальных затратах.
Первоначальным этапом решения данной задачи является расчленение машины на соответствующие элементы. Следует стремиться разбить машину на части, отказ одной из которых не должен изменять надёжность других, т.е. эти части будут отказывать независимо друг от друга. С другой стороны, учитывая агрегатно-узловой метод ремонта машины, следует расчленить её на части, которые можно ремонтировать независимо друг от друга.
Разбиваем машину на подсистемы, подсистемы - на агрегаты, агрегаты - на узлы, узлы - на сборочные единицы и детали. При этом рассматриваем ту подсистему, в которою входит заданный элемент – вал ротора с подшипниками качения.
Структурная и принципиальная схемы комбайна представлены на рис.9.18, 9.19.
В нашем случае разбивка первого уровня: 1- жатвенная часть; 2 – ходовая часть; 3 – кабина; 4 – молотильная группа; 5 – моторная установка; 6 – копнитель (см. рис.9.18).
Заданный элемент – вал вентилятора – входит в подсистему «Молотильная группа». Поэтому разбивка второго уровня производится только указанной подсистемы: обмолачивающая часть (4.1), очистка (4.2).
Третий уровень: четыре сборочные единицы, среди которых вентилятор имеет индекс 4.2.2 (см. рис.9.19).
Вычленение вала как детали происходит только на четвёртом уровне разбивки и при этом ему присваивается индекс 4.2.2.3.6.
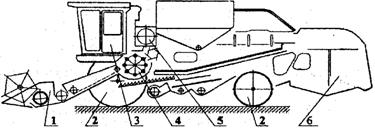
Рис. 9.18. Принципиальная схема комбайна
3. Определение требуемых показателей надёжности.
Как показала практика, для большинства агрегатов на значительном интервале времени поток отказов с достаточной для практических расчётов точностью можно считать как стационарный пуассоновский поток с параметром ![]() , равным среднему значению параметра потоков отказов. Поскольку отказ каждого отдельного агрегата не зависит от отказов других, то для системы, изображённой на рис.9.19, можно написать:
, равным среднему значению параметра потоков отказов. Поскольку отказ каждого отдельного агрегата не зависит от отказов других, то для системы, изображённой на рис.9.19, можно написать:
![]() ,
,
где ![]() интенсивность отказов всей системы;
интенсивность отказов всей системы; ![]() интенсивность отказов
интенсивность отказов ![]() -того агрегата.
-того агрегата.
Это выражение может быть преобразовано следующим образом:
![]() ,
,
где ![]() коэффициенты весомости, зависящие от сложности агрегата, его стоимости и других факторов.
коэффициенты весомости, зависящие от сложности агрегата, его стоимости и других факторов.
Этот коэффициент может быть найден расчётным или экспертным путём.
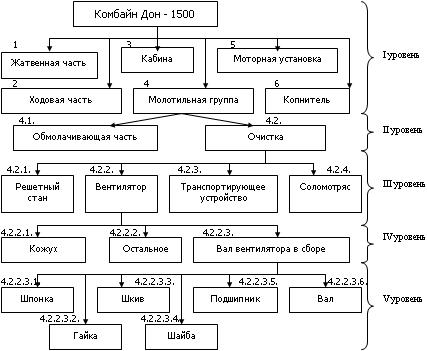
Рис.9.19. Структурная схема комбайна Дон-1500
3.1. Расчёт весовых множителей.
В основу методики определения весовых множителей положены следующие допущения:
- стоимость структурной единицы машины отражает уровень конструкторских и технологических решений и достигнутого уровня надёжности в условиях данного производства;
- чем сложнее структурная единица, чем выше трудоёмкость её изготовления, тем она дороже и тем менее желателен её отказ;
- чем выше трудоёмкость монтажа и демонтажа агрегата (элемента) на машину, тем менее желателен её отказ этого агрегата (элемента);
- интенсивность отказов постоянна за весь жизненный цикл агрегата, узла, сборочной единицы, детали.
Принимая такие допущения, можно предложить следующий порядок расчёта весовых множителей.
3.1.1. Определить интенсивность отказов всей системы (машины)
![]() ,
,
где ![]() требуемая средняя наработка на отказ.
требуемая средняя наработка на отказ.
![]() отказ/час.
отказ/час.
3.1.2. Определение весовых множителей для структурных единиц высшего уровня:
 ,
,
где ![]() стоимость
стоимость ![]() -й системы;
-й системы; ![]() трудоёмкость монтажа
трудоёмкость монтажа ![]() -й системы на машину;
-й системы на машину; ![]() число систем.
число систем.
Контрольным условием является ![]() . Тогда требуемые интенсивности отказов системы будут определяться по выражению
. Тогда требуемые интенсивности отказов системы будут определяться по выражению
![]() .
.
Контрольное условие ![]() .
.
3.1.3. Определение весовых множителей для структурных единиц нижнего порядка.
Весовые множители для подсистем, узлов, сборочных единиц и деталей определяются по приведённому выше выражению, только значение ![]() принимается по числу сборочных единиц или по числу деталей. При этом контрольное условие в каждой подсистеме сохраняется
принимается по числу сборочных единиц или по числу деталей. При этом контрольное условие в каждой подсистеме сохраняется ![]() ;
;
![]() ;
; ![]() ;
; ![]() ,
,
где ![]() интенсивность отказов
интенсивность отказов ![]() -й подсистемы;
-й подсистемы; ![]() интенсивность отказов
интенсивность отказов ![]() -го узла;
-го узла; ![]() интенсивность отказов
интенсивность отказов ![]() -й сборочной единицы.
-й сборочной единицы.
3.2. Определение весовых множителей экспертным путём
В случае, когда нет данных по трудоёмкости монтажа и стоимости элементов машины, весовые множители можно определить экспертным путём по аналогии с известным опытом. Одним из видов экспертного определения коэффициента ![]() является применение разновидности метода баллов. При этом последовательно каждый агрегат сопоставляется с другими агрегатами системы. Если рассматриваемый агрегат стоит меньше сравниваемого, то ему присваивают 0 баллов, а если больше – 1 балл.
является применение разновидности метода баллов. При этом последовательно каждый агрегат сопоставляется с другими агрегатами системы. Если рассматриваемый агрегат стоит меньше сравниваемого, то ему присваивают 0 баллов, а если больше – 1 балл.
Определим весовые множители для структур первого уровня (табл.9.2).
Таблица 9.2
Расчёт весовых множителей (см. рис.9.18)
|
Номер блока |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
|
|
1 |
- |
1 |
1 |
0 |
0 |
0 |
2 |
0.13 |
0.13 |
0.085×10-3 |
|
2 |
0 |
- |
0 |
0 |
0 |
0 |
0 |
0 |
0.05 |
0.033×10-3 |
|
3 |
0 |
1 |
- |
0 |
0 |
0 |
1 |
0.07 |
0.07 |
0.056×10-3 |
|
4 |
1 |
1 |
1 |
- |
0 |
1 |
4 |
0.25 |
0.25 |
0.170×10-3 |
|
5 |
1 |
1 |
1 |
1 |
- |
1 |
5 |
0.33 |
0.3 |
0.200×10-3 |
|
6 |
1 |
1 |
1 |
0 |
0 |
- |
3 |
0.2 |
0.2 |
0.132×10-3 |
|
Итого: |
15 |
- |
1 |
6.600×10-3 |
||||||
Примечание: поскольку ![]() не может быть равным нулю, то принимаем
не может быть равным нулю, то принимаем ![]() , но
, но ![]() , поэтому уменьшаем значение старших значений, чтобы выдержать это соотношение.
, поэтому уменьшаем значение старших значений, чтобы выдержать это соотношение.
Второй уровень содержит два блока. По нашему мнению, очистка более трудоемка в изготовлении, а следовательно, и по стоимости. Поэтому принимаем:
![]() ;
; ![]() ;
; ![]()
![]() .
.
Третий уровень содержит четыре приблизительно одинаковых и по стоимости, и по трудоёмкости блоков. Можно предположить, что весовые множители их равны, то есть:
![]() .
.
Аналогично предыдущему уровню определяем весовые множители четвертого уровня:
![]() ;
;
![]() Для пятого уровня можно исключить такие детали, как гайка, шайба, шпонка - как не имеющие износ за время работы. Остальные три детали примем равными по стоимости и трудоёмкости.
Для пятого уровня можно исключить такие детали, как гайка, шайба, шпонка - как не имеющие износ за время работы. Остальные три детали примем равными по стоимости и трудоёмкости.
Тогда:
![]() ;
;
![]()
3.3. Распределение наработки на отказ между элементами.
Для ординарных потоков отказов элементов системы отказы элементов совпадают с параметрами потока. В связи с тем, что интенсивность потока отказов каждого элемента стремится к пределам
![]() ,
,
то интенсивность потока отказов системы
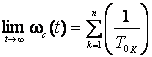 ,
,
где ![]() нормальные наработки на отказ.
нормальные наработки на отказ.
Исходя из этого можно ориентировочно записать
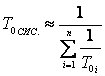 ,
,
или
![]() .
.
Эти зависимости являются точными на любом участке времени и при любом числе элементов лишь при экспоненциальном законе распределения наработки на отказ каждого агрегата. Для других законов эта зависимость является приближённой. При указанных допущениях по аналогии могут быть определены требования к средней наработке на отказ каждого элемента машины.
Элементы первого уровня определим по табл.9.3.
Таблица 9.3
Распределение наработки на отказ между элементами первого уровня
|
Номер системы |
1 |
2 |
3 |
4 |
5 |
6 |
|
Весовой множитель системы |
0,13 |
0,05 |
0,07 |
0,25 |
0,5 |
0,2 |
|
Наработка на отказ блока системы, ч |
1154 |
3000 |
2143 |
600 |
300 |
750 |
Элементы второго уровня:
![]() часов;
часов;
![]() часов;
часов;
Элементы третьего уровня. Поскольку весовые коэффициенты элементов этого уровня равны между собой, то наработка на отказ для всех элементов будет одинаковой:
![]() часов.
часов.
Согласно передовому опыту машиностроения, наработка на отказ механизмов аналогичного типа находится в пределах 4000…5000 маш. ч [1]. Расчетное значение наработки на отказ для вентилятора очистки равно 4000 часов, которое не превышает достигнутого уровня. Исходя из этого принимаем ![]() часов.
часов.
3.4. Распределение вероятности безотказной работы.
При сделанных выше допущениях вероятность безотказной работы системы (машины) можно считать равной
![]() ,
,
где ![]() основание натурального логарифма;
основание натурального логарифма; ![]() наработка на отказ
наработка на отказ ![]() -го блока системы.
-го блока системы.
Если в блоке системы имеются несколько одинаковых деталей, то вероятность безотказной работы каждой определяется по выражению
![]() ,
,
где ![]() количество одинаковых деталей в блоке.
количество одинаковых деталей в блоке.
Исходя из требований задания определим вероятность безотказной работы деталей пятого уровня из условия обеспечения наработки на отказ блока вентилятора очистки ![]() часов:
часов:
вал вентилятора очистки:
![]() ;
;
подшипник вентилятора очистки:
![]() ,
,
где ![]() , так как на валу стоят два одинаковых подшипника.
, так как на валу стоят два одинаковых подшипника.
4. Установление достигнутого уровня надежности при конструировании элементов машин.
Фактически достигнутый уровень надежности может быть установлен одним из следующих способов:
· проведение ресурсных испытаний, в результате которых могут быть получены физические отказы элементов машин;
· экспериментальная оценка эксплуатационной машины и её элементов, прогнозирование на базе этих данных достигнутого уровня надежности;
· расчетная оценка экспериментальной нагруженности машины и её элементов, прогнозирование на базе расчётов достигнутого уровня надёжности.
4.1. Прогнозирование уровня надежности деталей машины расчетными методами.
Расчетный прогноз уровня надежности наиболее эффективен на ранних стадиях проектирования, так как не требует изготовления опытного образца машины или её части, а также не требует проведения экспериментальных исследований.
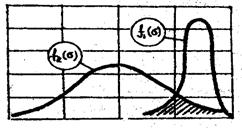
Процесс эксплуатационного нагружения деталей сельскохозяйственных машин носит, как правило, случайный характер и должен описываться вспомогательными характеристиками. При отсутствии возможности получить такие характеристики, в первом приближении можно рассчитывать параметры случайного распределения из условия его подчинения нормальному закону (рис.9.20).
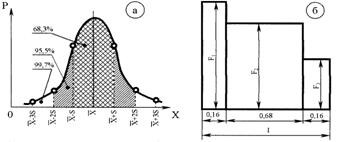
Рис.9.20. Функция нормального распределения (а) и график нагруженности,
отрабатывающий эту функцию (б)
При этом необходимо знать минимальное значение ![]() и максимальное значение
и максимальное значение ![]() процесса. Тогда математическое ожидание процесса можно определить по выражению
процесса. Тогда математическое ожидание процесса можно определить по выражению
![]() ;
;
среднее квадратическое отклонение процесса
![]() ;
;
коэффициент вариации
![]() .
.
При разбиении графика функции на три зоны с шагом квантования равным S площадь, ограничиваемая этими точками, будет равна:
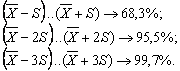
Исходя из этого величины блоков для графика нагруженности определяются из выражений:
![]()
![]()
![]()
4.1.1. Расчет функции долговечности валов и осей.
Расчет функции долговечности необходимо вести для всех сечений, имеющих концентраторы напряжений с целью оптимизации конструкции по металлоемкости.
Для расчета ресурса следует определить напряжения в сечении при действии гистограммы нагрузок:
от действия изгибающего момента
![]() ,
,
где ![]() изгибающие моменты, действующие в расчетном сечении вала согласно отрабатываемой гистограмме нагрузок;
изгибающие моменты, действующие в расчетном сечении вала согласно отрабатываемой гистограмме нагрузок; ![]() – момент сопротивления
– момент сопротивления
для круглого сечения; ![]() – для вала со шпонкой;
– для вала со шпонкой; ![]() – для вала с прямобочными шлицами;
– для вала с прямобочными шлицами;
от действия крутящего момента
![]() ,
,
где ![]() – крутящие моменты, действующие в расчетном сечении вала согласно отрабатываемой гистограмме нагрузок;
– крутящие моменты, действующие в расчетном сечении вала согласно отрабатываемой гистограмме нагрузок; ![]() – полярный момент сопротивления для круглого сечения;
– полярный момент сопротивления для круглого сечения; ![]() – для вала со шпонкой;
– для вала со шпонкой; ![]() – для вала с прямобочными шлицами.
– для вала с прямобочными шлицами.
4.1.2. Проведём расчет характеристик сопротивления усталости при многоцикловом нагружении.
Величины пределов выносливости в опасных сечениях определяются в соответствии с ГОСТ 25.504–82:
![]() ;
; ![]() ,
,
где ![]() медианные значения пределов выносливости материала, определённые на лабораторных образцах;
медианные значения пределов выносливости материала, определённые на лабораторных образцах; ![]() коэффициент, учитывающий снижение механических свойств с ростом размеров заготовок.
коэффициент, учитывающий снижение механических свойств с ростом размеров заготовок.
![]() для
для ![]() мм;
мм;
![]() для
для ![]() мм;
мм;
![]() коэффициент снижения предела выносливости,
коэффициент снижения предела выносливости,
![]() ;
; ![]() ,
,
![]() коэффициенты концентрации напряжений при изгибе и при кручении ;
коэффициенты концентрации напряжений при изгибе и при кручении ; ![]() коэффициенты влияния абсолютных размеров поперечного сечения. С достаточной для инженерных расчётов точностью можно принять
коэффициенты влияния абсолютных размеров поперечного сечения. С достаточной для инженерных расчётов точностью можно принять ![]() ;
; ![]() ;
; ![]() коэффициенты влияния качества обработки поверхности.
коэффициенты влияния качества обработки поверхности.
![]() при
при ![]() мкм;
мкм;
![]() при
при ![]() мкм;
мкм;
![]() ;
;
![]() предел прочности;
предел прочности; ![]() шероховатость поверхности:
шероховатость поверхности: ![]() мкм – грубое точение;
мкм – грубое точение; ![]() мкм – тонкое точение;
мкм – тонкое точение; ![]() мкм – шлифование;
мкм – шлифование; ![]() коэффициент влияния технологических методов поверхностного упрочнения. При отсутствии термообработки
коэффициент влияния технологических методов поверхностного упрочнения. При отсутствии термообработки ![]() .
.
4.1.3. Определение среднего ресурса детали в циклах.
![]() ; ,
; , ![]() ,
,
где- ΝG –абсцисса точки перелома кривой усталости (базовое число циклов), ![]() средний ресурс детали в циклах при действии только нормальных или только касательных напряжений;
средний ресурс детали в циклах при действии только нормальных или только касательных напряжений; ![]() величина, характеризующая условия накопления усталостного повреждения. Можно принять
величина, характеризующая условия накопления усталостного повреждения. Можно принять ![]() . Для более точного определения воспользуемся выражениями:
. Для более точного определения воспользуемся выражениями:
![]() при
при ![]() ;
;
![]() при
при ![]() .
.
![]() ;
;
![]() ;
;
![]() показатель наклона кривой выносливости;
показатель наклона кривой выносливости;
![]() ;
;
![]() коэффициент снижения предела выносливости;
коэффициент снижения предела выносливости; ![]() базовое число циклов;
базовое число циклов;
![]()
при ![]() ;
;
![]()
при ![]() .
.
Для сечений валов, нагруженных изгибающими или крутящими моментами, необходимый ресурс детали проводится либо по изгибающим, либо по крутящим моментам.
Для сечений валов, нагруженных изгибающим и крутящим моментами, расчёт проводится раздельно по каждому из факторов, а эквивалент ресурса определяется по выражению
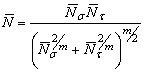 ,
,
где ![]() .
.
4.1.4. Определение среднего ресурса в часах.
![]() ,
,
где ![]() частота приложения нагрузки к детали, мин – 1. Для вращающихся деталей эта частота вращения вала в об/мин.
частота приложения нагрузки к детали, мин – 1. Для вращающихся деталей эта частота вращения вала в об/мин.
Поскольку накопление усталостных повреждений происходит только при условии ![]() , то необходимо исключить те блоки нагружения, напряжения от действия которых меньше
, то необходимо исключить те блоки нагружения, напряжения от действия которых меньше ![]() .
.
При этом
![]() .
.
4.1.5. Определение функции распределения ресурса.
![]() ,
,
где ![]() среднее квадратическое отклонение значения логарифма долговечности;
среднее квадратическое отклонение значения логарифма долговечности; ![]() коэффициенты вариации предела выносливости и приведённых амплитуд.
коэффициенты вариации предела выносливости и приведённых амплитуд. ![]() (рекомендуется принимать
(рекомендуется принимать ![]() ;
; ![]() квантиль нормального распределения.
квантиль нормального распределения.
Поскольку функция распределения ресурса в логарифмических координатах изображается прямой линией , то её можно построить по двум точкам: ![]() (50-процентная вероятность) и по
(50-процентная вероятность) и по ![]() (98-процентная вероятность). Тогда
(98-процентная вероятность). Тогда ![]() .
.
5. Расчёт сечения вала.
Подробно проведём расчёт ресурса для одного сечения.
Пример. Определить ресурс в опасном сечении вала. Вал представляет из себя трубу, на которой приварено кольцо. Опасное сечение содержит концентратор напряжений - сварной шов. В этом сечении действует изгибающий момент ![]() Н×м и крутящий момент
Н×м и крутящий момент ![]() Н×м. Размеры сечения:
Н×м. Размеры сечения: ![]() мм,
мм, ![]() мм.
мм.
В качестве концентратора напряжений в реальной конструкции нашего примера имеется сварное соединение. В этом сечении действует изгибающий момент ![]() Н×м и крутящий момент
Н×м и крутящий момент ![]() Н×м.
Н×м.
Считаем, что нагруженность вала подчиняется нормальному закону, поэтому параметры процесса определим по п. 4.1.
Для изгибающего момента:
![]() Н×мм;
Н×мм;
![]() ;
;
![]() Н×мм;
Н×мм;
![]() Н×мм;
Н×мм;
![]() коэффициент вариации;
коэффициент вариации;
![]() Н×мм - величина нагрузки первого блока гистограммы;
Н×мм - величина нагрузки первого блока гистограммы;
![]() Н×мм - величина нагрузки второго блока гистограммы;
Н×мм - величина нагрузки второго блока гистограммы;
![]() Н×мм - величина нагрузки третьего блока гистограммы.
Н×мм - величина нагрузки третьего блока гистограммы.
Определим нормальные напряжения при действии гистограммы нагрузок.
Момент сопротивления для тонкостенной трубы
![]() мм3 ,
мм3 ,
где ![]() мм – наружный диаметр трубы;
мм – наружный диаметр трубы; ![]() мм – внутренний диаметр трубы;
мм – внутренний диаметр трубы; ![]() мм - толщина стенки трубы.
мм - толщина стенки трубы.
Тогда нормальные напряжения:
![]() МПа;
МПа;
![]() МПа;
МПа;
![]() МПа.
МПа.
Исходя из рекомендаций для сварных конструкций элементов сельскохозяйственных машин, предел выносливости детали будет находится в пределах ![]() МПа.
МПа.
Поскольку накопление усталостных повреждений происходит только при ![]() (
(![]() МПа), то, сравнивая это значение с напряжениями, действующими в этом сечении, можно сделать вывод: накопления усталостных повреждений в этом сечении не будет, и поэтому ресурс бесконечен.
МПа), то, сравнивая это значение с напряжениями, действующими в этом сечении, можно сделать вывод: накопления усталостных повреждений в этом сечении не будет, и поэтому ресурс бесконечен.
Для крутящего момента
![]() Н×мм;
Н×мм;
![]() ;
;
![]() Н×мм;
Н×мм;
![]() Н×мм;
Н×мм;
![]() коэффициент вариации;
коэффициент вариации;
![]() Н×мм - величина нагрузки первого блока гистограммы;
Н×мм - величина нагрузки первого блока гистограммы;
![]() Н×мм - величина нагрузки второго блока гистограммы;
Н×мм - величина нагрузки второго блока гистограммы;
![]() Н×мм - величина нагрузки третьего блока гистограммы.
Н×мм - величина нагрузки третьего блока гистограммы.
Определим касательные напряжения при действии гистограммы нагрузок:
![]() мм3 – момент сопротивления при кручении.
мм3 – момент сопротивления при кручении.
Тогда касательные напряжения
![]() МПа;
МПа;
![]() МПа;
МПа;
![]() МПа.
МПа.
Определим предел выносливости материала детали
![]() МПа;
МПа;
![]() ;
;
![]() ;
;
![]() МПа;
МПа;
![]() МПа,
МПа,
следовательно, накопления усталостных напряжений не будет, и ресурс бесконечен.
Определим средний ресурс детали в циклах при действии только нормальных и касательных напряжений
![]() .
.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Определим эквивалент ресурса детали циклах:
![]() ;
; ![]() .
.
Определим средний ресурс в часах:
![]() ;
; ![]() ч.
ч.
Определим функцию распределения ресурса
![]()
![]() ;
;
Тогда ![]() часов.
часов.
Для построения графика функции ресурса для 98% удобнее принять, что ![]() , т.е.
, т.е.
![]() .
.
6. Расчёт функции долговечности несущих конструкций.
Уровень напряжённого состояния в элементах несущих конструкций определяется по одной из программных
реализаций на ЭВМ, которые используют метод конечного элемента. При раздельном получении напряжений, нормальных и касательных, расчёт функции
долговечности необходимо вести по ![]() . Методика расчёта не отличается от приведённой выше, расчёт функции долговечности необходимо вести по
. Методика расчёта не отличается от приведённой выше, расчёт функции долговечности необходимо вести по ![]() .
.
Для сечений конструкций, не имеющих концентраторов в виде сварных швов, рекомендуется предел выносливости определяется по выражению
![]() ,
,
где ![]() табличная величина предела выносливости;
табличная величина предела выносливости; ![]() ориентировочное значение коэффициента
ориентировочное значение коэффициента
концентрации; ![]() ориентировочное значение коэффициента запаса прочности.
ориентировочное значение коэффициента запаса прочности.
Для сварных конструкций необходимо ![]() назначать по результатам проведенных испытаний. Так, например, на основании проведённых многолетних испытаний ДГТУ рекомендуется для штампосварных конструкций несущих элементов сельскохозяйственных машин назначать предел выносливости детали
назначать по результатам проведенных испытаний. Так, например, на основании проведённых многолетних испытаний ДГТУ рекомендуется для штампосварных конструкций несущих элементов сельскохозяйственных машин назначать предел выносливости детали ![]() МПа.
МПа. ![]() ч. Построим график функции ресурса при вероятности неразрушения 98% (см. пример на рис.9.36 и 9.37).
ч. Построим график функции ресурса при вероятности неразрушения 98% (см. пример на рис.9.36 и 9.37).
9.9. Прогнозирование уровня надёжности элементов машин экспериментально-расчётными методами
Экспериментально-расчетный прогноз уровня физической надеж-ности наиболее эффективен на стадиях
изготовления опытных образцов машины.Исследованиям подвергается не только готовая конструкция,но и ее
образец, в который закладывается технология производства с ее дефектами изготовления и сборки,свойственными для данного производства, то есть отражается культура производства. Общая схема проведения прогноза
представлена на рис. 9.21.Как видно из рисунка, прогноз реализован расчетными методами, но данные для
расчетов получены экспериментальным путем. База экспериментальныхисследований содержит данные
эксплуатационной нагруженности деталей (силовые факторы, напряженно-деформируемое состояние),
полученные, как правило, электротензометрированием , и характеристики предельных состояний деталей
(sТ; s-1q; и др.).Положительным моментом такого прогноза является его относительно высокая точность
оценок – погрешность по долговечности, как правило, не превышает 15…20%, отрицательным моментом –
необходимость изготовления экспериментального образца машины, что отражается на сроках ввода в серийное
производство машины и стоимости проведения такого рода прогноза.
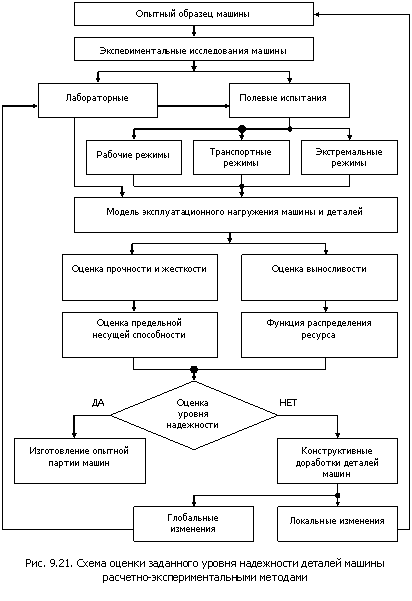
9.9.1. Экспериментальные исследования машины во всех типичных режимах
работы
На основе оценки загруженности машины по режимам эксплуатации с помощью информационно-измерительных
систем (ИИС) проводят исследования эксплуатационной нагруженности машины в целом и отдельных ее
деталей во всех типичных режимах работы.Эксплуатационная нагруженность характеризуется совокупностью статистических показателей процессов, происходящих в машине, ее системах, агрегатах сборочных единицах и деталях в условиях рядовой эксплуатации и
типичных перегрузках во всех природно-климатических зонах, для которых машина предназначена [30, 39].
Доля типового режима в общем объеме эксплуатации парка машин
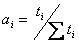 ;
;  ,
,
где ti – суммарное время эксплуатации машины в i-м режиме.
9.9.2. Эксплуатационное нагружение машины и деталей
Эксплуатационные нагрузки вызывают в деталях случайные напряжения. Спектральные плотности случайных
процессов, характеризующих
напряженно-деформированное состояние (НДС) конструкции, являются не только комплексной характеристикой самой системы и действующих
нагрузок, но и исходной информацией для прогнозирования
долговечности. При записях процессов, характеризующих эксплуатационную нагруженность машины,
фиксируются внешние воздействия.
Формирование нагрузок основывается на статистическом материале экспериментальных исследований
образцов машины. Достоверность статистических
оценок зависит от продолжительности наблюдения (записи) процессов. Обработка записей аналоговых сигнало
датчиков (тензоэлементов)проводится в зависимости от цели дальнейших исследований: для оценки прочности
и жесткости (экспериментальное нагружение) или для оценки выносливости (случайный эксплуатационный
процесс нагружений). Для оценки НДС конструкции в экстремальных условиях рассматривается нагружение
в единый момент времени. Для этого на синхронизированных записях определяют величины напряжений или
деформаций, изменяющихся во временив наиболее неблагоприятных сочетаниях. Оценивают вероятность
возникновения перегрузок в данном режиме эксплуатации.
9.9.3. Оценка выносливости
Оценка выносливости базируется на корректированной линейной гипотезе суммирования усталостных
повреждений Серенсена-Когаева [11, 33].При исследовании выносливости конструкций, изготовленных и
сталей малой и средней прочности (sb < 1300 МПа) без воздействий агрессивной среды и при нормальной
температуре, медианные кривые усталости (соответствующие P = 50% неразрушения) имеют горизонтальные
участки, соответствующиенеограниченным пределам выносливости:
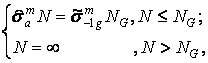
где ![]() – среднее значение амплитуд напряжений; m – показатель угла наклона левой ветви кривой
– среднее значение амплитуд напряжений; m – показатель угла наклона левой ветви кривой
усталости; N – число циклов амплитуд;![]() – медианное значение предела выносливости натурной
– медианное значение предела выносливости натурной
детали; NG – абсцисса точки переломакривой усталости.Поскольку нагруженность представляется
в виде гистограммы , то медианная долговечность для этого ступенчатого распределения амплитуд
напряжений определяется по выражению
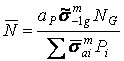 , при sai > s-1g,
, при sai > s-1g,
где аР – расчетная сумма относительных долговечностей; ![]() – случайные и средние значения
– случайные и средние значения
амплитуды напряжений i -й степени;рi – относительное число повторений амплитуды.
Расчетная сумма относительных долговечностей
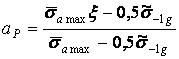 .
.
Корректировочная функция
![]() ,
,
где ![]() ; r – порядковый номер амплитуды, при которой
; r – порядковый номер амплитуды, при которой ![]() и
и ![]() .
.
Медианная долговечность для непрерывного распределения амплитуд напряжений
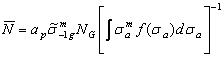 .
.
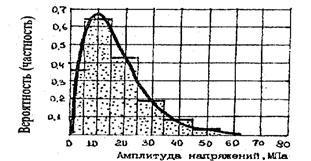
Рис.9.22. Обобщённая гистограмма и теоретический закон распределения эквивалентных
амплитуд напряжений (несущая система Дон-1500)
Значения параметров кривых усталости и их коэффициента вариации определяются экспериментально или
расчетом.Двумерное распределение амплитуд напряжений sа и средних (статических) значений
sm может быть сведено к одномерному распределениюэквивалентных амплтуд
sэкв= sа + yssm ,
где ys – коэффициент чувствительности материала к асимметрии нагружений, для малоуглеродистых
сталей ys » 0,2.В качестве примера на рис. 9.22 показан вид гистограммы и теоретического закона
распределения эквивалентных амплитуд напряжений в несущейконструкции мобильного энергетического модуля.
Средний ресурс в часах работы
![]() ,
,
где nэф – эффективная частота амплитуд повреждающих напряжений (определяется как частота
появления эквивалентных амплитуд напряжений![]() ), Гц.
), Гц.
Функция распределения ресурса может в быть определена в предположении, что подчиняется нормально-логарифмическому закону (см.п.9.7.5.)
9.10. Экспериментальная оценка уровня надёжности машин
9.10.1. Общие положения и классификация
Для создания конкурентоспособных и надежных машин необходимо проводить всестороннюю оценку деталей, сборочных единиц и машины в целом как на стадии изготовления опытных образцов, так и на стадии серийного изготовления [25, 39].
Испытания классифицируются по следующим признакам:
· по целям: 1) производственные: предварительные; приемочные; периодические; 2) исследовательские испытания: аттестационные; граничные;
· по срокам проведения: ускоренные; неускоренные;
· по методу проведения: разрушающие; неразрушающие;
· по этапам: на этапе производства; эксплуатационные.
Контрольные испытания проводятся для контроля качества продукции.
Предварительные испытания опытных образцов или опытных партий проводятся заводом–изготовителем для решения вопроса о возможности предъявления продукции на государственные, межведомственные или ведомственные испытания.
Приёмочные испытания опытных образцов или опытных партий проводятся для решения вопроса о целесообразности производства и передачи их в эксплуатацию (государственный сектор). Обычно эти испытания проводятся комиссией, назначаемой заказчиком.
Периодические испытания – это контрольные испытания готовой продукции, проводимые периодически в объемах и сроки, установленной нормативно-технической документацией (НТД).
Особое место в общей оценке машин занимают испытания на надежность, которые подразделяются: определительные (надежность опытных образцов); контрольные (надежность серийных образцов); ресурсные; ускоренные.
Для проведения испытаний разрабатываются программы, которые могут содержать многоцелевую направленность и включать вопросы как производственного характера, так и научного.
Предусматриваются следующие основные планы проведения наблюдений:
план [N, U, N] – под наблюдение поставлено N изделий, наблюдения ведутся до отказа всех изделий или до предельного состояния, отказывающие детали не заменяются новыми;
план [N, U, T] – под наблюдение поставлено N изделий, наблюдения ведутся до установленной наработки, отказавшие детали не заменяются новыми;
план [N, U, r] – под наблюдение поставлено N изделий, наблюдения ведутся до отказа r изделий или их предельных состояний, отказавшие детали не заменяются новыми;
план [N, R, T] – под наблюдение поставлено N изделий, наблюдения ведутся до установленной наработки T, отказавшие детали заменяются новыми или ремонтируются;
план [N, R, r] – под наблюдение поставлено N изделий, наблюдения ведутся до отказа r изделий или их предельных состояний, отказавшие отдельные детали заменяются новыми или ремонтируются.
План испытаний выбирается головной организацией в зависимости от вида изделия, условий эксплуатации и технической необходимости.
При проведении испытаний на надежность проверяются количественные показатели надежности и сравниваются с теми, которые были приняты на стадии проектирования. Выявляются характерные отказы элементов и узлов, возникающие в машине, и устанавливаются причины их возникновения. По характерным отказам выявляются наиболее слабые места в машине и разрабатываются мероприятия по их устранению.
9.10.2. Состояние проблемы надежности
тракторов и сельхозмашин
Сельхозмашины работают в абразивной среде [37], поэтому основным критерием их работоспособности является износостойкость. Ударные нагрузки от твердых включений в почве делают необходимым встраивание в рабочие органы машин предохранительных муфт или использование передач, обладающих предохраняющей способностью от перегрузок (например, ременных). Ресурс тракторов нормируют не в километрах пробега, как автомобилей, а в часах, что, в частности, связано с сезонностью их работы и хранением под открытым небом, при котором потеря работоспособности из-за коррозии пропорциональна времени. Коррозионное поражение незащищенных поверхностей стальных деталей в атмосферных условия достигает при хранении на открытой площадке 0,44 мм/год против 0,03 мм/год при хранении в закрытом помещении. Для тракторов и зерноуборочных комбайнов сложилась практика нормирования и оценки ресурса агрегатов по 80%-ному гамма-ресурсу. Его обычно назначают кратным времени работы машины в течение нескольких сезонов.
Нагруженность рам сельскохозяйственных машин в значительной степени определяется вертикальными динамическими нагрузками от неровностей дороги и полей. При движении по улучшенным дорогам преобладают симметричные изгибающие нагрузки. При движении по проселочным дорогам и бездорожью преобладают кососимметричные нагрузки, скручивающие раму.
Нагрузки по времени распределены по законам, близким к нормальным. Большие нагрузки характерны для зимней эксплуатации на поле с бороздами (коэффициент динамичности доходит до 2,7).
При расчете трансмиссий тракторов на выносливость за расчетный момент берут меньший из двух: 1) развиваемый двигателем в номинальном режиме работы с учетом передаточного числа передачи; 2) реализуемый при заданном сцепном весе трактора, причем коэффициент сцепления с грунтом для гусеничных тракторов принимают 1,0, а для колесных – 0,7.
Время эксплуатации зубчатых пар коробки перемены передач при ресурсе трансмиссии 8000 ч принимают: для рабочих передач – от 1500 до 3000 ч, для понижающих передач – от 200 до 1000 ч. Агрегаты, расположенные за коробкой передач, рассчитывают на переменный режим работы с временем работы на рабочих передачах 5000…6000 ч и на транспортных и понижающих передачах – 1000…2000 ч. Агрегаты вала отбора мощности рассчитывают на ресурс 8000 ч при передаче полной мощности.
При работе колесного трактора класса 15 кН (при скорости движения 7,5…13 км/ч) замерены следующие колебания тяговой нагрузки: на пахоте стерни – 2500…3000 Н с частотой колебаний 5,8…11,2 Гц ; на пахоте целины — 2600…4000 Н при частоте колебаний 7,3…13 Гц. Пахота отличается наибольшими амплитудами и частотами колебаний нагрузки.
Распределение отказов по узлам для гусеничного трактора характеризовалось следующими цифрами, %: отказы двигателя (поломка шатунов, коленчатого вала, обрыв клапанов, повышенный износ гильз цилиндров и поршней, задир шатунных вкладышей и поршней и т.д.) – 47, ходовая система – 19, электрооборудование – 11, гидросистема – 5, увеличитель крутящего момента – 5, коробка передач – 4, тормозная система – 4, задний мост – 3, остальные узлы – 2. Для зерноуборочного комбайна, %: привод режущего аппарата жатвенной части – 16, цепные передачи молотилки – 14, гидросистема – 7, двигатель – 7, коробки передач – 4, остальные узлы – 52. Значительный процент отказов приходился на долю резинотехнических изделий (шланги высокого давления, резиновые чехлы, уплотняющие манжеты).
Повышение ресурса достигается путем совершенствования конструкций, улучшения уплотнений, введения более тонкой очистки масла, повышения качества материалов и технологических процессов.
9.11. Система проектирования несущих конструкций
9.11.1. Концепция алгоритма МКЭ
Анализ и концепция проблемы механики сплошной среды по МКЭ всегда сводится к так называемому «шаг за шагом» (Step by step process), который имеет огромное практическое значение для использования ЭВМ в целях эффективного расчета. В этом процессе, который можно представить как простой алгоритм, выделяют следующие шесть важнейших шагов [9, 22]:
· дискретизацию сплошной среды;
· выбор интерполяционных функций;
· вычисление характеристик элементов;
· формирование уравнений для сетки конечных элементов;
· решение системы уравнений;
· расчет нужных воздействий.
Особенно важны первые три из шести шагов. Способ дискретизации, выбор вида элементов из общего числа элементов зависит как от природы решаемой проблемы, так и от необходимой точности требуемого решения. Наряду с числом и видом элементов важен и выбор узлов, основных неизвестных в них и интерполяционных функций. С помощью последних определяют поле переменных каждого элемента. От их выбора непосредственно зависит точность аппроксимации. Переменные в элементе могут быть скалярной, векторной или тензорной величиной.
Характеристики отдельных элементов определяются независимо от сетки элементов как единого целого. Так, например, в напряженно-деформационном анализе конструкций основные зависимости между статическими и деформированными величинами устанавливаются для каждого элемента, матрица жесткости формируется автономно для отдельных элементов, а потом на их базе — матрица для всей системы в целом. Поскольку геометрия элементов достаточно проста, то практически это означает, что комплексная проблема разбивается на несколько простых. Характеристики элементов, матрицы жесткости, векторы нагружения и другое вычисляют чаще всего с помощью вариационных принципов на основе принятой геометрии элементов и соответствующих интерполяционных функций. Эти расчеты в основном производятся с применением способа численной интеграции.
|
|
Последние три шага, имеющие большое значение для практических расчетов, приспосабливают к автоматическому режиму ЭВМ. В этой области ведутся исследования, поиск более экономичных решений с меньшим расходом счетного времени ЭВМ. Это прежде всего относится к действиям, связанным с решением больших систем алгебраических уравнений, особенно в области нелинейного анализа, который сводится к решению ряда линейных систем алгебраических уравнений.
9.11.2. Общая архитектура САПР, базирующаяся на МКЭ
Практически расчет характеристик некоторого устройства в процессе проектирования проходит стадию представления задачи уравнениями в частных производных и включает в себя три этапа:
· описание геометрии, физических характеристик, генерацию сети конечных элементов;
· расчет с помощью метода конечных элементов;
· визуализацию и интерпретацию результатов моделирования.
Эти три этапа хорошо разделены и в действительности соответствуют на уровне программного обеспечения трем функциям, выполненным отдельными модулями:
· модулем ввода данных;
· модулем вычислений;
· модулем вывода результатов.
9.11.3. Состав и требования к информационному обеспечению
Модуль ввода предназначен для ввода и подготовки всей информации, необходимой для решения задачи методом конечных элементов. Следует сообщить данные о дискретизации области и представить ее физические характеристики. Модуль ввода должен также осуществлять следующие три функции:
· описание геометрии объекта;
· генерацию сети конечных элементов;
· указание областей и границ.
Генерация сети в области заключается в формировании совокупности узлов и совокупности конечных элементов, обеспечивающих приемлемую дискретизацию области. Такая дискретизация должна соответствовать границам области и внутренним границам между различными ее участками. Кроме того, конечные элементы не должны иметь форму, слишком отличающуюся от симметричных форм стандартных элементов (равносторонних треугольников или тетраэдров, квадратов или кубов).
Узлы определяются их координатами, тогда как элементы характеризуются их типом и перечнем их узлов.
Операция указания областей и границ позволяет уточнить физическое поведение:
· описание физических характеристик материалов (например, модуль упругости, проводимость, теплопроводность);
· описание источников (например, источники тепла, нагрузок);
· описание граничных условий (закрепление конструкций);
· описание начальных условий для времяпеременных задач (состояние системы перед приложением импульса нагрузки).
Обычно эта информация вводится последовательно участок за участком, граница за границей. Связи между участками области и узлами позволяют отразить эту информацию в виде дискретизации области.
9.11.4. Функции модуля вычислений
Модуль вычислений решает одиночное уравнение для вариационной постановки или систему линейных уравнений для проекционной постановки.
Этот модуль получает на входе описание сети, физические характеристики и граничные условия. На выходе он выдает значения искомых величин в каждом узле сети.
Для решения систем уравнений используются два семейства методов: методы точечные или блочные, действующие путем релаксаций, и глобальные матричные методы.
Решение линейных систем осуществляется несколькими возможными способами:
· прямыми методами (Гаусса, Холецкого);
· полупрямыми методами;
· итерационными блочными методами (Гаусса ,Зейделя).
9.11.5. Функции модуля вывода
Модуль ввода позволяет описать задачу, которая затем решается модулем вычислений. Однако полученное решение не может непосредственно использоваться по следующим причинам:
· значения переменных в узлах конечноэлементной сети не всегда имеют четкий физический смысл;
· масса необработанной численной информации, получаемой при вычислении, слишком велика для восприятия пользователем.
Модуль вывода играет двойную роль:
· извлекает значащую информацию. Эта информация может быть связана с локальными величинами или глобальными величинами;
· представляет численную информацию в графической форме для облегчения ее восприятия и интерпретации.
9.11.6. Структура вычислительных комплексов
для использования МКЭ
Программа САПР, базирующаяся на методе конечных элементов, должна включать в той или иной степени разнообразные функции, которые объединены в три модуля.
В программном обеспечении систем автоматизированного проектирования функции ввода и вывода особенно развиты, так как они сокращают время получения данных и оценки результатов в ходе моделирования.
В структуру модуля ввода данных входят устройства подготовки и ввода данных:
· клавиатура и контроль на экране;
· сканер;
· сколка (работа с чертежами на специальном планшете для автоматизированного ввода топологии моделей).
Модуль вычислений реализуется с помощью процессора ЭВМ, обладающего достаточным быстродействием и объемом оперативной памяти, соответствующей порядку систем уравнений, решаемых в процессе выполнения задачи. Порядок систем при решении задач прочности конструкции может достигать 104…105, вследствие чего реализация модуля вычислений требует весьма значительных ресурсов оперативной памяти и памяти на внешних носителях для размещения временных наборов данных, формируемых процессором. В настоящее время для решения этих задач используются процессоры персональных ЭВМ класса Pentium.
Модуль вывода реализуется в виде кодированной печати результатов (принтер), графического вывода на графопостроитель, плоттер и визуальный вывод на экран как графической, так и текстовой информации.
9.11.7. Программное обеспечение задач МКЭ
прочности конструкций
В настоящее время существует ряд пакетов прикладных программ, в которых сопряжены метод конечных элементов и некоторые методы САПР.
Общими их разделами являются документы ввода, библиотеки конечных элементов и документы вывода. Один из самых важных документов — это ввод модели, так как создание модели не программируется. Изыскание оптимальной модели является предметом научного поиска (рис.9.23).
Рис.9.23. Конечно-элементная модель несущей конструкции
зерноуборочного комбайна Д08.010
Вычислительные комплексы, содержащие пакет прикладных программ расчета динамики и прочности механических систем обеспечивают расчет напряжений и деформаций в пространственных конструкциях и деталях, представляемых в виде систем, состоящих из стержней, пластин, объемных элементов, элементов, рассматриваемых как твердое тело, гибких нитей и различных связей при статическом и динамическом характере приложения внешних нагрузок.
Комплексы обеспечивают решение следующих задач:
· расчет деформационных перемещений в конструкциях;
· расчет усилий и напряжений в стержнях, пластинах, оболочках и объемных элементах (при этом обеспечивается расчет как компонент, так и эквивалентных напряжений) и коэффициентов запаса по напряжениям;
· просмотр и вывод на печать отредактированных исходных данных и результатов счета;
· графическое изображение расчетных схем конструкции;
· автоматизированное определение геометрических характе-ристик сечений;
· визуальный контроль данных и диагностику ошибок формирования набора данных;
· создание архива решаемых задач и проведение операций с архивными файлами.
Работа организована в режиме диалога пользователь - ПЭВМ.
Комплексы представляют собой совокупность автономных программ, объединенных единой внутренней формой данных, предназначенной для обмена информацией между программами.
Обмен данными осуществляется через внешние запоминающие устройства (накопители на магнитных дисках) с использованием специальной внутренней формы данных.
АПМ WinStructure 3D представляет собой универсальную систему для расчета рамных, пластинчатых, оболочечных, а также смешанных конструкций конечных элементов.
С помощью программы Вы можете рассчитать произвольную трехмерную конструкцию, состоящую из стержней произвольного поперечного сечения, пластин и оболочек при произвольном нагружении и закреплении. При этом соединение элементов в узлах может быть как жестким, так и шарнирным.
В результате выполненных системой АПМ WinStructure 3D расчетов Вы можете получить следующую информацию:
· нагрузки на концах элементов конструкции;
· карту напряжений по длине стержней и по поверхности пластин и оболочек конструкции;
· перемещения произвольной точки;
· карту распределения напряжений в произвольном сечении стержня;
· для отдельного стержня конструкции - эпюры изгибающих и крутящих моментов, поперечных и осевых сил и т.д.
Расчет с помощью МКЭ в форме метода перемещений включает в себя следующие этапы:
· разбиение конструкций на конечные элементы и подготовку топологической, геометрической и физической информации; установление факторов взаимодействия с окружающей средой;
· построение для выделенных конечных элементов соответствующих матриц (жесткости, масс, теплопроводности и др.) и векторов, определяющих зависимости между реакциями, перемещениями в узлах элемента;
· формирование разрешающей системы линейных алгебраических или дифференциально-алгебраических уравнений;
· решение полученной системы уравнений и установление полей перемещений, внутренних силовых факторов , температуры и т.д.;
· обработку результирующей информации и ее анализ.
Перечисленные этапы поддаются четкой универсальной алгоритмизации, и их программная реализация не вызывает принципиальных затруднений при наличии библиотеки стандартных подпрограмм.
Основные этапы расчета напряженно-деформированного состояния конструкции:
·
|
|
|
|
|
|
реальная конструкция представляется в виде идеализированной системы, состоящей из конечных элементов. Вид конечного элемента (прямоугольный стержень, тонкая пластина, шестигранный объемный элемент и т.д.) выбирается из библиотеки конечных элементов, применяемых для данных расчетов программного комплекса (рис. 9.24);
· для описания всей системы принимается глобальная система координат. Местоположение каждого узла конечно-элементной модели (КЭМ) фиксируется тремя координатами: X, Y, Z.;
· определяются типы опор (кинематические граничные условия). Необходимо задать кинематические граничные условия (заранее известные перемещения) таким образом, чтобы исключить возможность перемещения КЭМ рассматриваемой конструкции как твердого тела во всех направлениях;
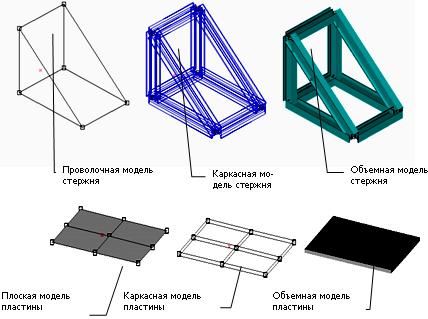
Рис.9.24. Конечные элементы модуля АПМ WinStructure 3D
· нумерация узлов начинается с единицы. Ее порядок определяется только удобствами пользователя;
Рис. 9.25. Напряженное состояние конструкции
· геометрические характеристики самих конечных элементов задаются в локальной (местной) системе координат U, V, W, начало которой для каждого конечного элемента расположено в одном из его узлов;
· результатом расчета является напряженное (рис.9.25) и деформированное (рис.9.26) состояние конструкции, представленное в графическом виде или в виде таблиц.
Рис.9.26. Картина деформированного состояния конструкции
9.12. Примеры и результаты расчета
При проектировании пространственных несущих конструкций очень часто приходится решать задачи нахождения оптимальной конфигурации этих конструкций. Выполнение такого плана расчетов необходимо разбить на несколько этапов:
- составить конечно-элементную модель несущей конструкции, которая представляет собой оболочку, обтягивающую рабочее пространство машины;
- методом удаления отдельных пластин с наименьшим напряжением получить оптимальную конфигурацию несущей системы;
- заменить пластинчатую модель стержневой, оставляя генеральные направления максимальных напряжений;
- провести расчеты стержневой модели;
- по выявленным максимальным напряжениям в стержнях провести расчеты на долговечность конструкции.
Описание задачи
Произвести расчет напряжений в несущей конструкции обоечной машины при нагружении статическими и динамическими нагрузками.*
Ввод данных
А. Задание идентификатора задачи . В этой записи указывается наименование машины:
Запись 1 Длина 30 Тип 0 Имя: Обоечная машина
Обоечная машина ОМВР-1800
Первоначальный вариант конструкции
Оптимизация/Статика/Динамика
Б. Ввод координат узловых точек .
Выбираем правую декартову систему координат с началом, лежащим на оси симметрии конструкции, при этом ось Z направлена вверх (совпадает с главной осью конструкции), оси X и Y лежат в плоскости верхнего пояса рабочей камеры. С помощью сервисных средств программного комплекса применяем дублирование поворота и шага при построении исходной модели.
…
Запись 2 Длина 2080 Тип 132 Имя: Узловые точки
Координаты узлов:
Номер Координаты, мм
узла X Y Z
1 .0000000 267.0000 .0000000
2 .0000000 300.0000 .0000000
3 .0000000 320.0000 .0000000
4 .0000000 320.0000 -22.00000
…
В. Ввод характеристик материала .
Запись 3 Длина 8 Тип 800 Имя: Материал-1
Данные о механических свойствах материала:
Плотность , кг/м3 = 0.780E+04
Модуль упругости, МПа = 0.210E+06
Коэффициент Пуассона = 0.300
Модуль сдвига, МПа = 0.800E+05
Г. Ввод индексов КЭ (конечных элементов).
Запись 5 Длина 5 Тип 399 Имя: Поворот сечен.
Угол поворота сечения стержня, град: 180.
…
Запись 6 Длина 92 Тип 401 Имя: Стойка ++
Индексы стержней Длины жестких вставок, мм
Номер Номера узлов
эл-та I J LI LJ
1* 273 274 .000 .000
2* 274 275 .000 .000
3* 275 276 .000 .000
4* 276 277 .000 .000
5* 277 278 .000 .000
…
Запись 15 Длина 389 Тип 504 Имя: Верхн. лист
Толщина элементов, мм = 5.00
Индексы четырехугольников:
Номер Номера узлов
КЭ
1* 469 470 477 476
2* 470 471 478 477
3* 471 472 479 478
4* 472 473 480 479
5* 473 474 481 480
…
Д. Ввод данных о граничных условиях модели.
…
Запись 18 Длина 16 Тип 50 Имя: Закрепление
Данные о кинематических граничных условиях
Номер Величина и вид Координатная
узла перемещения ось
289 7-шарнирное закрепление —
306 7-шарнирное закрепление —
323 7-шарнирное закрепление —
340 7-шарнирное закрепление —
…
Е. Ввод данных о нагрузках . …
Запись 17 Длина 148 Тип 40 Имя: Сосредоточенные нагрузки
Данные о сосредоточенных узловых усилиях
Номер Величина и вид Координатная
узла усилия ось
17 -31.0 3-усилие ,Н OZ
34 -31.0 3-усилие ,Н OZ
51 -31.0 3-усилие ,Н OZ
68 -31.0 3-усилие ,Н OZ
85 -31.0 3-усилие ,Н OZ
…
На рис. 9.27 представлена КЭ модель обоечной машины.
Рис. 9.27. Исходная КЭ модель несущей конструкции обоечной машины
Получение результатов
Получив и проанализировав результаты расчета построенной модели, приступаем к оптимизации несущей конструкции путем подбора толщин стенок и поперечных сечений модели. Представленная исходная КЭ модель несущей рамы обоечной машины (см. рис.9.27) весит 57,8 кг, после начальной стадии оптимизации вес снизился до 47,7 кг.
Одним из независимых направлений поиска оптимальной конструкции может быть направление, связанное с вычленением зон наименьших напряжений в некоторой оболочке, обтянутой вокруг рабочей зоны, в которой совершается технологический процесс, характерный для данной машины. Для нахождения зон локализации напряжений в несущей системе и создается вспомогательная оболочка в виде поверхности, разбитой на сегменты, которые впоследствии и будут постепенно исключаться до полной оптимизации системы. Вспомогательная поверхность на стадии проектирования дает нам возможность определить места установки несущих элементов (стержни, пластины и т.д.). Оптимизации конструкции по массе можно добиться только при условии, когда несущие элементы системы воспринимают напряжения растяжения‑сжатия, что и обуславливает минимальное поперечное сечение этих элементов при данном нагружении. Обеспечение условия благоприятного нагружения для каждого несущего элемента конструкции приводит к минимальной металлоемкости всей рассматриваемой системы что является основным критерием для проектировщика при создании машины.
Проектирование оптимальной несущей конструкции начинается с рассмотрения всех существующих объектов, которые будут непосредственно воздействовать на систему. Под объектами в данном случае подразумеваются рабочие органы машины, ее приводные элементы, системы подачи и вывода обрабатываемого продукта. Выявляем все точки опор, креплений как отдельных объектов системы, так и всей несущей конструкции в целом. Очень важно определить габариты зон, обслуживающих совокупность объектов рассматриваемой системы: зона рабочих элементов, зона подключения систем питания и отвода продукции, зоны обслуживания и ремонта.
После построения совокупности объектов системы производится соединение опорных точек кратчайшими отрезками, которые и будут являться образующими сложной поверхности, обтягивающей элементы проектируемой машины.
К конечно-элементной модели прикладываются статические и псевдодинамические экстремальные нагрузки, характеризующие эксплуатационный режим проектируемой машины. Анализ этих возможных вариантов нагружения позволяет выбрать краевые условия.
Согласно краевым условиям нагружения на любом пакете, реализующем метод конечных элементов, необходимо получить картину напряженно-деформированного состояния вспомогательной оболочки, которая и является исходным материалом для поиска наилучшей конфигурации несущей системы. Исключая зоны с наименьшими деформациями, тем самым производим стягивание поверхности оболочки до пространственного контура с заданной градацией уровня напряжения. Дальнейшая работа конструктора заключается в замене вспомогательной оболочки с вырезанными окнами на стержневую или пластинчато-стержневую конструкцию.
Предложенный подход позволяет за короткий промежуток времени провести сравнительный анализ проектируемой конструкции и с наименьшими затратами найти оптимальный вариант построения объемной несущей системы на ранней стадии жизненного цикла машины.
Поэтому, проведя первый этап оптимизации, переходим к нахождению оптимальной ориентации несущих стержней с помощью вспомогательных поверхностей, «обтягивающих» рабочие органы, рис. 9.28, 9.29.
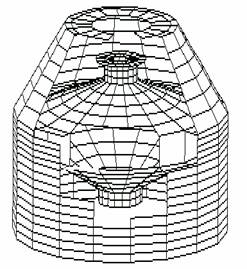
Рис. 9.28. Вспомогательные поверхности
несущей конструкции машины
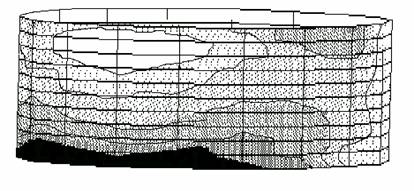
Рис.9.29. Напряженное состояние несущей вспомогательной поверхности
С помощью анализа распространения полей напряжений по вспомогательной поверхности устанавливаем несущие стержни в зонах максимального напряжения (рис. 9.30).
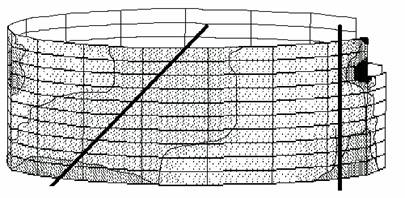
Рис.9.30. Расположение несущих элементов
После установки стержней в местах сосредоточения полей и просчета нескольких вариантов получаем окончательный вес конструкции – 24,0 кг. Сравнивая начальную конструкцию несущей рамы и оптимизированную, получаем уменьшение массы в среднем на 58%, рис.9.31.
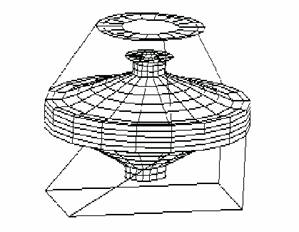
Рис.9.31. Оптимальная конструкция несущей рамы
обоечной машины ОМВР-1800
После проведения оптимизации получаем два варианта конструкции, которые отличаются не только по массе, но и по трудоемкости изготовления. Поэтому необходимо сравнить этот показатель в предположении того, что сварка конструкции будет производиться ручной электродуговой сваркой. Расчет проводим по следующей формуле:
![]() ,
,
где t — удельная трудоемкость сварки 1 пог. м швов различного вида разного сечения; l - длина швов различного сечения.
Исходный вариант:
![]() нормочаса.
нормочаса.
Оптимизированный вариант:
![]() нормочасов.
нормочасов.
Трудоемкость изготовления оптимизированной конструкции не намного отличается от исходной, что почти не скажется на последующей стоимости всей конструкции с точки зрения затраченной трудоемкости на сварку.
Расчет ресурса несущей рамы
На этапах проектирования машины, которые предусматривают изготовление опытного образца или опытной партии машин, производят прогнозирование ресурса на базе предварительных экспериментальных исследований. Экспериментально-расчетный метод прогнозирования ресурса является более точным, чем чисто расчетный, потому что он основан на экспериментальных методах об эксплуатационной нагруженности исследуемых конструкций, их потенциальных свойствах и учитывает прототип технологии производства.
Экспериментально-расчетный метод прогнозирования ресурса связан с решением двух основных задач:
- создание модели напряженного состояния несущей конструкции на базе экспериментальных данных;
- прогнозирование ресурса несущей конструкции по полученной модели напряженного состояния.
Исчерпание ресурса силовых конструкций связано главным образом с накоплением необратимых повреждений усталостного характера. Прогнозирование повреждений усталостного характера базируется на статистических моделях напряженного состояния несущих конструкций. Основой для создания статических моделей напряженного состояния конструкций являются натурные эксперименты с образцами машины или их физическими моделями.
Для расчета ресурса конструкции по условию накопления усталостного повреждения при воздействии переменных напряжений случайной величины необходимо располагать эмпирическим (гистограмма) или теоретическим (закон) распределением амплитуд напряжений, эквивалентных по своему действию реальному процессу. С этой целью исходный процесс изменения напряжений во времени схематизируется. Наиболее точным считается схематизация по методу «полных циклов».
Алгоритм схематизации процессов изменения напряжений по методу «полных циклов» реализован в пакете прикладных программ под названием SPD7 (разработан на кафедре ОКМ ДГТУ). В программе существует банк данных амплитуд после натурных испытаний различных машин и механизмов.
Расчет среднего ресурса производится по условию начала образования усталостной трещины длиной 0,2…0,5 мм при многоцикловом нагружении N = 50000 циклов. Расчет ресурса базируется на линейной гипотезе суммирования усталостных повреждений. Исследования С.В. Серенса и В.П. Когаева показали, что следует корректировать сумму относи-тельных долговечностей с учетом вероятности появления больших амплитуд напряжений. Практика показала что расчет ресурса по корректированной линейной гипотезе суммирования повреждений Серенса-Когаева более точно прогнозирует реальный ресурс.
Тогда средний ресурс для эмпирического распределения амплитуд напряжений
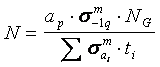 ,
,
где ap - расчетная сумма относительных долговечностей; ![]() - медианное значение предела выносливости натурной детали на множестве всех планок металла данной марки и возможных отклонений размеров и технологий изготовления в пределах допусков; NG - абсцисса точки перелома кривой усталости (базовое число циклов); m - показатель угла наклона левой ветви кривой усталости;
- медианное значение предела выносливости натурной детали на множестве всех планок металла данной марки и возможных отклонений размеров и технологий изготовления в пределах допусков; NG - абсцисса точки перелома кривой усталости (базовое число циклов); m - показатель угла наклона левой ветви кривой усталости; ![]() - среднее значение амплитуды напряжений i –й ступени гистограммы; ti - относительное число повторений амплитуды
- среднее значение амплитуды напряжений i –й ступени гистограммы; ti - относительное число повторений амплитуды ![]() .
.
Значения ap берут по рекомендациям ВИСХОМа. Для силовых конструкций можно принять ap » 0,1–0,2.
Расчет функции распределения ресурса для всех деталей парка машин производится на основании предположения, что ее форма представляет собой логарифмически нормальный закон.
Тогда функция распределения ресурса
![]() ,
,
где ТР - ресурс, соответствующий вероятности разрушения р;uР - квантиль нормального распределения; dlgT - среднее квадратическое отклонение логарифма ресурса.
Средний ресурс в часах определяется:
![]() ,
,
где n - эффективная частота повреждающих амплитуд напряжений, Гц; n - число повреждающих амплитуд напряжений; t - время записи при натурном измерении, с.
![]() ,
,
где ![]() - коэффициент вариации предела выносливости,
- коэффициент вариации предела выносливости, ![]() = 0,08…0,15;
= 0,08…0,15; ![]() - коэффициент вариации максимальных амплитуд напряжений,
- коэффициент вариации максимальных амплитуд напряжений, ![]() = 0,08…0,15.
= 0,08…0,15.
Программа SPD7 ведет расчет по приведённым формулам.
Из опыта проведения испытаний несущих конструкций подобного типа для несущей рамы обоечной машины ограничимся частотами l = 0,001…5 Гц.
Форму и зависимость возникновения нагрузок берем из банка данных случайных процессов по результатам испытаний сельскохозяйственной техники (рис.9.32).
В соответствии с принятой l=5 Гц произведем фильтрацию случайного процесса (рис.9.33) и построим его гистограмму (рис.9.34). Методом полных циклов схематизируем процесс (рис.9.35) и произведем расчет ресурса конструкции для 98%-ной вероятности безотказной работы (рис.9.36).
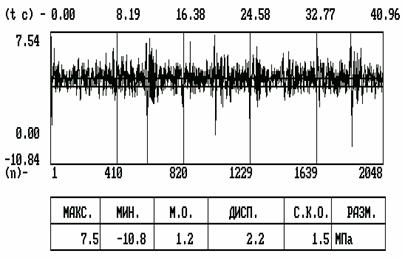
Рис.9.32. Случайный процесс из банка данных
для стационарных машин
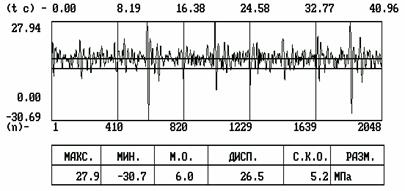
Рис.9.33. Случайный процесс после
фильтрации шумов
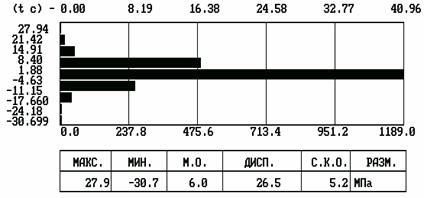
Рис. 9.34. Гистограмма и статистические
характеристики случайного процесса
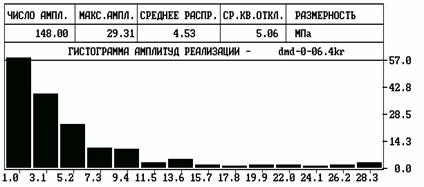
Рис.9.35. Гистограмма амплитуд реализации
напряжений по методу полных циклов
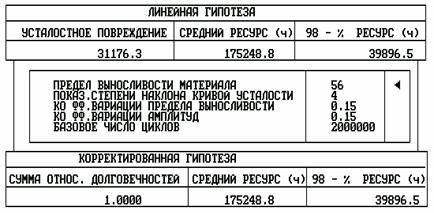
Рис.9.36. Расчет ресурса по эмпирическому
распределению амплитуд напряжений
Функция распределения ресурса построена как прямая линия в вероятностно-логарифмических координатах, проходящих через две точки значения ресурса Т50 и Т98 (рис.9.37).
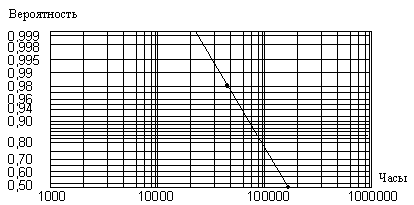
Рис.9.37. Функция распределения ресурса в несущей раме при пределе выносливости 56 МПа
* Расчет несущей конструкции обоечной машины ОМВР-1800 выполнен студентом КП-5-26 М.М. Черкашиным в 1997 г.
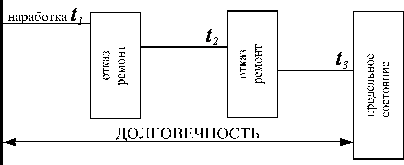

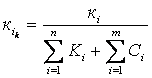
 ,
,