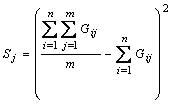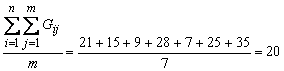5.1 - Прогнозирование, классификация методов прогнозирования.

5.2 - Классификация методов научно-технического прогнозирования.

5.3 - Прогнозирование на основе построения линии жизненного цикла технических объектов.

5.4 - Прогнозирование на основе  построения огибающих кривых.

5.5 - Прогнозирование функциональных характеристик технических систем на глубину 20 и более лет.

5.6 - Прогнозирование  функциональных параметров машин на основе анализа патентной активности.

5.7 - Прогнозирование направления развития сельскохозяйственных машин.

Важной информацией, необходимой при проектировании объектов, являются тенденции развития их основных технических показателей.

Прогноз – это конкретное предсказание, суждение о состоянии какого-либо явления в будущем на основе специальных исследований.

Прогнозирование (от греческого proghosis – предвидение, предсказание)– это научная деятельность, направленная на влияние и изучение возможных альтернатив будущего развития и структуры его вероятных траекторий. Каждая альтернативная траектория развития связывается с наличием комплекса внешних относительно исследуемой системы (явления) условий [41, 44]. Объектом прогнозирования, естественно, не могут являться любые явления или процессы. Если результат процесса однозначен, то его прогнозирование не имеет смысла. Напротив, если имеется множество возможных альтернатив для реализации процесса, то прогноз дает новую информацию.

5.1.1. Разновидности прогнозов

В правительственных учреждениях, в промышленности и науке наиболее востребованы следующие прогнозы: развитие техники; ресурсов; спроса; промышленного потенциала; демографической ситуации. По принадлежности к области знания прогнозы разделяют на научно-технические, инженерные, экономические. В свою очередь эти прогнозы расчленяется на этапы: исследовательский;  программный; организационный.

Исследовательские прогнозы – определяют новые возможности и перспективные цели развития науки и техники. Заключительной, наиболее трудной и ответственной стадией разработки исследовательского прогноза является оценка гипотетической результативности или, иначе говоря, значительности возможных целей научно-технического прогресса. На основе исследовательского прогноза разрабатывается программный прогноз.

Программные прогнозы – формируют программы, эффективные направления и последовательности действий, направленные на достижение целей развития науки и техники. При этом дается оценка возможных сроков, очередности достижения поставленных целей развития.

Организационные прогнозы – основываются на общих закономерностях, тенденциях развития науки, с учетом исследовательского и программного прогнозов. При их разработке используется информация как о потребностях, так и о возможностях общества. Задачей этого вида прогнозов является определение следствий конкретных вариантов действий, а также оценка ресурсов, необходимых для выполнения в прогнозируемый период программ исследовательских (НИР) и проектно-контрольных работ (ОКР). Организационные прогнозы позволяют увязать всю систему научно-технических прогнозов с планами и создают предпосылки для привлечения необходимых ресурсов.

 Научно-технический прогноз. Объектом научно-технического прогнозирования, в частности, является направление развития машин и оборудования. Важным аспектом этого прогноза является оценка потребных сырьевых и экономических ресурсов, а также оценка социальной и экологической ситуации при реализации прогнозируемых направлений развития.

Инженерный прогноз основан на анализе предложений на рынках оборудования, выставочного ассортимента машин и оборудования, тематики публикаций в специализированных изданиях, динамики и структуры потока патентуемых изобретений. На современном этапе для этого используют средства и методы информационного слежения за потоком публикации и сообщений на основе автоматизированных информационных систем за конкретными областями научно-технического прогресса и систематически уточняемых перспектив их развития.

В инженерной деятельности разработчика новой техники инженерный прогноз используют на этапах НИР и на ранних этапах проектирования (ОКР). Кроме этих прогнозов, на этапах проектирования выполняются прогнозы надежности и безотказности работы и прогнозы технико-экономических характеристик проектируемых машин.

Экономический прогноз - это система научных исследований о направлениях развития экономики и отдельных ее элементов. Он использует прогноз развития науки и техники, прогноз изменения демографической ситуации, прогноз освоения природных ресурсов, изменение окружающей среды.

Научно-технический, инженерный, экономический прогнозы взаимосвязаны друг с другом,  взаимно дополняют и определяют друг друга.

5.1.2 Эшелоны прогнозов

По времени упреждения, с позиции футурологии, прогнозы разделяются на текущие, краткосрочные, среднесрочные, долгосрочные и сверхдолгосрочные.

Текущий прогноз - правомерен, когда не ожидается существенных изменений исследуемого объекта, а имеются в виду лишь отдельные частные количественные оценки. Глубина такого прогнозирования – 5 лет.

Краткосрочный прогноз - рассчитан на перспективу до 5-10 лет. Условия прогноза исходят из существующей тенденции развития науки и техники и количества выполняемых научных работ. За этот период удвоится количество средств производства, окончится срок действия большинства нынешних патентов и т.д. Очень важным обстоятельством является и то, что в этот период времени выявленные наукой факторы явления и принципы переходят из раздела фундаментальных наук в прикладные, оттуда к разработчикам и далее, через опытно-промышленную проверку к стадии массовой реализации соответствующих нововведений.

Важным является и то обстоятельство, что в течение этого периода времени на передовые позиции научно-технического прогресса выходит новое поколение специалистов. Прогнозы этого типа основываются обычно на вполне определившихся в настоящее время тенденциях НТП. Эти прогнозы содержат, как правило, не только количественные,  но и структурные, и качественные оценки. Прогноз краткосрочный регламентирован ОСТ 23.2.484-78.

Среднесрочный прогноз - рассчитан на срок до 10-15 лет. За это время произойдет удвоение как общего объема принятых в современной науке концепций, теорий и методов, так и численности населения земного шара. В таких прогнозах количественные оценки уступают место качественным. Предметами подобных прогнозов не редко являются уже не экономические возможности, а фундаментальные законы естествознания. К тому же, ученый, разрабатывающий подобный прогноз, уже не может ограничиться своей конкретной отраслью знания, а должен исходить из более широкой системы научных знаний.

Долгосрочный прогноз -  рассчитан на срок 15-20 и более лет. Такие прогнозы носят, как правило, чисто предположительный, гипотетический характер, учитывая, что все ученые в столь отдаленном будущем будут руководствоваться новыми научными представлениями, многие аспекты которых нам пока неизвестны. Современный прогнозист при разработке таких прогнозов полагается скорее на свои взгляды и творческую фантазию, чем на определенную систему научных представлений. Количественные оценки здесь отсутствуют, а качественные оценки и структурные предположения ограничиваются лишь рамками наиболее общих вопросов естествознания. Представители данных прогнозов – это писатели-фантасты. Данный прогноз не всегда целесообразен, так как чрезмерно большим становится разрыв между профилем и фоном исследования, а также между условным предсказанием и возможным многократным изменением объекта прогнозирования. Научные предвидения в этом случае ограничиваются рамками общих законов развития природы и общества.

Сверхдолгосрочный прогноз. В этом прогнозе присутствуют только качественные оценки и “прозрение” отдельных ученых и писателей-фантастов. Примером этого являются предвидения Жюль Верна, Герберта Уэльса.

5.1.3. Оценка приемлемой глубины прогнозов

Количественной мерой опережения современности является глубина прогноза. Для формирования конкурентных преимуществ, достигаемая нами глубина прогноза должна обеспечить так называемый «горизонт свободного прогноза». Горизонт свободного прогноза это отрезок времени, представляющий собой разность времени достигнутого при прогнозе и времени, необходимого для реализации мероприятий, принятых по результатам прогноза. Горизонт свободного прогноза призван сформировать у разработчика конкурентные преимущества, необходимые для завоевания новых рынков, удержания достигнутых на рынке позиций.

Количественной мерой заблаговременности выполнения проектно-конструкторских работ будет глубина прогноза или эшелоны прогнозирования. Возможная и потребная глубина прогноза для разных областей науки и техники и объектов прогнозирования различна. Результаты соответствующих исследований по этой проблеме приводятся в табл.5.1.

Таблица 5.1

Требуемая и фактически достигаемая глубина прогноза

для различных областей и объектов прогнозирования

Области и объекты прогнозирования	Требуемая глубина прогнозов, лет	Фактически достигаемая глубина прогнозов, лет
Объем доступных для разработки природных ресурсов Нововведения с ярко выраженными социальными последствиями (автоматизация, компьютеризация, средства связи, транспорт, проекты городов и т.д.) Ядерная энергетика Космические программы Вооружение Показатели, характеризующие развитие национальной экономики Массовое и крупносерийное производство новых технических средств Производство новых потребительских товаров	50 и более 30…50 25 25…30 20…25 20 20 5…10	25…35 7…30 10…12 10…12 7…10 5…7 5…7 3…5

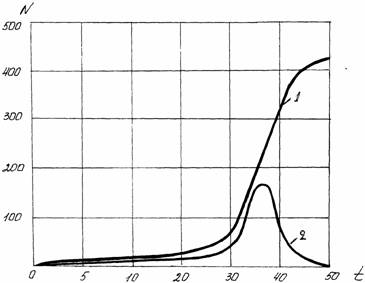
Для получения устойчивых конкурентных преимуществ на рынке технических средств необходимо создать новое изделие, а не модификацию уже известной техники на данном рынке. Для получения нового изделия необходимо накопить интеллектуальный потенциал от 50 до 500 изобретений и открытий. На это, по оценкам зарубежных исследователей, требуется от 20 до 70 лет. А по оценкам отечественных исследователей А.И.Русакова, О.А. Пенязева, весь жизненный цикл конструктивного решения (с момента зарождения идеи до снятия ее с эксплуатации вследствие устаревания положенной в основу концепции) проходит 50-60 лет. По целому ряду направлений разработки новой техники этот период может быть сокращен в 2-3 раза.

В работах Г.С.Альтшуллера и А.Ф.Каменева указывается на неравномерный характер патентной активности в течение жизненного цикла (рис.5.1).

Рис.5.1. Оценка патентной активности за жизненный цикл изделия:

N – количество патентов, t – годы; 1 – интегральная оценка;

2 – дифференциальная оценка

На рис.5.1 представлены интегральная и дифференциальная оценки патентной активности конструкции, из которого следует, что на первые 50 патентов уходит более 25 лет развития конструкции, а на пике патентной активности, соответствующей широкому и повсеместному внедрению конструкции, на это потребуется менее полугода.

По результатам исследований А.Д. Чистякова [47], 20 лет – это минимальная глубина прогноза при разработке новых машин и оборудования, позволяющая накопить научный и патентный потенциал, гарантирующий конкурентные преимущества.

Научное прогнозирование насчитывает в настоящее время около 140 различных по уровню, масштабам и научной обоснованности методов и приемов прогнозирования научно-технического развития. Действительное число методов, используемых в регулярной практике,  значительно меньше.

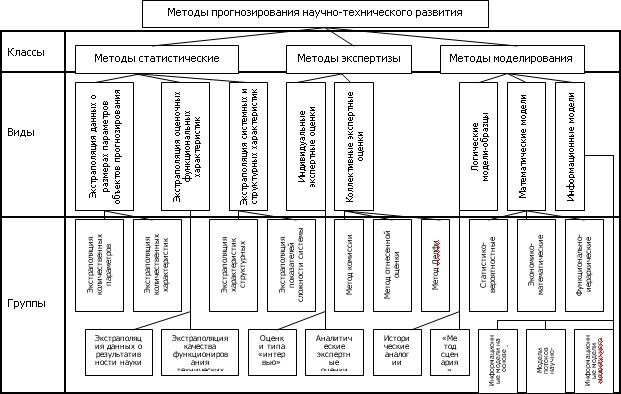
Рис.5.2. Общая классификация научно-технического прогнозирования

Практически, наиболее целесообразно, эти методы сводятся в три основных класса (рис. 5.2):

1. Методы статистические.

2. Методы экспертизы.

3. Методы моделирования.

При этом каждый из основных классов включает в себя по несколько видов и характерных групп методов научного прогнозирования.

Основным видом статистического прогнозирования является экстраполяция. Методологической основой статистической экстраполяции тенденций является представление о развитии объекта прогнозирования как о неразрывной связи прошлого, настоящего и будущего его состояния (инертность развития), использование выявленных закономерностей за предшествующий период и в определении их на последующий период.

Понятие тенденции развития не имеет достаточно четкого определения. Принято под тенденцией развития понимать некоторое общее направление развития, долговременную эволюцию. Обычно тенденцию стремятся представить в виде гладкой траектории. Предполагается, что такая траектория, которую можно охарактеризовать в виде некоторой функции времени, назовем ее трендом, характеризует основную закономерность движения во времени и в некоторой мере (но не полностью) свободна от случайных воздействий. Тренд описывает фактическую усредненную для периода наблюдений тенденцию изучаемого процесса (технического показателя и др.) по времени, его внешнее проявление.

При наличии достаточного количества статистических данных (банк данных) (например, минимальное число данных для линейного, параболического и кубического трендов соответственно 6, 13 и 23) и при предлагаемом сохранении технологии и принципов работы машин (устройств и др.) тренд описывается математическим выражением (математическая модель). При этом метод прогнозирования заключается в экстраполяции, т.е. в продлении в будущее тенденции, наблюдаемой в прошлом.

При этом важным методическим обстоятельством рассматриваемого класса прогнозирования является выбор соотношения глубины ретроспекции экстраполируемой тенденции (базы экстраполяции – основания прогноза) и дальности экстраполируемого интервала.

При прогнозировании показателей технического уровня тракторов и сельскохозяйственных машин необходимое время ретроспекции   устанавливается из условия

,                                (5.1)

где  - время упреждения прогноза (время экстраполяции).

При известном времени ретроспекции время экстраполяции

.                                 (5.2)

При этом различают: краткосрочный прогноз (5-10 лет), среднесрочный прогноз (10-15 лет), долгосрочный прогноз (15-25 лет).

Весьма распространены методы прогнозирования, связанные со сбором и систематизацией экспертных оценок.

Эксперт – это специалист в конкретной области науки или техники, у которого имеется гипотетическое представление о путях разрешения нынешних противоречий процессов, априорных оценок значимости различных решений науки и практики и интуитивных догадок об альтернативах и возможностях вариантах развития.

Методологической основой использования методов экспертных оценок при прогнозировании является отсутствие достаточного количества статистических данных (например, новое направление в науке или технике), а также прогнозирование некоторых аспектов развития, которые не имеют количественных оценок (например, пути решения технической проблемы, оценка вероятности использования в технике (в ожидаемые сроки) различных открытий и др.).

Основой экспертных оценок, полученных коллективом экспертов, является процедура сбора прогнозной информации, определение степени согласованности мнений экспертов по конкретным перспективам развития и оценка некоторых аспектов развития (прогнозирование). Методика организации проведения опроса экспертов и методы обработки полученной информации разработаны достаточно глубоко [49].

Большое значение приобретают в настоящее время методы прогнозирования, основанные на математических и информационных моделях (методы моделирования). При этом строятся модели, основанные на изучении внутренней логики развития конкретной научной дисциплины (историко-логические модели), информационные модели (например, моделирование информационных сигналов, содержащихся в потоке патентных документов о мировом техническом опыте в каком-либо конкретном направлении), функционально-иерархические модели, одним из простейших которых являются модели, описывающие закономерности работы (функционирования) технического объекта, позволяющие прогнозировать направления развития и кратчайшие пути достижения поставленных целей развития.

5.2.1. Метод экспертных оценок

Существует большое количество методов экспертной оценки [49]. Рассмотрим один из наиболее часто используемых.

Оценка качественного состава экспертной комиссии, как указывалось выше, процесс формирования экспертной группы и подготовка экспертов к измерениям – весьма важные и ответственные этапы. Применение экспертного метода предполагает соблюдение следующих условий:

- экспертная оценка должна производиться только в том случае, когда нельзя использовать для решения вопроса более объективные методы;

- в работе экспертной комиссии не должно быть факторов, которые могли бы влиять на искренность суждений экспертов, мнения экспертов должны быть независимыми;

- вопросы, поставленные перед экспертами, не должны допускать различного толкования;

- эксперты должны быть компетентны в решаемых вопросах;

- количество экспертов должно быть оптимальным;

- ответы должны быть однозначными и обеспечивать возможность их математической обработки.

Качественный состав экспертной комиссии – важное условие эффективности экспертного метода. Вполне очевидно, что во всех без исключения случаях экспертиза должна проводиться грамотными, высококвалифицированными, компетентными и достаточно опытными специалистами. Весьма полезно их предварительное специальное обучение и совершенно необходим инструктаж. На завершающем этапе формирования экспертной группы целесообразно провести тестирование, самооценку, взаимооценку экспертов и проверку согласованности мнений.

Тестирование состоит в решении экспертами задач, подобных реальным, с известными (но не экспертам) ответами. На основании результатов тестирования по критерию Р.А.Фишера проверяется равноточность отсчетов, даваемых экспертами, устанавливается их компетентность и профессиональная пригодность.

Самооценка экспертов состоит в том, что каждый из них в строго ограниченное время отвечает на вопросы специально составленной анкеты, в результате чего быстро и просто проверяет свои профессиональные знания и деловые качества по балльной системе. При всей субъективности такой оценки опыт показывает, что экспертные группы с высокими показателями самооценки экспертов ошибаются в меньшей степени.

Весьма показательной является взаимная оценка экспертами друг друга (также по балльной системе). Для этого, разумеется, необходим опыт совместной работы.

При наличии сведений о результатах работы эксперта в других экспертных группах критерием его квалификации может стать показатель или степень надежности – отношение числа случаев, когда мнение эксперта совпало с результатами экспертизы, к общему числу экспертиз, в которых он участвовал. Использование этого подхода к отбору экспертов требует накопления и анализа большого объема информации, но открывает возможность непрерывного совершенствования качественного состава эксперт - групп.

На заключительном этапе подготовки экспертной комиссии согласованность мнений экспертов, включенных в ее состав, определяют по общему для всей комиссии показателю качества – коэффициенту конкордации

,                                  (5.3)

где

;      ,

где  - сумма квадратов отклонений суммы рангов каждого объекта экспертизы от среднего арифметического суммырангов;  - число экспертов;  - число объектов экспертизы;  - ранг оценки    -м экспертом -го объекта экспертизы.

В зависимости от степени согласованности мнений эксперта коэффициент конкордации может принимать значения от 0 (при отсутствии согласованности) до единицы (при полном единодушии).

ПРИМЕР. Определить степень согласованности мнений пяти экспертов, результаты ранжирования которыми семи объектов экспертизы приведены в табл.5.2.

Таблица 5.2

Результаты промежуточных вычислений

Решение.

1. Составим вспомогательную табл. 5.2.

2. Среднее арифметическое рангов

.

3. Используя результаты промежуточных вычислений, приведенные в табл.5.2, получим

=630.

4. Коэффициент конкордации

.

Степень согласованности мнений экспертов можно считать удовлетворительной.

Если степень согласованности мнений экспертов оказывается неудовлетворительной , принимают специальные меры для ее повышения. Сводятся они, в основном, к проведению тренировок с обсуждением результатов и разбором ошибок. Если возможности для предварительной подготовки экспертов нет, измерение проводится по методу Дельфы. Характерными чертами этого метода являются:

- анонимность – эксперты не встречаются друг с другом, чтобы избежать влияния авторитета и красноречия кого-либо из них;

- многоэтапность – после каждого тура опроса эксперты знакомятся с мнениями друг друга и при необходимости представляют письменные обоснования своих точек зрения. Соглашаясь или не соглашаясь с мнениями коллег, они могут пересматривать свою точку зрения;

- контроль – после каждого тура проверяется согласованность мнений экспертов до тех пор, пока разброс отдельных мнений не снизится до заранее выбранного значения.

При особо ответственных измерениях экспертным методом могут учитываться весовые коэффициенты квалификации экспертов.

Количество экспертов тоже играет важную роль. С ростом числа экспертов в группе точность измерения повышается. Это фундаментальное свойство любого многократного измерения известно и используется для определения численности экспертной группы , обеспечивающей заданную точность измерения.

Экспертная оценка по методу весовых коэффициентов. Смысл метода весовых коэффициентов в том, что объекты, подлежащие экспертизе – экспертной оценке значимости объекта в представленной выборке объектов, представляются каждым экспертом в виде ранжированного ряда, определяющего место объекта в выборке. Статистическая обработка ранжированных объектов позволяет оценить весовые коэффициенты объектов. Величина весовых коэффициентов определяет прогнозную экспертную оценку значимости объекта в представленной выборке. Обычно порядок действий при этом бывает следующий.

1. Объекты экспертизы располагаются в порядке их предпочтения (ранжирование). Место, занятое при такой расстановке в ранжированном ряду, называется рангом.

2. Наиболее важному объекту приписывается балл или весовой коэффициент, равный 1; всем остальным в порядке уменьшения их относительной значимости – баллы или весовые коэффициенты от 1 до 0.

3. Сопоставляется первый объект с совокупностью всех остальных. Если, по мнению эксперта (экспертов), он предпочтителен, чем совокупность всех остальных вместе взятых, то результат измерения в баллах или весовой коэффициент корректируется в сторону увеличения с таким расчетом, чтобы он стал больше (иногда определяют и насколько больше) суммы баллов или весовых коэффициентов всех остальных объектов экспертизы, которые ниже рангом. В противном случае результат измерения или весовой коэффициент первого объекта корректируется в сторону уменьшения так, чтобы он оказался меньше суммы баллов или весовых коэффициентов остальных объектов.

4. Сопоставляется второй объект с совокупностью всех остальных, стоящих ниже рангом. По установленному выше правилу корректируется результат его измерения или значение весового коэффициента (при этом нужно следить, чтобы не нарушилось предпочтение первого объекта перед совокупностью всех остальных, если оно установлено на предыдущем этапе). Такая процедура сопоставлений и корректировок продолжается вплоть до предпоследнего объекта.

5. Полученные результаты измерений или весовые коэффициенты нормируют, то есть делят на общую сумму баллов или весовых коэффициентов. После этого они принимают значения в пределах от 0 до 1, а их сумма становится равной 1.

Вся эта процедура проделывается при уточнении ранжированного ряда. (Этот метод впервые был предложен в начале 1950-х годов американскими учеными Т.Дж. Гордоном и О. Хелмером для решения военных проблем. Идеология его происходит из древнегреческого города Дельфы, где по преданию при храме Аполлона с IX в. до н.э. по IV в н.э. существовал совет мудрецов («дельфийский оракул»), славившийся своими предсказаниями.

Результат многократного измерения экспертным методом весовых коэффициентов должен учитывать мнения всех экспертов (все результаты однократных измерений)). Значения весовых коэффициентов  в таком случае рассчитывают по формуле

. (5.4)

 

 

ПРИМЕР. Мнения пяти экспертов о семи объектах экспертизы выражены следующим образом:

1-й эксперт:      ;

2-й эксперт:      ;

3-й эксперт:      ;

4-й эксперт:      ;

5-й эксперт:      .

По сумме рангов каждого объекта экспертизы построить ранжированный ряд, являющийся результатом многократного измерения. Определить весомость членов ряда.

Решение.

1. Сумма рангов

 равна 4+6+4+4+3=21;

 равна 3+3+2+3+4=15;

 равна 2+2+1+2+2=9;

 равна 6+5+6+5+6=28;

 равна 1+1+3+1+1=7;

 равна 5+4+5+6+5=25;

 равна 7+7+7+7+7=35.

Результат многократного измерения имеет вид:

.

2. По формуле (5.4) величина весовых коэффициентов:

;          ;          ;

;           ;          ;

;

.

Минимальный весовой коэффициент у объекта №5, максимальный – у объекта №7.

5.2.2. Статистическое прогнозирование показателей

технического уровня сельскохозяйственных машин

Для прогнозирования численных значений показателей технического уровня тракторов и сельскохозяйственных машин (СХМ) целесообразно применять методы статистического прогнозирования – экстраполяции тенденций при условии наличия достаточного банка статистических данных и при предполагаемом сохранении технологии и принципов работы машин.

В зависимости от специфических особенностей и целевого назначения сельхозмашин прогнозирование показателей их технического уровня должно осуществляться по подгруппам и видам машин.

Учитывая, что сложные СХМ, как правило, не могут быть охарактеризованы одним показателем, в качестве основных показателей технического уровня СХМ используются следующие:

- производительность за час чистого времени;

- масса машин;

- мощность двигателей;

- универсальность;

- дорожный просвет;

- ширина захвата;

- рабочая скорость движения агрегата на основных операциях;

- коэффициент использования рабочего времени смены;

- коэффициенты надежности выполнения технологических процессов;

- среднесменное время технического обслуживания.

Структура прогнозирования численных значений показателей технического уровня СХМ представляет собой совокупность следующих этапов:

1. Выбор номенклатуры тракторов и СХМ и прогнозируемых показателей технического уровня.

2. Выявление и анализ тенденций развития.

3. Выбор формы кривых роста, описывающих закономерности развития прогнозируемых показателей.

4. Оценка параметров кривых роста, построение тренда.

5. Экстраполяция тренда и доверительные интервалы прогноза.

6. Оценка результатов прогнозирования.

Рассмотрим прогнозирование показателей технического уровня на примере основных видов зерноочистительных машин.

5.2.2.1. Выявление и анализ тенденций развития

Для выявления анализа тенденций развития основных показателей технического уровня СХМ необходимо проанализировать рассматриваемые машины, выпускаемые фирмами разных стран мира или только Российской Федерацией. При анализе и систематизации технических показателей этих машин в банки статистических данных необходимо учитывать их однородность и сопоставимость. Основой разбиения этих машин по видам и соответствующих им технических показателей является, как правило, целевое назначение этих машин (зерноуборочные комбайны, воздушно-решетные машины первичной очистки и др.).

Полученные динамические ряды – зависимости величин показателей технического уровня от времени (банки статистических данных) необходимо проанализировать на наличие статистически значимой разности этих показателей от времени. Решение этой задачи основывается на статистической проверке гипотез [44].

Наиболее простой подход заключается в разбиении анализируемого ряда на две примерно равные по числу членов части, каждая из которых рассматривается как некоторая самостоятельная выборочная совокупность данных. Испытание разности средних, исчисленных для каждой их этих совокупностей, покажет, существенно ли различаются между собой средние (т.е. существенна ли зависимость величины показателя от времени), или это расхождение не превышает доверительного интервала ряда случайных величин (т.е. не существует статистически значимого различия величины показателя в рассматриваемый отрезок времени).

Можно воспользоваться методом проверки, разработанным для малых выборок (предполагается, что они имеют нормальное распределение).

Ряд разбивается на две части, каждая из которых рассматривается как две выборки. Первая имеет среднюю , вторая . Необходимо проверить гипотезу о существенности разности . Проверка этой гипотезы проводится по -критерию Стьюдента [18], применение которого правомерно при однородности дисперсий двух исследуемых совокупностей  и .

Проверка однородности дисперсий реализуется с помощью -критерия Фишера [18], который основан на сравнении расчетного отношения

 (где )                           (5.5)

с табличным , величина которого выбирается для заданного уровня значимости  (для анализа функциональных зависимостей используют  или ) и числа степеней свободы числителя (большая из дисперсий)  и знаменателя  ( и  - соответственно число показателей в первой и второй выборке). Если , при заданном уровне доверительной вероятности, то гипотеза о равенстве дисперсий  и  принимается, в противном случае  - отклоняется и, следовательно, использование -критерия Стьюдента для оценки разности средних невозможно.

При выполнении условия () расчетное значение -критерия определяется из выражения

,

где  - среднее квадратическое отклонение разности средних,

.

При  гипотеза о зависимости величин показателя  от времени принимается, в противном случае  - отвергается (здесь  - табличное значение -критерия Стьюдента при заданном уровне значимости  и числе степеней свободы ). Проверка разности средних по -критерию Стьюдента не является единственным способом проверки зависимостей изменения показателей от времени, для этого разработан ряд критериев: использование повторных точек, корреляция рангов и др. [44].

5.2.2.2. Выбор формы кривой, описывающей

закономерности развития прогнозируемых показателей

Кривые роста, описывающие закономерности развития прогнозируемых показателей во времени, получают путем аналитического выравнивания динамических рядов.       Процесс выравнивания (т.е. подгонка выбранных функций к данным динамического ряда) состоит из двух основных этапов:

1. Выбор типа кривой, форма которой соответствует характеру изменения динамического ряда.

2. Определения числовых значений (оценивание) параметров кривой.

Вопрос о выборе типа кривой является основным при выравнивании ряда. Ошибка в решении этого вопроса оказывается более значимой по своим последствиям (особенно для прогнозирования), чем ошибка, связанная со статистическим оцениванием параметров. К выбору типа кривой можно подойти различными путями. Предварительно познакомимся с основными типами кривых, используемых при прогнозировании, и их основными свойствами.

Для выравнивания динамических рядов наиболее часто применяют такие относительно простые функции, как многочлены (полиномы), различного рода экспоненты и логистические кривые.

Многочлены имеют следующий вид:

первой степени            , (рис. 5.3,а);                       (5.6)

второй степени                         (рис.5.3,б);              (5.7)

третьей степени                        (рис.5.3,в)    (5.8)

-й степени                 .            (5.9)  

Здесь  - параметры многочленов;  - независимая переменная (время).

Многочлен первой степени (5.6) (см. рис.5.3,а) – на графике ему соответствует прямая линия – предполагает постоянство прироста ординат и поэтому применяется для процессов, равномерно развивающихся во времени.

Парабола второй степени (5.7) (см. рис.5.3,б) описывает движение с равномерным измерением приростов, причем приросты положительны для одной ветви параболы и отрицательны для другой. Парабола второй степени применима для описания процессов, характерной особенностью которых является равноускоренный рост или равноускоренное снижение уровня.

У полинома третьей степени (5.8) (см. рис.5.3,в) знак прироста ординат может изменяться один или два раза.

Самая простая экспоненциальная (показательная) кривая имеет вид (см. рис.5.3,г)

,                                     (5.10)

.                                     (5.11)

Более усложненным выриантом экспоненциальной кривой является логарифмическая порабола

.                                 (5.12)

Все рассмотренные выше кривые, соответствующие многочленам, не имеют асимптот, т.е. их рост ничем не ограничен. Теоретически ордината  может принимать любое значение.

Экспоненциальная кривая и логарифмическая парабола имеют асимптоты (например, у экспоненциальной кривой  при , если ).

В ряде случаев, когда процесс характеризуется насыщением, его описание имеет смысл лишь при помощи кривой, имеющей асимптоту, отличающуюся от нуля. Наиболее простым представителем семейства таких кривых является модифицированная экспонента

.                                (5.13)

Эта функция имеет горизонтальную асимптоту  (см. рис.5.3,д).

Достаточно широкое применение нашла -образная кривая (кривая Гомперца) (см. рис.5.3,е)

                                    (5.14)

и логистическая кривая (см. рис.5.3,ж)

,                               (5.15)

где  - некоторая функция от  (часто принимают ).

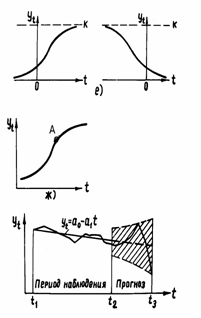
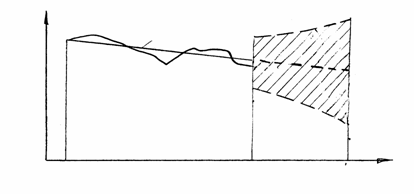
Экспоненциальные кривые роста хорошо описывают процессы, когда прирост зависит в основном от уже достигнутого уровня, при этом различного рода ограничения для роста не оказывают сколь-нибудь заметного влияния. Если же ограничивающий фактор все время воздействует, причем эффектность его влияния растет вместе с ростом достигнутого уровня, то хорошее описание этого процесса можно получить с помощью модифицированной экспоненты. Наконец, если ограничивающий фактор начинает влиять только после некоторого момента (точка перегиба), до которого процесс развивался, следуя близко к некоторому экспоненциальному закону, то наилучшее приближение дают -образные кривые.

Существует несколько практических подходов, которые позволяют удовлетворительно выбрать адекватную действительному ряду форму кривой.

Визуальный – выбор формы кривой на основе графического изображения динамического ряда – риск ошибки велик, дает приемлемые результаты при относительно простой конфигурации тенденции развития.

Метод последовательных разностей - используется в основном при подборе кривых, описываемых многочленами.

Метод, основанный на точности описания динамического ряда, исходя из величин выбранного критерия согласия (например, остаточная дисперсия).

Определение числовых значений параметров выбранного вида кривой решается известными статистическими методами обработки данных наблюдений.

5.2.2.3. Экстраполяция трендов

и доверительные интервалы прогноза

Экстраполяция – продление в будущее тенденции, наблюдавшейся в прошлом. Экстраполяция тенденций динамических рядов базируется на допущениях:

1. Развитие явления может быть с достаточным основанием охарактеризовано плавной траекторией – трендом.

2. Общие условия, определяющие тенденцию развития в прошлом, не претерпят существенных изменений в будущем.

При выполнении этих допущений процесс экстраполяции заключается в подстановке соответствующей величины периода упреждения в  формулу, описывающую тренд.

Экстраполяция, вообще говоря, дает точечную прогностическую оценку. Точное совпадение фактических данных и прогностических точечных оценок, полученных путем экстраполяции трендов, характеризующих тенденцию – явление маловероятное.

Соответствующая погрешность имеет следующие источники:

1. Выбор формы кривой, характеризующей тренд, содержит элементы субъективизма. Нет твердой основы того, что выбранная форма кривой является наилучшей для экстраполяции в данных конкретных условиях.

2. Оценивание параметров кривых производится на основе ограниченной совокупности наблюдений, каждое из которых содержит случайную компоненту. В силу этого параметрам кривой, а следовательно, и ее положению в пространстве свойственна некоторая неопределенность.

3. Тренд характеризует некоторый средний ряд на каждый момент времени. Отдельные наблюдения, как правило, отклонялись от него в прошлом. Естественно ожидать, что подобного рода отклонения будут происходить и в будущем.

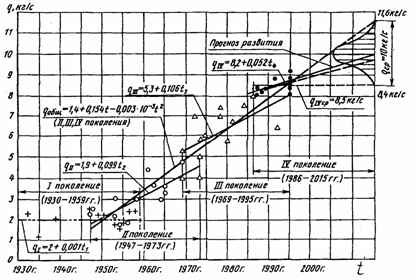
Рис. 5.4. Схема формирования точечного

и интервального экстраполяционного прогноза

Погрешность, связанная со вторым и третьим ее источником, может быть отражена в виде доверительного интервала прогноза (рис.5.4.). С помощью такого интервала точечный экстраполяционный прогноз преобразуется в интервальный.

Методы расчета доверительного интервала прогноза для основной группы трендов разработаны [44].

Формально доверительный интервал учитывает ту неопределенность, которая связана с ограниченностью числа наблюдений и соответствующей неточностью найденных оценок параметров кривой. Однако при этом остается в силе предположение о том, что прогнозируемый показатель равен средней, а доверительный интервал для прогностической оценки учитывает возможное (с заданной доверительной вероятностью) ее варьирование вокруг средней в будущем.

5.2.2.4. Пример статистического прогнозирования основных

показателей технического уровня зерноуборочных комбайнов

Парк комбайнов в нашей стране в 1956 г. насчитывал                 385,1 тыс. шт. (в основном с шириной захвата 4-4,9 м). Первое поколение отражает период становления и формирования конструкций комбайнов как в нашей стране, так и в других промышленно развитых странах Америки и Европы [36].

Ко II-му поколению следует отнести самоходные комбайны, обозначившиеся своим сравнительно несложным конструктивным оформлением - начальный этап их развития. В нашей стране эволюционный цикл развития II-го поколения комбайнов составил  лет, он начался в 1947 году и закончился в 1973 году.

Оборудование самоходных комбайнов кабинами ознаменовало появление III-го поколения машин. Это связано с существенным улучшением условий труда комбайнеров. Эволюционный цикл развития комбайнов III-го поколения составил 26 лет (начиная с 1969 года – «Сибиряк»).

Гидрообъемные передачи обозначили появление IV-го поколения комбайнов. Гидрообъемные передачи позволяют создавать высокопроизводительные комбайны с эксплуатационной массой 20 т и более, они обеспечивают бесступенчатую передачу мощности 75 кВт и более на привод МСУ, например, в аксиально-роторной модели М8570 фирмы Western (Канада). В России старт IV-му поколению дал «Дон-1500» в 1986 году. Этому поколению комбайнов предстоит дальнейшее развитие.

Рассмотрим инженерную методику применительно к прогнозированию развития поколений зерноуборочных комбайнов.

С учетом рекомендации [44] глубина прогноза развития                  IV-го поколения комбайнов принята равной средней величине из трех циклов – 26 лет (т.е. с 1986 по 2012 гг.). Однако следует учесть некоторую задержку развития комбайнов из-за кризисных явлений в экономике России и других стран. Поэтому глубина прогноза определена ориентировочно до 2015 года.

Универсальный показатель развития комбайнов – их эксплуатационная производительность. Однако присутствие в этом показателе элементов влияния эксплуатационных факторов заставляет обратиться к другому известному показателю или параметру – производительность за час чистого времени, которая практически независима от эксплуатационных факторов, но тесно связана с эксплуатационной производительностью, выражая ее потенциальные возможности.

Рис.5.5. Рост производительности за час чистого времени  по времени

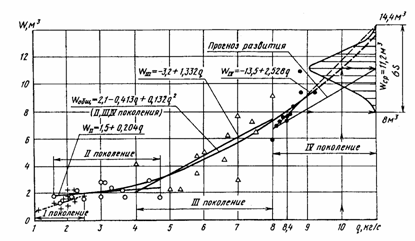
На рис.5.5 представлены графические и аналитические зависимости роста производительности  по годам для четырех поколений комбайнов, полученные методом наименьших квадратов. В отличие от прицепных машин самоходные по темпам роста оказались сходными между собой. Объединив в один массив точки II-го и III-го поколений, получим зависимость

.

Присоединив этому массиву имеющиеся на сегодня данные IV-го поколения, получим общую зависимость [18]

,               (5.16)

которая отражает слабо наметившуюся тенденцию отклонения                         от линейной зависимости в сторону снижения пропускной способности к 2015 году.

Следует отметить, что развитие комбайнов и поколений происходило в условиях интенсивного роста урожайности зерновых культур (табл.5.3), увеличения площадей убираемых массивов в связи с резким сокращением числа фермерских хозяйств, например, в США с 6,8 млн. в 1935 году до 2,2 млн. в 1986 году. Для уборки высокоурожайных и укрупненных массивов хлебов потребовались высокопроизводительные комбайны с высокой производительностью. Конструкции машин и достигнутый к тому времени уровень развития техники могли удовлетворить такие требования. В эти годы практически полностью были использованы сравнительно легко допустимые средства повышения производительности комбайнов: более чем вдвое увеличены ширина молотилок, длина клавишных соломотрясов, площади решет очисток.

Таблица 5.3

Урожайность пшеницы в некоторых промышленно развитых странах, ц/га

В предстоящий прогнозный период такого сочетания благоприятных условий развития комбайнов по производительности за час чистого времени, очевидно, не будет. К тому же добавятся органичения по увеличению производительности, а следовательно, и массы комбайнов, экологических требований, например, по допустимому уровню давления движителей комбайнов на почву. Одним словом, под влиянием объективных условий прогнозируемого периода средняя величина производительности моделей зернокомбайнов к 2015 году окажется ниже экстраполируемого значения 11,6 кг/с (см. рис.5.5), но она будет, несомненно, выше нижнего предела 8,4 кг/с, который уже достигнут сегодняшними моделями комбайнов IV-го поколения. Развитие последних продолжится до конца прогнозируемого периода.

Наиболее вероятная средняя производительность высокопроизводительных моделей к 2015 году составит 10 кг/с с распределением частот частных значений по кривой нормального распределения, что и отражено на рис.5.5.

С учетом неизбежных ошибок нашей выборки математическое ожидание или средняя величина генеральной совокупности производительности разместится в диапазоне

 кг/с,

где - значение критерия Стьюдента при вероятности 0,95;             - стандартная ошибка при минимально возможной выборке.

Важными параметрами комбайнов служат также объем бункера, мощность двигателя, масса машины. Исследования показали устойчивую корреляционную связь отмеченных параметров с производительностью по поколениям комбайнов, исключая первое поколение.

На рис.5.6. показаны графические линейные зависимости объема бункеров от производительности за час чистого времени по II-му,         III-му и известной части IV-го поколений комбайнов. Критерий Фишера по дисперсии аппроксимации показал, что объединенный массив точек отмеченных поколений лучше аппроксимируется не линейной, а параболической зависимостью [36]:

,                   (5.17)

которая действительна при 1 кг/с кг/с.

На рис.5.6 стрелками показан способ определения среднего объема бункера высокопроизводительных комбайнов 2015 года (11,2 м³), соответствующего к этому времени средней производительности 10 кг/с, и нижнего предела (8 м³), по которым построена кривая нормального распределения. Математическое ожидание объема бункеров найдет себе место в диапазоне

 м³

при вероятности 95%.

По аналогии с объемом бункеров построены графические зависимости мощности двигателя  и массы комбайна  от производительности за час чистого времени :

 кВт;

    при 1 кг/с кг/с;

 кВт;

     при 4 кг/с кг/с;

 кВт;

    при 8 кг/с кг/с.

Для отмеченных поколений получены общие зависимости [36]:

,                    (5.18)

.                (5.19)

В табл. 5.4 представлена сводка средних значений основных параметров наиболее произвольных моделей по поколениям.

Таблица 5.4

Средние значения основных параметров высокопроизводительных

комбайнов, относящихся к середине эволюционных циклов

(IV поколение – 2015 г.)

Поколение	Годы эволюционных периодов развития	Основные параметры
		Пропускная способность , кг/с	Объем бункера , м3	Мощность двигателя , кВт	Масса  , т
I II III IV (прогноз)	1930-1959 1947-1973 1969-1995 1986-2015	2,0 3,0 6,3 10±0,6	1,5 2,1 5,2 11,2±1,2	- 59 125 260±21	- 5,09 9,46 14,9±1

Инженерная методика прогнозирования развития комбайнов включает также методы и приемы получения опережающей информации, призванной дополнить и показать возможности достижения полученных экстраполяционными методами прогнозируемых значений параметров машин. С этой целью используются известные расчетные формулы, эмпирические зависимости, а также научно-техническая и патентная информация.

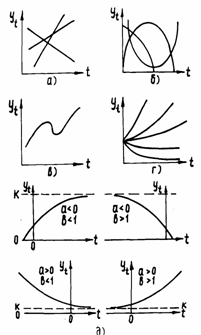
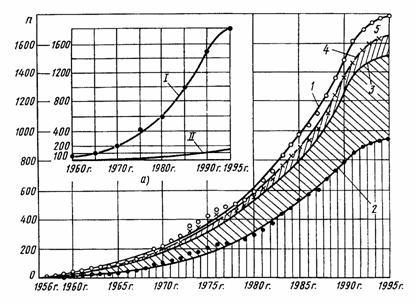
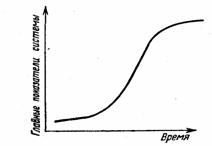
На рис.5.7 приведена обработанная с помощью морфологического классификатора патентная информация. Интегральная кривая 1 характеризует публикацию патентов и авторских свидетельств по зерноуборочным комбайнам с 1956 по 1995 гг. Судя по характеру кривой, скорость поступления патентной информации в нашей стране в 80-е годы была максимальной и не могла свидетельствовать о наступлении стагнации в развитии комбайнов.

Кривая 2 выделяет из общего массива патентную информацию, относящуюся к рабочим органам комбайнов, влияющих на повышение производительности: МСУ и домолачивающим устройствам, соломосепараторам и очисткам. Область между кривыми 3 и 2 выделяет изобретения, относящиеся в основном к жатвенной части. Эта область несколько дополнена приспособлениями для уборки незерновой части урожая. Область между кривыми 4 и 3 отражает поступления изобретений по бункерам, а также загрузочным и выгрузным устройствам к ним. Область 5 между кривыми 1 и 4 включает изобретения по автоматизации и гидрофикации комбайнов. На рис.5.7,  кривая I соответствует кривой 1 рис.5.7, а кривая II отражает интегральное поступление информации по некомбайновым способам уборки, а также по машинам и устройствам к ним.

Анализ кривых свидетельствует о достаточно большом и надежном заделе известных изобретений, направленных на повышение производительности комбайнов и совершенствование их конструкций. Значительное число изобретений по жатвенной части указывает на стремление изобретателей полнее использовать потенциальные возможности отечественных комбайнов в условиях работы на наших и зарубежных полях. Расширяющаяся с течением времени область 5 указывает на возрастающую роль автоматизации и гидрофикации в перспективном развитии комбайнов.

В результате проведенных исследований можно с уверенностью сказать, что на ближайшую обозримую перспективу 40-50 лет объективные условия гарантируют жизнедеятельность и развитие зерноуборочных машин.

Жизнь технической системы (как, впрочем, и других систем, например, биологических) можно изобразить в виде S-образной кривой (рис. 5.8), показывающей, как меняются во времени главные характеристики системы (мощность, производительность, скорость, число выпускаемых систем и т. д.) [47].

Рис. 5.8. Кривая жизненного цикла технической системы

 

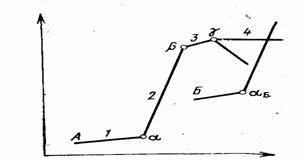
У разных технических систем эта кривая имеет свои индивидуальные особенности. Но всегда на ней есть характерные участки, которые схематически выделены на рис. 5.9. Определившись на каком участке развития в настоящее время находится система, можно предвидеть характер и темпы ее развития на будущее.

             

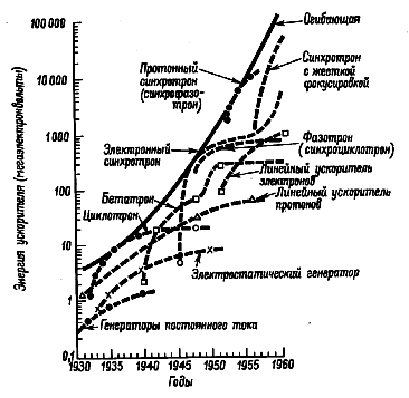
    Время

Рис. 5.9. Характерные участки кривой линии жизненного цикла: 1 - участок начального, медленного развития системы; 2. – участок быстрого развития системы, она быстро совершенствуется, начинается массовое ее применение; 3 – система стареет, темпы её развития замедляются; 4 – на данном участке техническая система либо деградирует, сменяясь принципиально другой системой Б, либо на долгое время сохраняет достигнутые показатели

Построение огибающих кривых позволяет прогнозировать основные показатели технических систем сходного назначения. Огибающие кривые описывают максимально достигнутые значения функциональных характеристик вне зависимости от конкретных конструктивных особенностей тех или иных технических средств.

Огибающая кривая, представленная на рис. 5.10, отражает общую тенденцию развития технических систем с одинаковыми техническими функциями. Проекция огибающей в будущее содержит минимальную вероятность совершения крупной ошибки, поскольку такая операция предполагает, что в будущем сохранится прежний темп появления новых изобретений и не предвидится необъяснимого разрыва между прошлым и будущем.

Рис. 5.10 Огибающая кривая и темпы роста энергии

отдельных конструкций ускорителей частиц

Хотя огибающие кривые, на самом деле, в будущем могут не продолжаться так, как в прошлом, полезно предположить, что другой ход кривых будет плавным и прогрессирующим. Основанием для такого предположения является тот факт, что как только темп изменений устанавливается, кривая приобретет своеобразную инерцию, т.е. кривая является самовоспроизводящейся.

Секрет достоверности прогнозов заключается в отыскании такого метода экстраполяции, при котором принимается во внимание непрерывность процесса появления изобретений и не требуется предвидение деталей будущего изобретения.

Методами экстраполяции при прогнозе функциональных характеристик машин и оборудования, можно достичь глубины 7 лет. При пониженных требованиях к точности – 10 лет. Однако для планирования НИР и выбора направления поисковых разработок необходимо получать оценку функциональных характеристик исследуемых систем  на глубину в 20 и более лет. Для достижения необходимой глубины прогнозов используют, как правило, методы экспертных оценок, мирясь с присущим этим методам субъективизмом экспертов, или специальные приёмы получения ориентировочных оценок,  опирающихся на комбинацию методов экстраполяции с методами статистики, информатики и наукометрии. Практика прогнозирования показывает, что такие методы в меньшей степени подвержены субъективизму и , в конечном итоге, дают более точные оценки прогнозируемых характеристик.

Ниже приводятся примеры выбора показателей функциональных характеристик, использования статистики, информатики, наукометрии для прогнозирования на глубину 20 и более лет.

 При прогнозах на такую глубину, при сопоставлении вариантов исполнения технических систем, как правило, используют безразмерные показатели, относительной функциональной эффективности, относительной ресурсной эффективности и относительной финансовой эффективности.

Для прогноза значений этих показателей, характеризующих состояние вариантов системы на глубину 20 и более лет, разработана специальная процедура [46, 47]. Показатели эффективности для вариантов конструктивного исполнения рассчитываются как произведение базового показателя, характеризующего достижимый уровень,   и двух критериев подобия, характеризующих особенности условий работы прогнозируемой системы и конструктивные особенности её реализации. Для расчёта значений базовых  показателей эффективности и критериев подобия была создана специальная база данных FINCOST, включающая информацию о 1040 схемных решениях сельхозмашин и их конструктивных исполнениях. Кроме полей, описывающих количественные оценки эффективности, состав, последовательность функций известных машин, в базу введены поля, содержащее вербальные описания (на естественном языке) вариантов конструктивного исполнения функций машины.

Разработанная методика и её информационное обеспечение позволяют надёжно прогнозировать функциональные показатели и существующих,  и вновь создаваемых конструкций.

Этот метод прогнозирования функциональных параметров разработан для  приближённой, ориентировочной оценки этих показателей на глубину в 15 -20 лет [46, 47].  В основе этого метода лежит представление о разных темпах развития параметров системы в разные периоды её жизненного цикла.

За время жизненного цикла системы (60 лет) характеристики его функционирования возрастают в среднем в 4 раза. За первую треть жизненного цикла функциональные параметры прирастают на 66%, за вторую треть – прирастают на 33% и за третью – всего на 1%. В период «молодости» конструктивного исполнения такой системы (первая треть цикла) динамика патентной активности положительна. В период «зрелости» конструктивного исполнения (вторая треть) динамика патентной активности близка к 0. В период «старости» конструктивного исполнения (последняя треть) динамика патентной активности отрицательна.

Сопоставление приведенных выше данных позволяет построить приближённую зависимость для оценки прироста функциональных показателей конструктивных исполнений функций за время необходимой глубины прогноза.

,                   (5.20)

где  и  - соответственно прогнозируемый и исходный показатели функциональной эффективности варианта технической системы; - необходимая глубина прогноза; - коэффициент прироста функциональной эффективности варианта технической системы.

Если прогнозируемая система находится в первой трети своего развития, то патентная активность, оцененная за 10 – 15 лет в отношении конструктивного исполнения такой системы, будет возрастать. Коэффициент прироста функциональной эффективности этого варианта технической системы будет 0,132 (соответствует приросту на 66% за          20 лет от общего, четырёхкратного). Если прогнозируемая система находится во второй трети своего развития, то патентная активность за               10-15 лет в отношении конструктивного исполнения такой системы в среднем стабильна. Коэффициент прироста функциональной эффективности такого варианта технической системы будет 0,064 (соответствует приросту на 33% за 20 лет). Если прогнозируемая система находится в последней трети своего развития, то патентная активность в отношении конструктивного исполнения такой системы снижается. Коэффициент прироста функциональной эффективности этого варианта технической системы будет 0,002 (соответствует приросту на 1% за 20 лет).                                                

Использование этого метода позволило прогнозировать функциональные показатели вариантов сельхозмашин, использующих различные конструктивные исполнения носителей функций.

Для прогнозов направления развития оборудования нами разработан метод долгосрочного прогнозирования схемных решений оборудования, основанный на нечётких качественно-количественных оценках [46, 47].

Основу метода составляет система моделей направленного синтеза структуры оборудования, синтеза и ранжирования конструктивных решений для каждой из выделенных схем, прогноза спроса на оборудование.

Для направленного синтеза структуры сельхозмашин были выделены функции, состав и последовательность которых формируют их структуру. Эти функции были сгруппированы в множество функций, которые преобразуют исходное состояние обрабатываемого продукта, которые, изменяя положение продукта, обеспечивают работу основным функциям, множество функций которые обеспечивают энергией основные и вспомогательные функции, которые обеспечивают управление режимами  работы носителей функций машины и которые обеспечивают заданное размещение и удержание в пространстве носителей функций машины. Структура машины представлена в виде объединения расплывчатых множеств основных и вспомогательных функций.

Базовое понятие теории нечётких (расплывчатых) множеств, оценка степени соответствия заданного элемента  множеству использовано нами для отбора из множества функций при синтезе структуры только тех, оценка степени соответствия которых выше заданной, пороговой. В свою очередь, степень соответствия для функции оценивалась как композиция  представлений потенциальных покупателей о структуре будущей машины, истории производства и продаж машин с такими функциями, оценки общественной потребности на функцию по патентной активности.

 Для прогнозирования спроса на оборудование была разработана процедура на основе метода построения сценариев. Работу процедур метода прогнозирования направления развития сельхозмашин поддерживают специализированные компьютерные базы данных.

Оценка эффекта от прогнозирования направления развития (по степени снижения информационной энтропии, по К.Э. Шеннону) показывает, что вероятность получения конкурентоспособного изделия увеличивается в 140–150 раз.