Примеры алгоритмов расчета валов на статическую прочность
Исходными данными являются силы, действующие в зацеплении – Ft, Fr, Fx, крутящие моменты – Т, расстояние между опорами (подшипниками) – ℓ, их координаты относительно левого конца вала. Исходные данные получены в результате расчета передач и из компоновки редуктора.
Расчет входного вала редуктора с прямозубой цилиндрической передачей и шкивом. (рис. 14)
Дано: Ft2, Fr2, Т3, ℓ, b – расстояние от правой опоры до центра муфты, x1– координата расположения зубчатого колеса относительно левой опоры.
Обозначения: левая опора – Л, правая опора – П.
Определяем опорные реакции, Н.
От силы Ft2 в вертикальной плоскости.
Составляем сумму моментов, действующих в вертикальной плоскости относительно левой опоры.
От действия окружной силы Ft2.
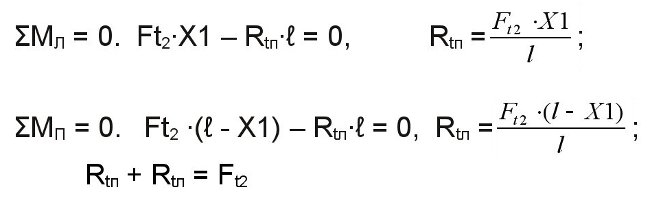
Составляем сумму моментов, действующих в горизонтальной плоскости относительно левой опоры.
От действия радиальных сил Fr2.
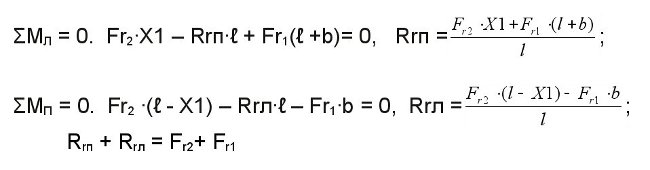
Реакции опор – суммарные
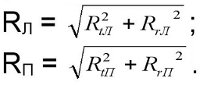
Изгибающие моменты в опасном сечении под зубчатым колесом;
Вертикальная плоскость от силы Ft2.
Mи (Ft2) = RtЛ · Х1,
Горизонтальная плоскость от сил Fr1 и Fr2.
Mи(Fr1) = Fr1 · b
Mи(Fr2) = Rrл · Х1.
Суммарный изгибающий момент в наиболее нагруженном сечении – под зубчатым колесом
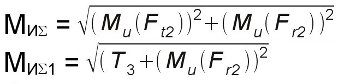
Приведенный момент
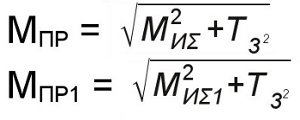
Материал для изготовления валов:
Сталь 20, НВ≥200; σв = 500; σт= 260; σ-1= 136; τ-1 = 70; Ψ1=0; Ψ2=0
Диаметры вала в опасных сечениях:
Диаметр конца вала под шкив – d2
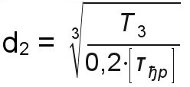 (мм), ввиду наличия шпоночного паза увеличивается на 10% и округляется в большую сторону по ГОСТ6636 - 69
Диаметр вала под подшипник – d1
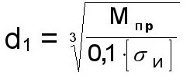 (мм), полученное значение округляем в большую сторону по посадочному диаметру подшипника – d
Диаметр вала под зубчатое колесо – d
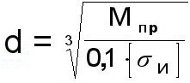 (мм), ввиду наличия шпоночного паза увеличивается на 10% и округляется в большую сторону до ближайшего стандартного размера согласно ГОСТ 6636-69 "Нормальные линейные размеры".
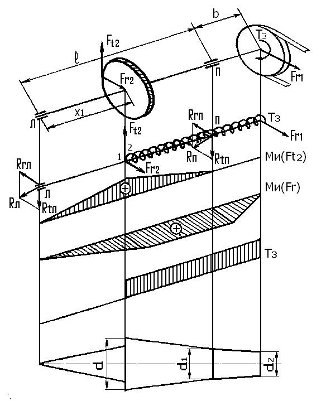
Рис. 14 (оригинал)
Расчет входного (выходного) вала редуктора с косозубой цилиндрической передачей. (рис.15)
Дано: Ft1, Fr1, Т1, ℓ, а – расстояние от центра муфты до правой опоры, x1– координата расположения зубчатого колеса относительно левой опоры.
Обозначения: левая опора – Л, правая опора – П.
Определяем опорные реакции, Н.
От силы Ft1 в вертикальной плоскости.
Составляем сумму моментов, действующих в вертикальной плоскости относительно левой опоры.
От действия окружной силы Ft1.
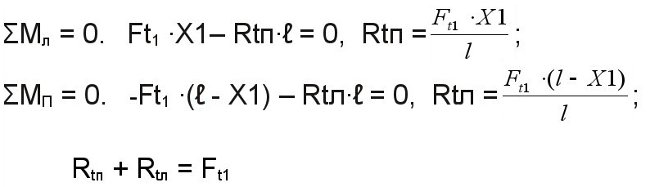
От действия радиальной силы Fr1 в горизонтальной плоскости.
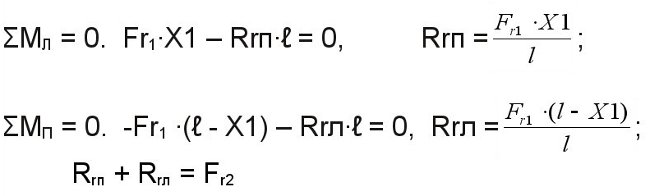
От действия осевой силы Fх1 в горизонтальной плоскости.
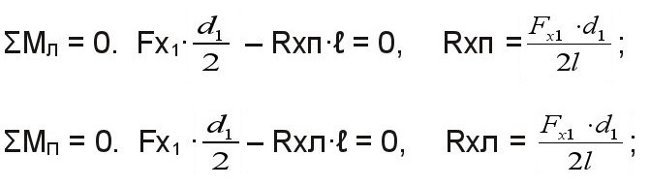
Реакции опор – суммарные
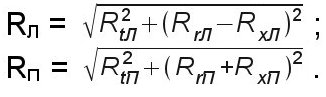
Изгибающие моменты в опасном сечении под зубчатым колесом;
Вертикальная плоскость (от силы Ft1)
Mи (Ft1) = RtЛ · Х1,
Горизонтальная плоскость – суммируем изгибающие моменты (от сил Fr1 и Fx1).
Слева от сечения
Mиг Л = (Rrл – Rхл)·Х1
Справа от сечения
Mиг П = (Rrп + Rхп)·(ℓ - Х1).
Суммарный изгибающий момент в наиболее нагруженном сечении – под зубчатым колесом, рассчитываем с учетом наибольших изгибающих моментов в горизонтальной и вертикальной плоскостях.
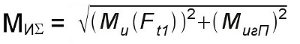
Приведенный момент
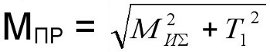
Материал для изготовления валов:
Сталь 20, НВ≥200; σв=500; σт=260; σ-1=136; τ-1=70.
Диаметры вала в опасных сечениях:
Диаметр конца вала под муфту – d
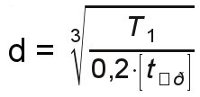
(мм), ввиду наличия шпоночного паза увеличивается на 10% и округляется в большую сторону по посадочному диаметру муфты.
Диаметр вала под зубчатое колесо – d1
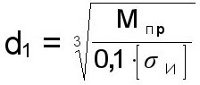
ввиду наличия шпоночного паза увеличивается на 10% и округляется в большую сторону до ближайшего стандартного размера согласно ГОСТ 6636-69 "Нормальные линейные размеры"
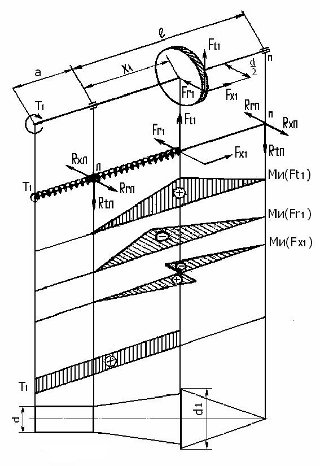
Рис. 15 (оригинал)
Расчет ведущего вала с коническим прямозубым колесом на консоли (Рис.16).
Исходные данные: T1;
Нагрузка от зубчатого колеса:
Ft1; Fr1; Fx1.
Нагрузка от муфты Т1.
Определение опорных реакций в горизонтальной плоскости.
От действия осевой силы Fx1.
МиFx =Fx·0,5·dm1
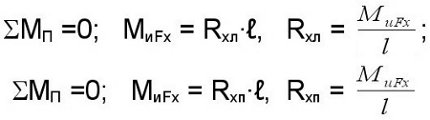
От действия радиальной силы Fr1
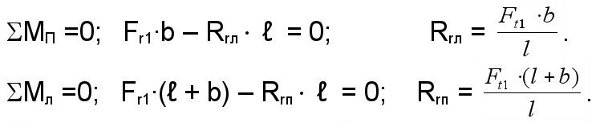
Определение опорных реакций в вертикальной плоскости.
От действия окружной силы Ft1.
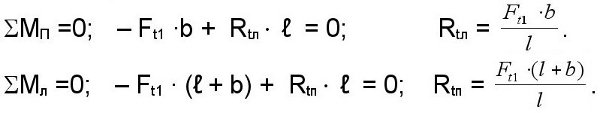
Реакции опор – суммарные.
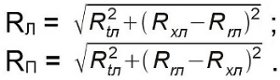
Изгибающий момент в опасном сечении (на правой опоре)
Суммарный изгибающий момент в наиболее нагруженном сечении - 3, справа
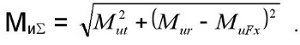
Приведенный момент
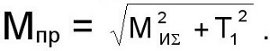
Материал для изготовления валов:
Сталь 20, НВ≥200; σв=500; σт=260; σ-1=136; τ-1=70; Диаметры вала в опасных сечениях
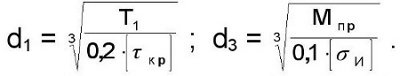
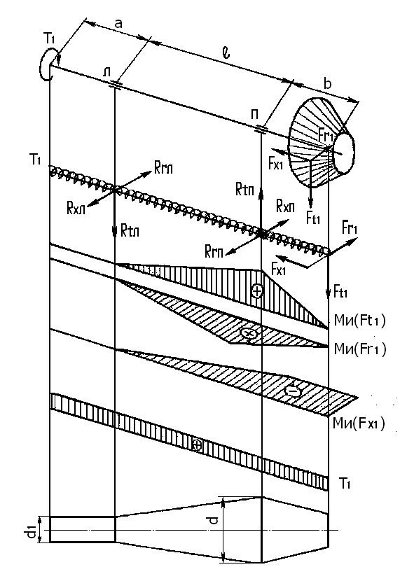
Рис. 16 (оригинал)
Расчет промежуточного вала редуктора (Рис.17).
Исходные данные:
Передача цилиндрическая прямозубая: T2 ; Ft2; Fr2.
Передача цилиндрическая косозубая: -T2 ; Ft1; Fr1; FХ1
Из компоновки редуктора, расстояние между опорами L ;
Координата прямозубого колеса относительно левой опоры – Х1
Координата косозубого колеса относительно левой опоры – Х2
Определение опорных реакций в вертикальной плоскости.
От действия окружных сил Ft1 и Ft2.
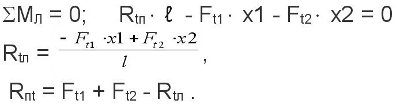
От действия радиальных сил Fr1 и Fr2.
Составляем сумму моментов относительно левой опоры в горизонтальной плоскости.
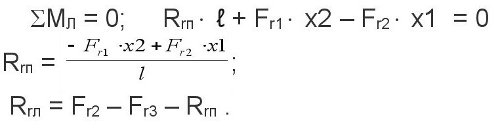
От действия осевой силы Fx1 в горизонтальной плоскости.
Составляем сумму моментов относительно левой и правой опор.
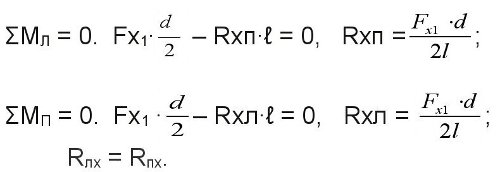
Суммарные реакции опор (радиальные нагрузки на подшипники)
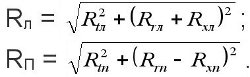
Изгибающие моменты в сечении 2 (слева от сечения);
Mи(Ft) = Rtл × Х2;
Mи(Fr) = Rrл × Х2;
Mи(Fx) = Rxл × Х2.
Изгибающие моменты в сечении 3 (справа от сечения);
Mи(Ft) = Rtп × (ℓ – Х1);
Mи(Fr) = Rrп × (ℓ – Х1);
Mи(Fx) = Rxп × (ℓ – Х1).
Суммарный изгибающий момент в сечении - 2, слева
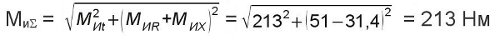
Суммарный изгибающий момент в сечении - 3, справа
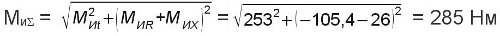
Приведенный момент в сечении - 2
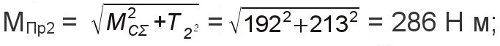
Приведенный момент в сечении - 3
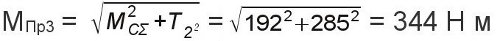
Диаметры вала в опасных сечениях
Материал для изготовления валов:
Сталь 45 НВ≥200; σв=560; σт=280; σ-1=250; τ-1=150; Ψ1=0; Ψ2=0
где -
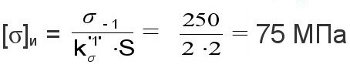
– допускаемое напряжение изгиба;
klσ= 2 – ориентировочное значение коэффициента концентрации
S = 2…2,5 – ориентировочное значение коэффициента запаса прочности.
Принимаем S = 1,7
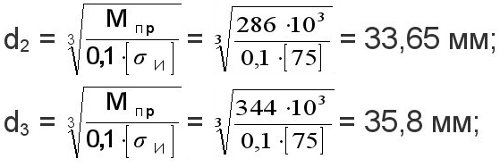
Учитывая ослабление вала шпонками и наличие стандартных размеров подшипников,
принимаем d1=40 мм; d2=42 мм; d3=45 мм; d4=40 мм.
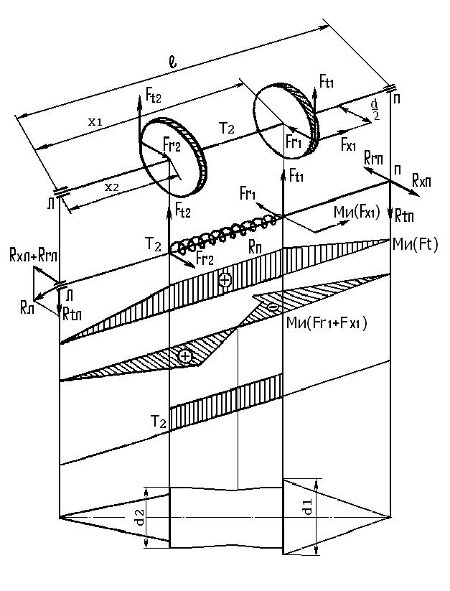
Рис. 17 (оригинал)
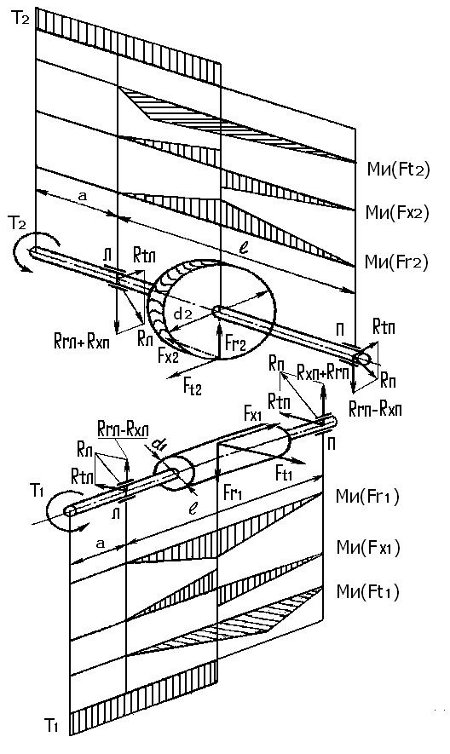
Рис. 18 (оригинал)
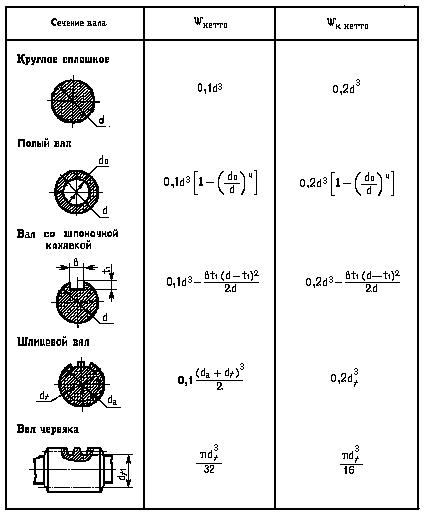
Расчет валов червячного редуктора проводится по методике расчета вала с цилиндрическим косозубым колесом, расположенным симметрично относительно опор. (Рис. 18)
| 
