Рассмотрим понятия нечеткой и лингвистической переменных, которые используются при описании объектов и явлений, а также организации нечеткого логического вывода.

Нечеткая переменная характеризуется тройкой <, X, A>, где

           - наименование переменной,

          X - универсальное множество (область определения ),

          A - нечеткое множество на X, описывающее ограничения (т.е. (x)) на значения нечеткой переменной .

Лингвистической переменной⁴⁶ называется набор  <, T, X, G, M>,

где                - наименование лингвистической переменной;

          Т - множество ее значений (терм-множество), представляющих собой наименования нечетких переменных, областью определения каждой из которых является множество X;

Множество T называется базовым терм-множеством лингвистической переменной;

          G - синтаксическая процедура, позволяющая оперировать элементами терм-множества T;

          М - семантическая процедура, позволяющая превратить каждое новое значение лингвистической переменной, образуемое процедурой G, в нечеткую переменную, т.е. сформировать соответствующее нечеткое множество.

Замечание. Чтобы избежать большого количества символов

·        символ  используют как для названия самой переменной, так и для всех ее значений;

·        пользуются одним и тем же символом для обозначения нечеткого множества и его названия, например терм "молодой", являющийся значением лингвистической переменной =  "возраст", одновременно есть и нечеткое множество М("молодой").

Присвоение нескольких значений символам предполагает, что контекст позволяет разрешить возможные неопределенности.

Пример 18. Пусть эксперт определяет толщину выпускаемого изделия с помощью понятий "малая толщина", "средняя толщина" и "большая толщина", при этом минимальная толщина равна 10 мм, а максимальная - 80 мм. Формализация такого описания может быть проведена с помощью следующей лингвистической переменной <, T, X, G, M>, где

                - толщина изделия;

               T - {"малая толщина", "средняя толщина", "большая толщина"};

               X - [10, 80];

               G - процедура образования новых термов с помощью связок "и", "или" и модификаторов типа "очень", "не", "слегка" и др. Например: "малая или средняя толщина", "очень малая толщина" и др.;

               М - процедура задания на X = [10, 80] нечетких подмножеств А₁="малая толщина", А₂= "средняя толщина", А₃="большая толщина", а также нечетких множеств для термов из G(T) в соответствии с правилами трансляции нечетких связок и модификаторов "и", "или", "не", "очень", "слегка" и др.

Замечание. Наряду с рассмотренными выше базовыми значениями лингвистической переменной "толщина" (Т={"малая толщина", "средняя толщина", "большая толщина"}) возможны значения, зависящие от области определения Х. В данном случае значения лингвистической переменной "толщина изделия" могут быть определены как "около 20 мм", "около 50 мм", "около 70 мм", т.е. в виде нечетких чисел.

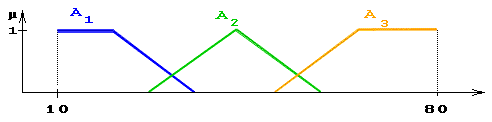
Рис.1.3. Пример графического отображения нечетких переменных

Нечеткие числа⁴⁸ это нечеткие переменные, определенные на числовой оси, т.е. нечеткое число определяется как нечеткое множество А на множестве действительных чисел R с функцией принадлежности (x)[0,1], где x - действительное число, т.е. xR.

Нечеткими высказываниями⁴⁵ называются высказывания следующего вида:

        1. Высказывание < есть '>, где  - наименование лингвистической переменной, ' - ее значение, которому соответствует нечеткое множество на универсальном множестве Х. Например высказывание <давление большое> предполагает, что лингвистической переменной "давление" придается значение "большое", для которого на универсальном множестве Х переменной "давление" определено соответствующее данному значению  "большое" нечеткое множество.

        2. Высказывание < есть m'>, где m - модификатор, которому соответствуют слова "ОЧЕНЬ", "БОЛЕЕ ИЛИ МЕНЕЕ", "МНОГО БОЛЬШЕ" и др.

          Например: <давление очень большое>, <скорость много больше средней> и др.

        3. Составные высказывания, образованные из высказываний видов 1. и 2. и союзов "И", "ИЛИ", "ЕСЛИ.., ТО...", "ЕСЛИ.., ТО.., ИНАЧЕ".

Логико-лингвистические методы описания систем основаны на том, что поведение исследуемой системы описывается на естественном (или близком к естественному) языке в терминах  лингвистических переменных.

     Входные и выходные параметры системы рассматриваются как лингвистические переменные, а качественное описание процесса задается совокупностью высказываний следующего вида:

     L₁ : если <A₁ > то <B₁ >,

     L₂ : если <A₂ > то <B₂ >,

     ....................

     L_k : если <A_k > то <B_k >,

где <A_i>, i=1, 2, .., k - составные нечеткие высказывания, определенные на значениях входных лингвистических переменных, а <B_i>, i = 1, 2, .., k - высказывания, определенные на значениях выходных лингвистических переменных.

Совокупность импликаций {L₁, L₂, ..., L_k} отражает функциональную взаимосвязь входных и выходных переменных и является основой построения нечеткого отношения XRY, заданного на произведении XY универсальных множеств входных и выходных переменных. Если на множестве X задано нечеткое множество A, то композиционное правило вывода B=AR определяет на Y нечеткое множество B с функцией принадлежности

(y) =((x)&(x,y))

Таким образом, композиционное правило вывода, в этом случае задает, закон функционирования нечеткой модели системы.

Пусть F – полное множество, охватывающее всю проблемную область. Нечеткое множество h множества F определяется через функцию принадлежности m_h(f), где f – элемент множества F. Эта функция отображает элементы f множества F на множество чисел в отрезке [0, 1], которые указывают степень принадлежности каждого элемента нечеткому множеству h.

Если F = {f₁,f₂,f₃,…,f_n}, то нечеткое множество h можно представить в следующем виде:

h = m_h(f₁)/f₁+m_h(f₂)/f₂+…+m_h(f_n)/f_n =

            В данном случае знак «+» означает совокупность элементов множества (знаменатель) с их принадлежностью (числитель).

            Пусть полное множество F – это значение температуры в интервале от 0 до 100 градусов. С использованием нечетких множеств можно определить такие качественные понятия (нечеткие переменные), как «низкая», «средняя», «высокая» (температура). Например:

            h₁=низкая=m_низкая(F)=1/0+1/10+0,5/20+0,1/30;

            h₂=средняя=m_{средняя}(F)=0,3/30+0,5/40+1/50+0,5/60;

            h₃=высокая=m_{высокая}(F)=0,1/50+0,3/60+0,5/70+0,8/80+1.90.

В приведенных выражениях члены с принадлежностью 0 не записаны.

При выполнении нечетких выводов необходимо использовать нечеткие отношения. Нечетким отношением R между некоторой проблемной областью (полным множеством F₁) и другой областью (полным множеством F₂) называется нечеткое множество прямого декартова произведения F₁´F₂, определяемое следующим образом:

,

где F₁={f₁₁, f₁₂,…, f_1l,}, F₂={f₂₁, f₂₂,…, f_2m,}.

            Пусть имеется правило типа «ЕСЛИ h₁, ТО h₂», где h₁ и h₂ – нечеткие множества, определенные как: ; , тогда нечеткое отношение можно задать следующим образом:

.

            Например, зададим качественное понятие «большое давление» на полном множестве G={g₁, g₂,…,g_m} значений давления в интервале от1 до 100 атмосфер.

k₁ = «большое» = m_{большое}(G) = 0,5/70 + 0,8/80 + 1/90.

            Если имеется правило вида⁴⁹: «ЕСЛИ температура высокая, ТО давление большое» («ЕСЛИ f высокая, ТО g большое» или h₃=>k₁), то можно построить нечеткое отношение, содержащее только значения принадлежности (f_i, g_j), следующим образом:

 В случае наличия цепочки правил в процессе нечеткого вывода используется свертка нечетких отношений. Обычно используется свертка вида «max-min», которая задается следующим образом. Пусть R – нечеткое отношение из области F в область G, а S – нечеткое отношение из области G в область полного множества W. Тогда нечеткое отношение из области F в область W определяется как свертка:

.

Например, пусть W множество балльных оценок, отражающих степень опасности W={1,2,3,4,5} и на этом множестве определено понятие «чрезвычайная»:

                        n₁=m_{чрезвычайная}(W) = 0,2/4+0,9/5.

            Тогда, если имеется цепочка нечетких правил:

            «ЕСЛИ температура высокая, ТО давление большое»,

            «ЕСЛИ давление большое, ТО опасность чрезвычайная».

            (h₃ => k₁ – отношение R, k₁ => n₁ – отношение S),

то результирующее отношение, реализующее правило h₃ => n₁, получается следующим образом:

                              70     80    90                4        5                  4       5

Полученное отношение позволяет осуществлять нечеткие выводы с использованием цепочки нечетких правил. Например, если определить для значение температуры нечеткое понятие «около 70» как h¢=m_{около 70}(F) = 0,5/60+1/70+0,5/80, то с использованием отношения Z можно получить нечеткий вывод относительно возможной опасности, также выполнив операцию свертки:

Вывод относительно степени опасности w¢=0,2/4+0,5/5 можно интерпретировать как «достаточно опасно».

            На рис.1.4 изображен пример реализации нечеткого правила с использованием реляционного отношения. Отношение Q включает в свой состав компоненты правила вида «ЕСЛИ-ТО». В качестве составных частей правила используются нечеткие множества (лингвистические переменные), определенные на полных множествах значений факторов F₁, F₂ и результата R₁. Для задания нечетких понятий используются отношения F₁, F₂, R₁. Число доменов в этих отношениях обычно небольшое, так как в практических приложениях наиболее удобно использовать трапециевидную функцию принадлежности, требующую задания четырех значений. На рис.1.5 изображен пример задания такой функции. Незаданные значения функции принадлежности могут быть вычислены, но это требует использования специальных процедур.

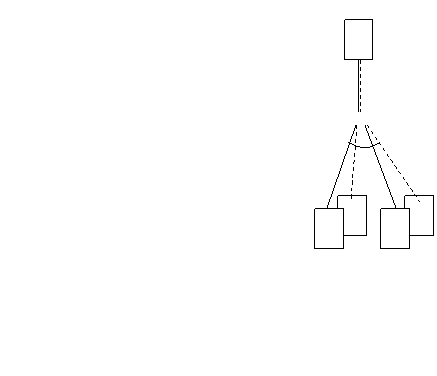
В примере на рис.1.4 считается, что в отношениях представлены принадлежности для всех используемых при выводе элементов полных множеств. Процесс вывода в подобной системе разбивается на два этапа. На первом этапе вывод аналогичен выводу в обычной продукционной системе. После того, как найдено правило, удовлетворяющее нечетким утверждениям и дающее качественный результат, пользователю предоставляется возможность задать нечеткие факты и получить нечеткий вывод. Для примера на рис.2 эта процедура должна включать следующие шаги (например, для первого правила):

-         для лингвистических переменных h₁₁, h₁₂, r₁ находится их представление в соответствующих отношениях F₁, F₂, R₁;

-         строятся нечеткие отношения T₁= h₁₁´r₁ и T₂= h₂₁´r₁;

-         пользователю предоставляется возможность задать нечеткие факты h¢₁₁ и h¢₂₁, после этого с использованием операций свертки находятся два нечетких результата r¢₁₁= h¢₁₁° T₁ и r¢₁₂= h¢₂₁° T₂;

-         конечный нечеткий результат r¢ находится с использованием операции пересечения .

В случае необходимости использования цепочки правил, реализуется свертка соответствующих отношений. Разрешение конфликтов в системе осуществляется с использованием подходов, принятых в продукционных системах.

Пусть A, B, M, R - нечеткие понятия определенные на соответствующих полных множествах  ( в  случае оценивания знаний в  нечеткой среде, это могут быть  качественные определения уровня знаний  заданные на соответствующем полном множестве, определяемом выбранной шкалой для оценивания).

Рис.1.5. Задание нечеткого множества трапециевидного типа.

Понятие A определено на полном множестве V={1, 2, 3, 4}:

A= 0/1 + 0.5/2 + 0.5/3 + 0.1/4.

Понятие B определено на полном множестве U={10, 20, 30}:

B= 0.5/10 + 0.5/20 + 1/30.

Понятие M определено на полном множестве Z={1, 2, 3, 4, 5}:

M= 0.1/1 + 0.2/2 + 0.5/3 + 0.9/4 + 1/5.

Понятие R определено на полном множестве W={100, 200, 300}:

R= 0/100 + 0.7/200 + 0.9/300.

Пусть введенные нечеткие понятия объединены системой продукционных  правил:

(1) ЕСЛИ (A или B) ТО M;

(2) ЕСЛИ M ТО R.

Элементарной продукции (продукция с одной предпосылкой) в теории нечетких множеств соответствует понятие отношения:

 если

Логические выражения И, ИЛИ представляются операциями пересечения и объединения , соответственно, для нечетких понятий входящих в продукцию.

В заданном примере ситуация осложнена тем, что в продукцию (1) входят нечеткие предпосылки определенные на различных полных множествах. Учитывая данный факт, невозможно выполнить преобразования следующего вида:

ЕСЛИ (A или B) ТО M ® ЕСЛИ F ТО M, где F= A È B, которое возможно только  в случае, когда А и В определены на одном и том же полном множестве.

В данном случае необходимо осуществить разбиение сложной продукции на составные компоненты, а операцию объединения выполнить для значений промежуточных результатов.

Пусть на вход заданной системы нечетких продукций поступают сведущие нечеткие факты:

А'= 0/1 + 0.8/2 + 0.8/3 + 0.2/4;

B'= 0.3/10 + 0.3/20 + 0.7/30.

Тогда процесс  логического вывода может быть выполнен в следующем порядке:

1. Получить нечеткое отношение, соответствующее продукции:

ЕСЛИ А ТО М₁, где М₁ нечеткое понятие М₁= М.

--> z_k

2. Получить нечеткое отношение, соответствующее продукции:

ЕСЛИ В ТО М₂, где М₂ нечеткое понятие М₂=М.

--> z_k

3. Для каждой из вспомогательных продукций (отношений): ЕСЛИ А ТО М₁; ЕСЛИ В ТО М₂, необходимо определить нечеткие результаты М₁' и М₂', получаемые  при условии, что используются нечеткие факты А' и B'.

Операция разрешения (вывода) для элементарной продукции в случае нечеткого правила реализуется через операцию свертки, вида:

M₁' = A'M1; M₂' = B'M2,

где , (отношение RS, это отображение из u в w).

Для рассматриваемого примера:

;

.

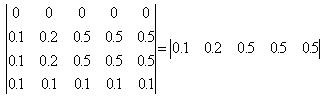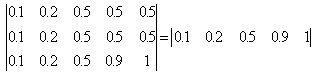4. Получив выражения для  M₁' и M₂' имеется возможность получить значение  М', как М'=M₁'ÈM₂', так как M₁' и M₂' определены на одном полном множестве Z: .

5. Для элементарной продукции (2), так же необходимо получить отношение: REZ= Z ° W.

6. В результате выполненных преобразований имеется возможность получить нечеткий результат для заданной системы продукций и предпосылок, как R'=M'REZ:

,

т.е. R'= 0/100 + 0.7/200 + 0.9/300.

Рассмотренный пример логического  вывода в системе нечетких продукций демонстрирует основные принципы построения обработки знаний в интеллектуальных системах.