 |
|
Выберете лекцию |
|
|
Пример 1. Машина, увеличивающая данное число на единицу — машина «1». В начале работы головка воспринимает заполненную ячейку (ячейку, содержащую символ 1), и внутренняя память машины находится в состоянии q1. В процессе работы машина находит справа пустую ячейку, печатает в ней единицу и останавливается. В результате работы машинное слово 01xq11y00 (где 1n означает последовательность из п единиц) преобразуется в слово 01x+yq010.
Преобразование, осуществляемое машиной в результате выполнения программы,
будем обозначать стрелкой
![]() .
В данном случае имеем
.
В данном случае имеем
01xq11y00
![]() 01x+yq0100.
01x+yq0100.
Запишем совокупность команд, составляющих данную программу:
q11 ® q11П — после выполнения у раз этой команды машина придет в состояние 01x+yq100;
q10 ® q01C — после выполнения этой команды машина приходит в состояние 01x+yq010.
Пример работы машины при х=2, y=4 приведен в табл. 4.1. Состояние машины предоставлено в таблице словом, записанным на ленте с символом внутренней памяти, расположенным над воспринимаемой ячейкой.
Таблица 4.1.
|
Номер такта |
Состояние машины |
|
0
1
2
3
4
5 |
q1
0 1 1 1 1 1 1 0 0 q1 0 1 1 1 1 1 1 0 0 q1 0 1 1 1 1 1 1 0 0 q1 0 1 1 1 1 1 1 0 0 q1 0 1 1 1 1 1 1 0 0 q1 0 1 1 1 1 1 1 1 0 |
Машина выполняет программу и в том случае, если х=у=0; при этом слово 0q100 преобразуется в слово 0q010.
Программу машины можно представить в виде таблицы, содержащей необходимые команды. Программа рассмотренной машины представлена табл. 4.2., где а — символ обозреваемой ячейки, q — символ состояния внутренней памяти.
Таблица 4.2.
| q \ a | 0 | 1 |
| q1 | q01C | q11П |
Пример 2. Машина, уменьшающая данное число на единицу — машина
«-1». Эта машина осуществляет преобразование
01xq11y0![]() 01x+y-2q01000
(y>0)
01x+y-2q01000
(y>0)
Воспринимая в исходном состоянии заполненную ячейку, машина находит правый край данного массива единиц, стирает единицу и останавливается напротив самой правой из оставшихся единиц. Дополнительное условие, машина «отказывается» работать, если в начальном состоянии она воспринимает незаполненную ячейку.
Команды, осуществляющие данную программу:
q11 ® q21П — после выполнения команды получаем слово
01x+1q21y-10;
q21 ® q21П —после выполнения (у—I) раз этой команды машин приходит в состояние
01x+yq20;
q20 ® q30Л —это дает слово
01x+y-1q310;
q31 ® q00Л — после выполнения этой команды имеем заключительное слово
01x+y-2q0100.
Программа .данной машины приведена в табл. 4.3.
Таблица 4.3.
| Q \ a | 0 | 1 |
| Q1 | - | Q21П |
| Q2 | Q30Л | Q21П |
| Q3 | - | Q00Л |
В программе отсутствуют команды, начинающиеся словами q10 и q30. Но ситуация q30 вообще не встречается при работе машины, а ситуация q10 встречается только в тех случаях, когда данная программа не применима (в этих случаях внутренняя память машины не приходит в заключительное состояние, оставаясь в состоянии q1).
Пример 3. Машина, сдвигающая головку вправо, на следующий массив единиц — машина «С+». Необходимо осуществить преобразование
01xq11y0z1w![]() 01x+y0z1w-1q0
10 (y
01x+y0z1w-1q0
10 (y![]() 0,
z
0,
z![]() 1,
w
1,
w![]() 1)
1)
(0z здесь означает последовательность из z нулей). Машина находит следующий справа массив единиц и останавливается, воспринимая самую правую заполненную ячейку.
Программа содержит команды:
q11 ® q11П (через у тактов команда дает слово 01x+yq10z1v0);
q10 ® q20П,
q20 ® q20П (выполнение этих команд приводит к слову 01x+y0z q21v0);
q21 ® q31П,
q31 ® q31П (получается слово 01x+y0z1vq30);
q30 ® q00Л (получается заключительное слово). Программа приведена в табл. 4.4.
Таблица 4.4.
| Q \ a | 0 | 1 |
| Q1 | Q20П | Q11П |
| Q2 | Q20П | Q31П |
| Q3 | Q00Л | Q31П |
Если исходное машинное слово имеет вид 01xq11y00… , то машина продолжает работать «вечно», пристраивая справа пустые ячейки и не приходя в заключительное состояние; таким образом, данная программа не применима к слову 01xq11y00… .
Будем рассматривать также машины Тьюринга, внутренняя память которых имеет не одно, а несколько заключительных состоянии.
Пример 4. Машина, проверяющая истинность равенства х = 0,— машина «Пр». В исходном положении машина воспринимает самую правую заполненную ячейку массива из х+1 единиц, изображающего на ленте число х. Если слева от этой ячейки — пустая ячейка, то по окончании работы машины ее внутренняя память приходит в состояние q01; если слева — заполненная ячейка, внутренняя память приходит в состояние q02:
01xq11
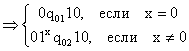
Работа машины осуществляется в соответствии со следующей программой (справа от команд будем писать слово, получающееся в результате применения данной команды):
q11![]() q21Л:
01x-1q2110
(или q2010
при x=0),
q21Л:
01x-1q2110
(или q2010
при x=0),
q21![]() q021П:
01xq0210
(или q20
q021П:
01xq0210
(или q20![]() q010П:
0q0110).
q010П:
0q0110).
Программа машины представлена в табл. 4.5.
Таблица 4.5.
| Q \ a | 0 | 1 |
| Q1 | - | Q21Л |
| Q2 | Q010П | Q021П |
Приведем далее без пояснений программы нескольких простых машин.
Пример 5. Машина «С-», сдвигающая головку влево на следующий массив единиц:
01x+10y1zq11w![]() 01xq010y1z+w0,
01xq010y1z+w0,
либо, если z = v = 0:
01x+10yq10![]() 01xq010y0
01xq010y0
(в последнем случае, в частности, может быть у = 0).
Программа машины приведена в табл. 4.6.
Таблица 4.6.
| Q \ a | 0 | 1 |
| Q1 | Q20Л | Q11Л |
| Q2 | Q20Л | Q01C |
Пример 6. Машина «H», печатающая число 0:
01xq11y000![]() 01x+y0q010
(x
01x+y0q010
(x![]() 0,
y>0);
0,
y>0);
в частном случае может быть
01xq11y001z0![]() 01x+yq01z+10
01x+yq01z+10
Программа машины приведена в табл. 4.7.
Таблица 4.7.
| Q \ a | 0 | 1 |
| Q1 | - | Q21П |
| Q2 | Q30П | Q21П |
| Q3 | Q01C | - |
Пример
7. Машина «Ст», стирающая данный массив единиц:
![]()
Программа машины приведена в табл. 4.8.
Таблица 4.8.
| Q \ a | 0 | 1 |
| Q1 | Q20Л | Q10Л |
| Q2 | Q20Л | Q01C |
Пример
8. Машина «У», удаляющая все нули (кроме одного), расположенные между
данным массивом единиц и ближайшим слева.
![]()
Построим сначала программу для осуществления следующего цикла:
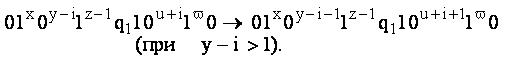
Как и прежде, слева будем писать команды, а справа — машинные слова, получающиеся в результате применения этих команд столько раз, сколько они применимы:
![]()
q11
® q11Л
— после выполнения этой команды z раз получим слово
Далее,
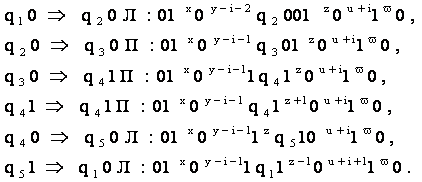
После выполнения (у—1) циклов
исходное машинное слово преобразуется в следующее:
![]()
Применение к полученному слову
z раз команды q11
® q11Л
и команды q10
® q20Л
дает:
![]()
Введем команду
![]()
Далее имеется команда:
![]()
Вводим затем команды

Программа машины «У» приведена в табл. 4.9.
Таблица 4.9.
| Q \ a | 0 | 1 |
| Q1 | Q20Л | Q11Л |
| Q2 | Q30П | Q21П |
| Q3 | Q41П | Q61П |
| Q4 | Q50Л | Q41П |
| Q5 | - | Q10Л |
| Q6 | Q00Л | Q61П |