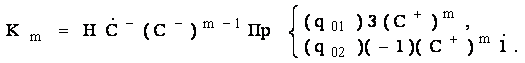Наряду с опе­рацией композиции машин при синтезе программ используется операция итерации. Рассмотрим машину T₁, имеющую k заключительных состояний внутренней

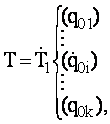
памяти q₀₁,

..., q_0k. Отождествим одно из этих состояний (например, q_0i) с начальным состоянием машины. Операция отождествления одного из заключительных состояний внутренней памяти машины с ее исходным состоянием называется операцией итерации¹⁸. Машина Т, получаемая в резуль­тате итерации машины Т₁, обозначается через точки над символами, которые указывают на отождествление i-го заключительного состояния с начальным состоянием машины T₁. В результате итерации получаем машину, внутренняя память которой во время работы совершает один или несколько замкнутых циклов. Если в процессе выполнения программы внутренняя память машины должна прийти в состояние q_0i, то она возвращается в начальное состояние, и машина вновь начинает работать. Работа машины продолжается до тех пор, пока ее внутренняя память не придет в какое-либо из остальных заключительных состояний. Если машина Т₁ имеет лишь одно заключительное состояние, то в результате итерации получаем машину, вообще не имеющую заключительных состояний. Такая машина работает по замкнутому циклу бесконечно или останавливается, если в процессе работы получено машинное слово, к которому программа машины неприменима.
Итерация может объединяться с композицией машин. Например, в машине

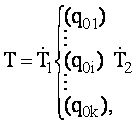
после того, как внутренняя память приходит в состояние q_0i, выполняется программа Т₂, после чего внутренняя память приходит в начальное состояние, и вновь выполняется программа T₁.

Использование операций композиции и итерации позволяет построить из простых машин более сложные; при этом сложные машины описываются компактным выражением.

Пример 12. Используя машины, введенные в примерах 1—9, с помощью операции композиции и итерации построим машину К_m осуществляющую копирование m-го с правого края массива единиц:

Рассмотрим случай, когда m=1:

Представим машину K₁ с помощью композиции и итерации введенных выше машин. Найдем сначала машину, осуществляющую при x—i > 0 циклическое преобразование:

Преобразуя слово

по программе машины «—1», получим

Далее применим программы «С⁺» и «1»:

Воспользовавшись машиной «С^-», получим

Таким образом, нужное преобразование осуществляет композиция (-1)С⁺1С^-. Для того чтобы замкнуть цикл, перед выполнением программы (-1)С⁺1С^- нужно осуществить проверку равенства x-i=0. Для этого воспользуемся машиной «Пр». Если x-i>0, то внутренняя память приходит в состояние q₀₂», и далее выполняется программа (-1)С⁺1С^-.
Машина, осуществляющая нужное циклическое преобразование, быть описана выражением

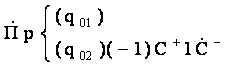
Если эта машина начинает работать при i=l, то через (х—1) циклов получим слово 0q10^x1^x0. Для получения нужного машинного слова 01^x01^x-1q10 применим далее машины:

З: 01^x-1q101^x0,

C⁺: 01^x01^x-1q₀10.

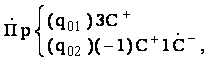
В результате мы построили машину преобразующую слово 01^x-1q10100 … в нужное слово 01^x01^x-1q₀10.

Осталось построить машину, осуществляющую преобразование

т.е. машину, преобразующую исходное слово в слово, к которому применимо наше циклическое преобразование. Для этого используем машины:

H: 01^x0q100 … ,

C^-: 01^x-1q10100 … .

Окончательно получаем

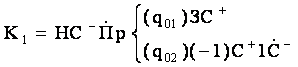
или

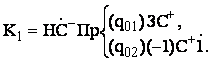
Последнее выражение несколько короче предыдущего, но описывает ту же самую программу, т. е. количество тактов при осуществлении программы и в том, и в другом случае одинаково.

Можно найти, что в общем случае (при т > 1)