При синтезе машин Тьюринга, осуществляющих требуемые преобразования машинных слов, существенную роль играет понятие композиции машин¹⁷. Пусть заданы машины Тьюринга Р и Q, имеющие общий внешний алфавит {a₀, a₁, ..., a_m} и внутренние алфавиты соответственно {q₀, q₁, ..., q_n} и {q₀, q’₁, ..., q’_v}. Пусть машина осуществляет преобразование машинного слова А в слово В, а машина Q - преобразование слова В в слово С. Требуется построить машину R, которая осуществляла бы преобразование слова А в слово С. Для осуществления требуемого преобразования необходимо, чтобы, машина R сначала выполнила до конца преобразования по программе машины Р, а затем провела преобразования в соответствии с программой машины Q. Очевидно, что программу машины R можно получить, объединив программы машин Р и Q; причем в программе машины Р стоп-символ q₀ заменим символом q_n+1; оставив неизменными остальные символы внутреннего алфавита, а в программе машины Q каждый из символов q'_i (i=1, 2, ..., w) заменим символом q_i+n, оставив неизменным символ q₀. Тогда внутренняя память машины R после выполнения преобразований по программе машины Р приходит в состояние q_n+1, после чего машина R начинает работать по программе машины Q. Машина R с внешним алфавитом {а_о, a₁, ..., a_m}, внутренним алфавитом {q₀, q₁, ..., q_n+w} и программой, полученной из программ машин Р и Q указанным образом, называется композицией машин Р и Q, или произведением машины Р на машину Q (обозначается: R=PQ).

Пример 10. Используя понятие композиции машин Тьюринга, построим программу машины Т, сдвигающей головку вправо, на следующий массив единиц, изображающий некоторое число v,

                                                                          Таблица 4.10

увеличивающей это число на единицу и останавливающейся:

 Очевидно, что данная машина может быть представлена композицией машин «С⁺»  и «1»: T=C⁺1

Для получения таблицы команд машины Т заменим символ q₀ в таблице 4.4 и символ q₁ в таблице 4.2 символом q₄. Полученная программа машин Т представлена в табл. 4.10.

Понятие композиции дает общий метод синтеза машин, который значительно облегчает построение сложных программ. Существенным является то, что ряд ма­шин, последовательно выполняющих свои программы, всегда можно заменить одной машиной, являющейся их композицией.

С. помощью непосредственной проверки можно убе­диться, что произведение машин Тьюринга—некоммута­тивная операция, т. е. в общем случае PQ ¹ QP. Произ­ведение одинаковых машин Тьюринга называется возведением в степень. Для возведения в степень используется обычное обозначение Рⁿ. Например, п-й степенью ма­шины С⁺ является машина, сдвигающая головку вправо на (п+1)-й массив единиц, считая от исходного:

При построении композиций машин Тьюринга, име­ющих более одного заключительного состояния, необходимо указать, какое из заключительных состояний отождествляется с начальным состоянием следующей  машины.

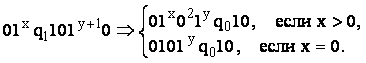
Пример 11. Построить программу машины, которая, воспринимая в исходном состоянии крайнюю правую ячейку записи данного числа x, уменьшает число х на единицу и сдвигает головку вправо, если х>0, и просто сдвигает головку вправо, если х=0:

Требуемая программа может быть представлена в виде композиции машин Пр, -1, С⁺:

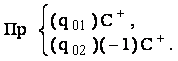
Команды, входящие в данную программу, получим, заменив в программе машины «Пр»

символ q01 на q3 символ,

символ q₀₂ на q₆ символ;

в программе машины «С⁺»

символ q_i на символ q_i+2 (i=1, 2, 3);

в программе машины «-1»

символ q_j на символ q_j+5 (j=1, 2, 3),

символ q₀ на символ q₃

и объединив полученные программы.