Рассмотрим теперь, как с помощью машины Тьюринга осуществляется вычисление значений какой-либо функции f(x₁, ..., x_п), Для того чтобы определить, что означает вычисление функции на машине Тьюринга, необходимо определить некоторую стандартную форму записи исходных данных и полученного результата и стандартное положение считывающей головки в начале и в конце вычисления. Будем записывать число х совокупностью из x+l единиц. Будем говорить, что два числа расположены рядом (подряд) на ленте, если между запи­сями чисел имеется одна пустая ячейка. Оставим пустой самую левую ячейку ленты и запишем далее подряд числа x₁, ..., x_п. Будем говорить, что считывающая головка воспринимает систему чисел (x₁, ..., x_п) в стандартном положении, если эти числа записаны на ленте подряд и головка воспринимает самую правую заполненную ячейку в представлении последнего из чисел x_n.

Пусть в начале работы машина воспринимает в стандартном положении систему (x₁, ..., x_п). Будем говорить, что машина вычисляет частичную функцию f(x₁, ..., x_п), если

1) для всех систем чисел (x₁, ..., x_п), для которых функция f(x₁, ..., x_п) определена, по окончании работы машина воспринимает в стандартном положении систему чисел (x₁, ..., x_п, f(x₁, ..., x_п)) и внутренняя память находится в заключительном состоянии, т. е.

2) для всех систем чисел (x₁, ..., x_п), для которых функция f не определена, машина, начав работать, не приходит в заключительное состояние.

Функция называется вычислимой на машине Тьюринга, если существует машина Тьюринга, вычисляющая эту функцию.

Теорема.  Класс функций, вычислимых на машинах Тьюринга¹⁹, совпадает с классом частично-рекурсивных функций.

Эта теорема доказывает эквивалентность уточнений понятия алгоритма с помощью машин Тьюринга и с помощью теории рекурсивных функций. Рассмотрим кратко процесс доказательства одного из утверждений теоремы: частично-рекурсивные функции вычислимы на машинах Тьюринга.

В соответствии с определением частично-рекурсивной функции для доказательства достаточно показать, что простейшие функции s, С¹₀, Iⁿ_m и функции, возникающие с помощью операторов суперпозиции, примитивной рекурсии и минимизации, вычислимы на машинах Тьюринга. Для примера, построим машины, вычисляющие некоторые функции с помощью операций композиции и итерации.

1) Машина, вычисляющая функцию следования s(x)=x+1:

Эта машина может быть описана выражением s=K₁l.

2) Машина, вычисляющая функцию С¹₀(x)=0:

Это преобразование осуществляется машиной С¹₀=Н.

3) Машина, вычисляющая функцию тождества Iⁿ_m(x₁, ..., x_п)=x_m:

Преобразование осуществляется машиной Iⁿ_m = К_n-m+1.  

4) Машина, вычисляющая функцию, возникающую с помощью оператора суперпозиции. Рассмотрим подробно лишь случай одноместных функций g(x)=F(f(x)). Необходимо построить машину, осуществляющую преобразование,

Для доказательства предположим, что существуют машины, вычисляющие функции f и F; обозначим их соответственно через Т_f и Т_F. В результате последовательного выполне­ния программ имеем:

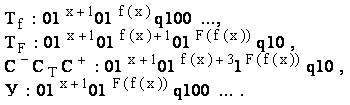
Следовательно, нужная машина описывается композицией