::Логика высказываний::

Математическая логика рассматривает языки, позволяющие сформировать символьное представление (систему формальных обозначений) для рассуждений, встречающихся как в математике, так и при описании реальных ситуаций.

Изучение математической логики начинается с логики или исчисления высказываний.

Исчисление высказываний (ИВ) изучает предложения которые могут быть или истинными, или ложными. Рассмотрим три истинных утверждения:

1). «За четверть часа до своей смерти он был еще жив».

2). « Если верно, что когда идет дождь, то дорога мокрая, тогда справедливо если дорога сухая, то дождя нет».

Чтобы убедится в правильности достаточно поменять смысл слов т.е. это предложение является истинной языка. Чтобы принять 2-е предложение достаточно поменять смысл некоторых слов, а также знать, что фрагменты фразы: «Идет дождь» и «дорога мокрая» являются высказываниями, которые могут быть или истинными, или ложными. Второе предложение останется истинным если заменить 2 высказывания другими. Третье предложение является истинной языка, т.е. выражает некоторый факт.

Рассмотрим словарь исчисления, который состоит из бесконечно счетного множества высказываний, обозначенных строчными буквами из логических связок. Высказывания представляют собой предложения которые могут быть или истинными, или ложными. Синтаксис логики высказываний безотносителен к ее связи с фразами естественного языка. Словарь исчисления позволяет строить сложные или составные высказывания из исходных, соединяя последние связками. Правила построения описывает те выражения, которые являются объектами языка, фразами, т.о. фразы- составное высказывание построенное по определенным правилам:

2). Если X и Y формулы, то

X, X&Y, X

Y, X®Y, X«Y являются формулами.

3). Формулы однозначно получаются с помощью двух предыдущих правил.

Круглые скобки позволяют указать порядок в котором применяются правила построения. Употребление скобок является следствием древовидности логических формул. Корневой узел дерева является главной связкой формулы.

Для определения истинности составных формул можно, так же как в булевой алгебре, использовать таблицы истинности. При этом каждое высказывание, или иначе атом, имеют одно из двух истинностных значений: «истинна» (И или 1) и «ложь» - (Л или 0). Истинностное значение любой составной формулы можно вычислить, исходя из истинностных значений атомов. Приписывание истинностных значений¹⁶ формулам называется интерпретацией формулы.

В качестве примера рассмотрим истинностную таблицу⁶ формул X&Y, X

Y, X®Y.

X	Y	X&Y	XY	X®Y
0	0	0	0	1
0	1	0	1	1
1	0	0	1	0
1	1	1	1	1

Пусть дана формула G=X&Y. Атомами этой формулы являются X и Y. Формула G истинна, если атомам X и Y приписаны значения 1(И) и 1(И) соответственно. Приписывание⁷ истинностных значений {1, 1} атомам {X, Y} соответственно называется интерпретацией формулы G. Так как каждому из атомов можно приписать 1 или 0, то имеется 2²=4 интерпретаций формулы G. Таблица, в которой указаны истинностные значения формулы G при всевозможных истинностных значениях атомов, называется истинностной таблицей формулы G.

Говорят, что формула G истинна при любой интерпретации, тогда и только тогда, когда G получает значение И в этой интерпретации; в противном случае говорят, что G ложна при этой интерпретации. Если формула G¹² истинна при всех ее интерпретациях, то такую формулу называют общезначимой формулой или тавтологией. Формула G необщезначима тогда и только тогда, когда она не является общезначимой.

Формула является противоречивой¹⁷ тогда и только тогда, когда она ложна при всех своих интерпретациях. Говорят, что формула непротиворечива (или выполнима), тогда и только тогда, когда она не является противоречивой.

Для преобразования формул¹⁸ используются эквивалентные формулы. Две формулы F и G эквивалентны тогда и только тогда, когда истинностные значения F и G совпадают при каждой интерпретации F и G. К таким формулам относятся коммуникативные, ассоциативные, дистрибутивные законы, а также законы де Моргана. Пусть 1 обозначает формулу, которая всегда истинна, а 0 - формулу, которая всегда ложна. Тогда мы имеем набор эквивалентных формул, приведенных в таблице 1, где F, H, G - формулы.

Важными понятиями в логике являются понятия нормальных форм. Так, формула F⁸ находится в конъюнктивной форме, тогда и только тогда, когда F имеет вид F₁&F₂&...&F_n, n

1, где каждая из F₁, F₂,..., F_n - дизъюнкция атомов или их отрицаний. Формула F⁹ находится в дизъюнктивной форме, тогда и только тогда, когда F имеет вид F₁F₂...F_n, n

1, где каждая из F₁, F₂,..., F_n - конъюнкция атомов или их отрицаний.

Всякая формула может быть преобразована, на основе эквивалентных формул, в нормальную форму.

Пример 1. Пусть необходимо получить дизъюнктивную нормальную форму для формулы (P

Шаг 1. Используя таблицу 1 преобразуем исходную формулу в эквивалентную, т.е. (P

Q. На этом шаге мы дважды использовали правило 2.

Шаг 2. Применяя к полученной формуле правило 16 из таблицы 1 получим:

Шаг 3. Используя правило 15 будем иметь требуемую нормальную форму: (

(

Q))

Q=(

P&Q)

Пример 2. Получить конъюнктивную нормальную форму для формулы

Шаг 1. Как и в предыдущем примере вначале используем правило 2. В результате получим: (P& (Q

R))

(P& (

R))

Шаг 2. К полученной, в результате преобразований, формуле применим правило 17:

Шаг 5. Для получения конъюнктивной нормальной формы применим правило 7:

При использовании рассуждений часто нужно решить, следует ли одно утверждение из нескольких других. Это приводит к понятию «логического следствия». Пусть даны формулы F₁, F₂,..., F_n и формула G. Говорят, что G есть логическое следствие формул F₁, F₂,..., F_n_,, тогда и только тогда, когда для всякой интерпретации I, в которой F₁&F₂&...&F_n истинна, G также истинна.

На практике для вывода логических следствий из некоторого множества формул (посылок) используют следующие две теоремы, которые приводим без доказательства.

Теорема 1¹⁰. Пусть даны формулы F₁, F₂,..., F_n и формула G. Тогда G есть логическое следствие F₁, F₂,..., F_n_,, тогда и только тогда, когда формула ((F₁&F₂&...&F_n)

G) общезначима.

Теорема 2¹¹. Пусть даны формулы F₁, F₂,..., F_n и формула G. Тогда G есть логическое следствие F₁, F₂,..., F_n_,, тогда и только тогда, когда формула (F₁&F₂&...&F_n&

G) противоречива.

Если формула G является логическим следствием формул F₁, F₂,…, F_n, то формула ((F₁...F_n)

G) называется теоремой, а G - заключением теоремы.

Для того, чтобы показать, что G является логическим следствием F=F₁, F₂,..., F_n можно использовать несколько методов²⁵.

1. Метод истинностных таблиц. В этом случае необходимо показать, что G истинна в каждой интерпретации F.

2. На основе теоремы 1. Это делается путем расширения истинностной таблицы, позволяющей определить истинностные значения формулы F

3. На основе теоремы 2, доказывая общезначимость формулы F

G путем преобразования ее в конъюнктивную нормальную форму.

4. На основе теоремы 2. В этом случае надо показать, что формула F&

G противоречива. Это можно сделать либо используя истинностную таблицу, либо посредством преобразования F&

G в дизъюнктивную нормальную форму.

Пример 3. Рассмотрим формулы F₁:(P

Q); F₂:

Q, G:

P. Покажем различными способами, что G является логическим следствием F₁ и F₂.

Способ 1. На основе истинностной таблицы⁶ необходимо показать, что G истинна в каждой интерпретации формулы (P

Q)&

Q. Построим истинностную таблицу для этой формулы и формулы G.

P	Q	PQ	Q	(PQ)&Q	P
1	1	1	0	0	0
1	0	0	1	0	0
0	1	1	0	0	1
0	0	1	1	1	1

Из таблицы видно, что существует только одна истинностная интерпретация⁷ для формулы (P

Q)&

Q, а именно {

Q}. Заключение G истинно в этой интерпретации. Отсюда заключаем, что

P есть логическое следствие F₁ и F₂.

Способ 2. Расширим предыдущую таблицу посредством вычисления истинностных значений формулы ((P

Q)&

P	Q	PQ	Q	(PQ)&Q	P	((PQ)&Q)P
1	1	1	0	0	0	1
1	0	0	1	0	0	1
0	1	1	0	0	1	1
0	0	1	1	1	1	1

Данная таблица показывает, что формула ((P

Q)&

P истинна при всех интерпретациях, и следовательно она общезначима. Согласно теореме 1¹⁰

P есть логическое следствие F₁ и F₂.

Способ 3. Необходимо доказать общезначимость формулы ((P

Q)&

P путем преобразования ее в конъюнктивную нормальную форму⁸.

Шаг 1. В соответствии с правилом 2 таблицы 1⁵ получим:

Шаг 3. В соответствии с правилом 19 таблицы 1 преобразуем последнюю формулу:

Шаг 4. Преобразуем последнюю формулу по правилу 9:

Шаг 6. Используя правила 5 и 18 таблицы 1 будем иметь:

Шаг 7. В соответствии с правилом 11 таблицы 1 получим: Q

1=1.

Отсюда следует, что формула ((P

Q)&

P общезначима.

Способ 4. Докажем противоречивость формулы (P

Q)&

Q&P, в соответствии с теоремой 2¹¹, путем преобразования ее в дизъюнктивную нормальную форму⁹.

Шаг 3. Применяя правило 19 таблицы 1 окончательно получим:

В логике атом или отрицание атома называют литерой. Часто для удобства множество литер рассматривается как синоним дизъюнкта. Например, P

R={P, Q,

R}. Когда дизъюнкт не содержит никаких литер, его называют пустым дизъюнктом. Пустой дизъюнкт будем обозначать через

. Для проверки невыполнимости множества дизъюнктов используется следующий метод. Пусть S - множество дизъюнктов. Тогда возможно применение следующих правил.

1. Правило тавтологии¹². Вычеркиваются все тавтологичные дизъюнкты из S. Оставшееся множество S¹ невыполнимо тогда и только тогда, когда и S невыполнимо.

2. Правило однолитерных дизъюнктов. Если существует единичный дизъюнкт L в S, то S¹ получается из S вычеркиванием тех дизъюнктов в S, которые содержат L. Если S¹ пусто, то S выполнимо. В противном случае строят множество S², выбрасывая из S¹ вхождения

L. S² невыполнимо тогда и только тогда, когда и S невыполнимо. Если

L - единичный дизъюнкт, то при вычеркивании

L он превратится в

3. Правило чистых литер. Литера в основном дизъюнкте из S называется чистой в S тогда и только тогда, когда литера

L не появится ни в каком основном дизъюнкте из S. Если литера L чистая в S, то вычеркиваются все основные дизъюнкты, содержащие L. Оставшееся множество S^’ невыполнимо тогда и только тогда, когда и S невыполнимо.

4. Правило расщепления. Если множество S представимо в виде (A₁L)&...&(A_mL)&...&(B₁

L)&...&(B_n

L)&R, где A_i, B_i, R свободны от L и

L, то получим множества расщепления S₁=A₁&...&A_m и S₂=B₁&...B_n&R. При этом S невыполнимо тогда и только тогда, когда (S₁S₂) невыполнимо.

Мощным правилом вывода в логике является метод резолюций. Основная идея метода состоит в том, чтобы проверить, содержит ли множество предложений S пустой дизъюнкт. Если S содержит пустой дизъюнкт, то S невыполнимо. Если же S не содержит пустой дизъюнкт, то осуществляется попытка его получения из S. В логике высказываний данный метод имеет более простой вид.

Пусть даны дизъюнкты: C₁: P и C₂:

PQ. Используя правило однолитерных дизъюнктов, из C₁ и C₂ можно получить дизъюнкт C₃: Q. Правило однолитерных необходимо для того, чтобы определить имеется ли контрарная пара литеры (например, P) в C₁ и литеры (например,

P) в C₂. Если такая пара имеется, то она вычеркивается из C₁ и C₂ для того, чтобы получить дизъюнкт C₃, который есть Q. Контрарность означает следующее: если A - атом, то две литеры A и

A контрарны друг другу, а множество { A,

A } называется контрарной парой.

Обобщением данного правило является правило резолюций: для любых двух дизъюнктов C₁ и C₂, если существует литера L₁ в C₁, которая контрарна литере L₂ в C₂, то, вычеркнув L₁ и L₂ из C₁ и C₂ соответственно, построим дизъюнкцию оставшихся дизъюнктов. Построенный дизъюнкт называется резольвентой C₁ и C₂. Важным свойством резольвенты является то, что любая резольвента двух дизъюнктов C₁ и C₂ есть логическое следствие C₁ и C₂. Суть вывода на основе резольвенты заключается в получении пустого дизъюнкта из S.

Пример 4. Рассмотрим следующие дизъюнкты: C₁: PR и C₂:

PQ.

Дизъюнкт C₁имеет литеру P, которая контрарна литере

P в C₂. Следовательно, вычеркивая P и

P из C₁ и C₂ соответственно и составляя дизъюнкцию оставшихся дизъюнктов R и Q получим резольвенту RQ.

Любая резольвента двух дизъюнктов C₂и C₂ есть логической следствие этих дизъюнктов. Пусть S - множество дизъюнктов. Резолюцонным выводом C из S называется такая конечная последовательность C₁, C₂,…C_k дизъюнктов, что каждый C_i или принадлежит S или является резольвентой дизъюнктов, предшествующих C_i, причем C_k=C. Вывод

из S называется опровержением или доказательством невыполнимости S.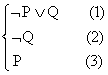

Из (1) и (2) получим резольвенту

P - (4). Из (4) и (3) получаем резольвенту

, которая и есть логической следствие S. Следовательно, S невыполнимо.

Таким образом исходными элементами в логике высказываний являются атомы. Из атомов можно построить формулы, которые используются для того, чтобы выразить различные предложения и умозаключения. В простой логике атом представляет повествовательное предложение, которое может быть или истинно или ложно, но не то и другое вместе. Атом рассматривается как единое целое. Его структура и состав не анализируются. Однако есть много предложений, которые не могут быть рассмотрены таким простым способом. Например, рассмотрим следующее умозаключение:

Приведенное рассуждение интуитивно корректно. Однако если мы введем обозначения:

то R не есть логическое следствие Р и Q в рамках логики высказываний. Это происходит потому, что в логике высказываний структура Р, Q и R не используется. Рассмотрим логику первого порядка, которая по сравнению с логикой высказываний имеет еще три логических понятия (называемые термами, предикатами и кванторами). Большая часть повседневного и математического языка может быть формализована логикой первого порядка.

Так же, как и в логике высказываний, сначала определим атомы логики первого порядка. Прежде чем дать формальное определение атома, рассмотрим несколько примеров. Допустим, что мы желаем представить утверждение «х больше 5». Сначала определим предикат БОЛЬШЕ(х, у), который означает «х больше у». Заметим, что предикат может отражать как отношение, так и функцию). В первом случае выражение «х больше 5» представляется следующим образом БОЛЬШЕ(х, 5). Аналогично можно представить отношение «x любит у» предикатом вида ЛЮБИТ(х, у). Тогда выражение «Петр любит Лену» может быть представлено предикатом ЛЮБИТ(Петр, Лена). В логике первого порядка возможно использование функциональных символов. Например, мы можем использовать запись плюс(х, у), чтобы обозначить «х+у», и отец(х), что означает «Отец человека х». Предложение «х+1 больше y» и «Отец Пети любит Петю» можно символически представить в виде БОЛЬШЕ(плюс(х, 1), y) и ЛЮБИТ(отец (Петя), Петя). В приведенных примерах все выражения БОЛЬШЕ(х, 5), ЛЮБИТ(Петя, Лена), БОЛЬШЕ(плюс(х, 1), y) и ЛЮБИТ(отец(Петя), Петя) являются атомами логики первого порядка, где БОЛЬШЕ и ЛЮБИТ - предикатные символы; х - переменная; 5, Петя и Лена - индивидные символы или константы; и отец и плюс - функциональные символы.

Лекция 3. Логика высказываний