Математика

Определение Матрицей размера  называется совокупность чисел, расположенных в виде таблицы  из m строк и n столбцов.
Обозначение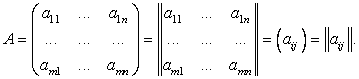
Определение Матрицы  называются  равными, , если они имеют одинаковые размеры и .
Определение Матрица называется квадратной, если .
Определение Диагональ квадратной матрицы, начинающаяся в левом верхнем, и  оканчивающаяся в правом нижнем углу, называется главной; вторая диагональ – неглавная.
Определение Квадратная матрица называется единичной, если все числа на главной диагонали равны 1, а все числа вне главной диагонали равны 0.
Определение Матрица называется нулевой (нуль-матрица), если все ее элементы равны .
Определение Суммой двух матриц  размера  называется матрица .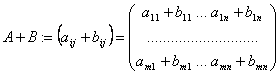
Определение Произведением матрицы  на число  называется матрица .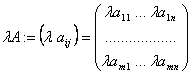
Определение Произведением матрицы  размера  на матрицу  размера  называется матрица  размера  , элементы которой вычисляются по правилу   .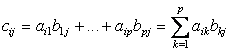
Определение  Квадратная матрица  размера  называется обратной к квадратной матрице  размера , если .
­­_____
Определение 1 Определителем (детерминантом) первого порядка квадратной матрицы  размера  называется число .
Определение 2 Определителем -го порядка квадратной матрицы  разме
ра  называется число
,
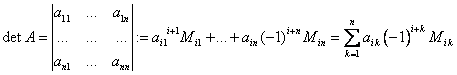где  - определитель -го порядка матрицы, которая  получается
вычеркиванием из матрицы  -той строки и -го столбца.
ЗАМЕЧАНИЕ Данная формула вычисления называется  разложением определителя  по - ой строке. Формула разложения по - ому столбцу имеет вид  
.
ТЕОРЕМА  1) Если в определителе поменялись местами две строки (два столбца), то новый определитель будет отличаться от исходного только знаком.
2) Если элементы одной строки (или столбца) умножить на одно и тоже число λ, то полученный новый определитель будет в λ  раз больше исходного.
3) Если к одной строке (столбцу) прибавить поэлементно другую строку (столбец), то полученный новый определитель совпадет с исходным.
4) Пусть два определителя одинакового порядка различаются только одной строкой (столбцом). Тогда их сумма совпадает с определителем, у которого соответствующая строка (столбец) есть сумма строк (столбцов) слагаемых определителей.
Определение  Минором порядка  матрицы   называется определитель матрицы, элементы которой стоят на пересечении каких-либо  строк и  столбцов матрицы .
Определение Рангом матрицы называется самый большой порядок у не равных нулю миноров этой матрицы.                Обозначение .
Определение Квадратная матрица  А  называется невырожденной, если , то есть когда .
Определение Матрица 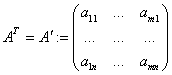 называется транспонированной к матрице .
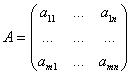Определение Число  называется алгебраическим дополнением элемента  матрицы , а матрица  - присоединенной матрицей к матрице .
ЗАМЕЧАНИЕ Если матрица  не вырождена, то существует обратная матрица , которая вычисляется по формуле .
_____

Определение Системой линейных алгебраических уравнений (СЛАУ)
называется система уравнений вида 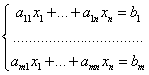 , где известные числа , называются коэффициентами СЛАУ; известные числа - свободными членами; неизвестные, искомые числа  - решением СЛАУ.
Обозначения 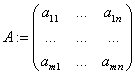 - матрица коэффициентов;  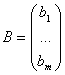- матрица свободных членов;  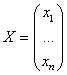- матрица неизвестных;  - расширенная матрица СЛАУ.
Эти обозначения позволяют записать СЛАУ в матричном виде .
Определение  Решить СЛАУ – это значит найти все ее решения.
Определение  СЛАУ называется совместной, если она имеет хотя бы одно решение. В противном случае СЛАУ несовместна.
Определение  Две СЛАУ одинакового порядка называются эквивалентными, если они
обе несовместны или обе совместны и имеют одинаковое множество решений.
ЗАМЕЧАНИЕ  СЛАУ  переходит в эквивалентную при следующих элементарных преобразованиях:     1) перестановка местами двух уравнений,
2) умножение какого-либо уравнения на неравное нулю число,
3) поэлементное прибавление к одному уравнению другого уравнения.
Определение  СЛАУ называется определенной, если она имеет ровно одно решение и неопределенной, если решений больше одного.
ТЕОРЕМА 1) (критерий  Кронекера-Капелли совместности СЛАУ)  СЛАУ совместна тогда и только тогда, когда ранг матрицы этой СЛАУ равен  рангу расширенной матрицы.
2) (критерий определенности СЛАУ)  Для того чтобы СЛАУ была определенной необходимо и достаточно, чтобы она была совместной и ранг матрицы коэффициентов совпадал с числом неизвестных:
3) (формулы Крамера)  Определенная СЛАУ  с помощью элементарных преобразований приводится к СЛАУ, у которой матрица коэффициентов  квадратная и . В этом случае решение СЛАУ вычисляется по формулам Крамера где -определитель, получаемый из  заменой i-ого столбца на столбец свободных членов.
СЛЕДСТВИЕ СЛАУ с  будет определенной тогда и только тогда, когда
Определение  Элементарными преобразованиями матрицы называются
следующие:   1) перестановка двух строк;
2) поэлементное умножение какой-либо строки на неравное нулю число;
3) прибавление к одной строке соответствующих элементов другой строки.
ЗАМЕЧАНИЕ СЛАУ преобразуется в эквивалентную, если ее расширенную матрицу подвергнуть элементарным преобразованиям.
Определение  Методом Гаусса называется метод решения СЛАУ с помощью элементарных преобразований по следующему правилу.
АЛГОРИТМ  Сначала обнуляются все элементы, стоящих ниже главной
диагонали последовательно по столбцам, начиная с первого; затем обнуляют
элементы над диагональю последовательно по столбцам, начиная с -го.
_____
Определение  Векторным (линейным) пространством называется множество Е, для элементов которого определены операции сложения и умножения на число, удовлетворяющие следующим аксиомам:
1)
2)
3)
4) ,
5) ,
6) ,
7) ,
8).
Определение  Линейной комбинацией (линейной алгебраической суммой) элементов  называется сумма вида , где - действительные числа, которые называются  коэффициентами разложения.
Определение Элементы  называются линейно зависимыми, если существует равная нулю линейная комбинация этих элементов, в которой не все коэффициенты равны нулю. В противном случае элементы называются  линейно независимыми.
СЛЕДСТВИЕ Элементы линейно зависимы тогда и только тогда, когда хотя бы один из них представим в виде линейной комбинации остальных.
Определение Последовательность элементов  называется  полной (базисом) в векторном пространстве  если каждый элемент из Е (единственным образом) представим в виде линейной комбинации этих элементов.
ТЕОРЕМА 2.3    1) Последовательность  является базисом в векторном пространстве тогда и только тогда, когда элементы  линейно независимы и каждый элемент из  представим в виде их линейной комбинации.
2) Базисы в векторном пространстве имеют одинаковое число элементов.
Определение  Если в векторном пространстве существует базис, то число элементов  этого базиса называется размерностью пространства Е, а пространство называется - мерным.                       Обозначение. .
Определение  Векторное пространство Е называется бесконечномерным, если в нём не существует базис с конечным числом элементов.
Определение Декартовым произведением векторных пространств  E и F называется декартово произведение соответствующих множеств ,  на котором определены операции сложения элементов и умножения их на число по правилу:
, .
ЗАМЕЧАНИЕ 1  Введенные операции на декартовом произведении удовлетворяют 8 аксиомам.
ЗАМЕЧАНИЕ 2 Аналогично определяются декартовы произведения   пространств  и .
­5 развернутых важных примеров векторных пространств.
ПРИМЕР 1  Пространство векторов с общим началом .
ПРИМЕР  2   Пространство комплексных чисел .
Определение Символ вида , обладающий свойством , называется  мнимой единицей.
Определение Выражение вида , где , называется комплексным числом (в алгебраической форме).
Обозначение  Комплексное число традиционно обозначается буквой ; множество комплексных чисел обозначается .
Определение  Вещественное число  называется действительной частью комплексного числа  , а вещественное  число  называется  коэффициентом  мнимой части  комплексного  числа.
Обозначение  .
Определение Комплексные числа ,  называются  равными, если равны их действительные и мнимые части: .
Определение Число вида  называется нулём (комплексным) и кратко обозначается . Вместо  обычно пишут  просто .
Определение Суммой комплексных чисел ,   называется комплексное число  .
Следующее определение несколько более общее, чем требуется в этом примере.
Определение Произведением комплексных чисел ,   называется комплексное число  .
ЗАМЕЧАНИЕ 1 Множество комплексных чисел  удовлетворяяет аксиомам 1)-8) векторного пространства относительно операций сложения и умножения на действительной число. Две аксиомы мы уже проверили.
ЗАМЕЧАНИЕ 2 Вещественная и мнимая единицы 1,  образуют базис в . Поэтому .
ЗАМЕЧАНИЕ 3 В определении векторного пространство элементы умножаются на действительные числа. Аналогично определяется векторное пространство, в котором элементы умножаются на комплексные числа. В этом случае говорят о векторном пространстве  над полем комплексных чисел (комплексном пространстве).
ПРИМЕР 3  Пространство  матриц размера .
Определения равенства матриц, нулевой матрицы, суммы матриц и произведения
матриц на число мы  уже давали. Из восьми аксиом проверим для множества
, например, четвертую. Матрица 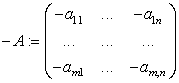 является
противоположной к матрице .
Действительно, 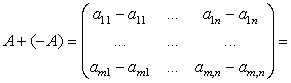 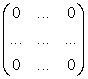- нуль-матрица.
ЗАМЕЧАНИЕ  Попарно различные матрицы размера   в количестве  
штук, у каждой из которых один элемент равен 1, а остальные равны 0, образуют
базис в пространстве .
ПРИМЕР 4  Пространство   многочленов степени .
Определение  Многочленом степени  называется функция вида , где  (или ), причем . То есть многочлен является линейной комбинацией степеней
Определение Многочлены ,  называются равными, если у них совпадают коэффициенты при одинаковых степенях
Определение  Многочлен  называется нулевым (нулем в простран стве)  и обозначается .
Определение  Суммой  многочленов  называется многочлен  .
Определение Произведением числа  на многочлен  
называется многочлен .
ЗАМЕЧАНИЕ 1 Множество  удовлетворяет аксиомам 1)-8), и потому является векторным пространством.
ЗАМЕЧАНИЕ 2 Последовательность многочленов  является базисом в . Поэтому .
 ПРИМЕР 5  Арифметическое пространство .
 мы обозначили множество  упорядоченных -ок действительных чисел.
Определение  Две -ки  называются равными, если числа, стоящие на одинаковых местах, совпадают: .
Определение  Нулём в  называется  - ка вида .
Определение Суммой двух - ок  называется  - ка  .
Определение Произведением числа  на - ку  называется  - ка
.
ЗАМЕЧАНИЕ 1  Множество  удовлетворяет аксиомам 1)-8), и потому является векторным пространством.
ЗАМЕЧАНИЕ 2  Элементы  
 образуют базис в . Следовательно, .
ЗАМЕЧАНИЕ 3 Множества чисел   не являются векторными пространствами.
_____
Определение  Отображением множества  в множество  называется правило, сопоставляющее каждому элементу из  один элемент из . В случае  отображение называется преобразованием.
Обозначение Правило обозначается латинскими буквами. Например, .
Определение  Множество  называется областью определения отображения ;
множество  - областью значений отображения; множество
- множеством значений (образом отображения) .
Определение  Отображение  из векторного пространства  в векторное  пространство  называется линейным оператором (отображением), если
.
Определение  Линейный оператор  называется изоморфизмом векторных пространств  и , если он переводит разные элементы в разные:  , и каждый элемент из  является образом некоторого элемента из : . При этом пространства называются изоморфными.
ЗАМЕЧАНИЕ 1 Это понятие позволяет формулировать результаты для векторного пространства на языке изоморфного ему пространства. Иногда это оказывается удобным.
Определение Линейный оператор из  в  называется  линейной формой (линейным функционалом).
Определение  Отображение  из векторного пространства  в вектор ное пространство  называется - линейным полилинейным) отображением, если оно является линейным отображением из  в  по каждой переменной , , при фиксированных остальных.
Определение - линейное отображение из  в  называется - линейной (полилинейной) формой.
ЗАМЕЧАНИЕ  2 - линейное отображение  принято называть билинейным отображением .
Определение Билинейная форма  называется скалярным произведением на векторном пространстве , если она  обладает свойствами:
1) ;  2) ;  3)  
Обозначение  .
Определение Отображение , называется нормой, если оно обладает
свойствами:
1);      2) ;     3) .
ЗАМЕЧАНИЕ 1  Понятие нормы, как нетрудно заметить по свойствам, обобщает понятие длины вектора в .
ЗАМЕЧАНИЕ 2   Каждое скалярное произведение  порождает норму в  по правилу .
СЛЕДСТВИЕ  Естественное скалярное произведение в  обладает свойством  .
Определение -мерным евклидовым (точечным) пространством называется тройка объектов: -мерное векторное пространство , какое-либо скалярное произведение  на нём и множество “точек” , которые согласованы следующим образом:
1)  каждой упорядоченной паре точек  поставлен в соответствие один элемент
, который обозначают ;          2)  существует единственная точка  со свойством ;  3)    .
Обозначение .
Определение  Расстоянием между двумя точками   называется число
.
Определение мерным аффинным пространством называется пара  со свойствами 1) -3).
Определение мерным евклидовым векторным пространством называется пара .
Определение  - мерным арифметическим евклидовым пространством   называет ся тройка объектов: арифметическое пространство , естественное скалярное  произведение  и множество ”точек” . При этом точки ,  свяжем с вектором из  по правилу . Тогда расстояние между точками ,    вычисляется по формуле
.