Интегральное исчисление функций одной переменной
Определение Пусть функция ![]() определена на интервале
определена на интервале ![]() . Дифференцируемая на
. Дифференцируемая на ![]() функция
функция ![]() называется первообразной функции
называется первообразной функции ![]() , если
, если ![]() .
.
ЗАМЕЧАНИЕ Если ![]() есть первообразная функции
есть первообразная функции ![]() на
на ![]() , то любая другая первообразная имеет вид
, то любая другая первообразная имеет вид ![]() , где
, где ![]() - произвольная постоянная.
- произвольная постоянная.
Определение Множество всех первообразных функции называется неопределенным интегралом этой функции.
СЛЕДСТВИЕ Два интеграла совпадают тогда и только тогда, когда они имеют общую функцию.
Определение Проинтегрировать функцию – это значит ее первообразную.
Обозначение ![]() .
.
Имеет место такая таблица первообразных от элементарных функций.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ТЕОРЕМА (правила и формулы интегрирования)
1) ![]() , если хотя бы два
, если хотя бы два
из трех интегралов существуют. 2) (формула замены переменных) Если
![]() и функция
и функция ![]() непрерывно дифференцируема на
непрерывно дифференцируема на ![]() , то на
, то на ![]() существует интеграл функции
существует интеграл функции ![]() и он вычисляется по формуле
и он вычисляется по формуле ![]() . 3) (формула интегрирования по частям) Если функции
. 3) (формула интегрирования по частям) Если функции ![]() дифференцируемы на
дифференцируемы на ![]() , и существует один из интегралов
, и существует один из интегралов ![]() , то существует второй интеграл и имеет место равенство
, то существует второй интеграл и имеет место равенство![]() .
.
______
Определение Пусть функция ![]() имеет производную порядка
имеет производную порядка ![]() в точке
в точке ![]() .
. ![]()
называется нулем кратности ![]() функции
функции ![]() (корнем кратности
(корнем кратности ![]() уравнения
уравнения ![]() ), если
), если ![]() .
.
В разделе теории функций комплексного переменного будет доказана
ТЕОРЕМА (Гаусс) Многочлен ![]() -ой степени
-ой степени ![]() , имеет
, имеет
ровно ![]() корней, если учитывать кратность каждого корня и все комплексные корни. Если
корней, если учитывать кратность каждого корня и все комплексные корни. Если ![]() его корни, то имеет место представление
его корни, то имеет место представление
![]() .
.
СЛЕДСТВИЕ Многочлен с действительными коэффициентами единственным образом представим в виде произведения степеней одно членов ![]() и квадратных трехчленов с действительными коэффициентами
и квадратных трехчленов с действительными коэффициентами ![]() , имеющих сопряженные комплексные нули.
, имеющих сопряженные комплексные нули.
Определение Рациональная функция ![]() называется правильной дробью, если
называется правильной дробью, если ![]() .
.
ЗАМЕЧАНИЕ Неправильную рациональную функцию с помощью деления числителя на знаменатель можно представить в виде суммы многочлена и правильной рациональной функции.
Определение Рациональные функции с вещественными коэффициентами вида ![]() или вида
или вида ![]() , где квадратный трехчлен имеет комплексные сопряженные нули, называются простейшими дробями.
, где квадратный трехчлен имеет комплексные сопряженные нули, называются простейшими дробями.
ЗАМЕЧАНИЕ Каждая правильная дробь единственным образом представима в виде суммы простейших дробей. Алгоритм представления называется методом неопределенных коэффициентов.
ЗАМЕЧАНИЕ 1 Пусть ![]() - рациональная функция двух переменных, а
- рациональная функция двух переменных, а ![]() - дробно-линейная функция. Тогда интеграл вида
- дробно-линейная функция. Тогда интеграл вида 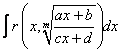 сводится к интегралу от рациональной функции с помощью замены переменной
сводится к интегралу от рациональной функции с помощью замены переменной ![]() .
.
ЗАМЕЧАНИЕ 2 Интеграл вида ![]() приводится к интегралу о рациональной функции с помощью универсальной подстановки
приводится к интегралу о рациональной функции с помощью универсальной подстановки ![]() . ЗАМЕЧАНИЕ 3 Следующие интегралы специального вида приводятся к
. ЗАМЕЧАНИЕ 3 Следующие интегралы специального вида приводятся к
интегралам от рациональных функций с помощью соответствующих замен
![]()
![]() .
.
ЗАМЕЧАНИЕ 4 К интегралам от рациональных функций с помощью двух последова тельных замен приводятся и такие интегралы ![]()
![]()
![]() .
.
____
Определение Разобьем отрезок ![]() точками
точками ![]() на
на ![]() попарнонепе ресе кающихся отрезков, и обозначим это разбиение
попарнонепе ресе кающихся отрезков, и обозначим это разбиение ![]() . Длина наибольшего из отрез ков
. Длина наибольшего из отрез ков ![]() , где
, где ![]() , называется диаметром разбиения
, называется диаметром разбиения ![]() отрезка
отрезка ![]() .
.
ЗАМЕЧАНИЕ При ![]() число
число ![]() отрезков разбиения стремится к бесконечно сти, а длины всех этих отрезков равномерно стремятся к нулю.
отрезков разбиения стремится к бесконечно сти, а длины всех этих отрезков равномерно стремятся к нулю.
Определение Пусть на отрезке ![]() задана функция. Произведем разбиение
задана функция. Произведем разбиение ![]() , и выберем на
, и выберем на ![]() -ом отрезке разбиения точку
-ом отрезке разбиения точку ![]() . Обозначим
. Обозначим ![]() . Сумма вида
. Сумма вида ![]() называется интегральной суммой. Если существует конечный предел
называется интегральной суммой. Если существует конечный предел ![]() , равномерный относительно выбора точек
, равномерный относительно выбора точек ![]() :
:
![]() ,
,
то он называется определенным интегралом (Римана) функции ![]() на отрезке
на отрезке ![]() , а
, а ![]() - интегрируемой по Риману функцией. Обозначение
- интегрируемой по Риману функцией. Обозначение 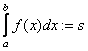 .
.
Определение Пусть на отрезке ![]() заданы две функции
заданы две функции ![]() . Множество точек
. Множество точек ![]() называется криволинейной трапецией
называется криволинейной трапецией ![]() .
.
Определение Если существует определенный интеграл
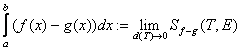 ,
,
то он называется площадью криволинейной трапеции.
_____
Определение Функция ![]() называется кусочно непрерывной на
называется кусочно непрерывной на ![]() , если она непрерывна на
, если она непрерывна на ![]() за исключением конечного числа точек разрыва первого рода.
за исключением конечного числа точек разрыва первого рода.
ЗАМЕЧАНИЕ Кусочно непрерывная функция ограничена на ![]() .
.
Определение Функция ![]() называется кусочно монотонной на
называется кусочно монотонной на ![]() , если она ограничена и для некоторого разбиения
, если она ограничена и для некоторого разбиения ![]()
![]() не убывает или не возрастает на каждом интервале
не убывает или не возрастает на каждом интервале ![]() .
.
ТЕОРЕМА (существования интеграла Римана) 1) Если ![]() кусочно непрерывна
кусочно непрерывна
или кусочно монотонна на ![]() , то интеграл
, то интеграл 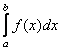 существует. 2) Еслиинтеграл
существует. 2) Еслиинтеграл
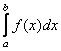 существует, то
существует, то ![]() ограничена на
ограничена на ![]() .
.
ТЕОРЕМА (свойства определенного интеграла)
1) 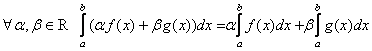 , если хотя бы два из этих интегралов существуют
, если хотя бы два из этих интегралов существуют ![]() .
.
2) Если ![]() , то
, то 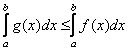 . 3) Если
. 3) Если ![]() интегрируема на
интегрируема на ![]() и
и ![]() , то
, то  .
.
4) (теорема о среднем) Если ![]() непрерывна, а
непрерывна, а ![]() знакопостоянна на
знакопостоянна на ![]() , то
, то 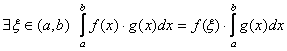 при условии существования интегралов.
при условии существования интегралов.
5) 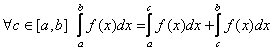 .
.
ЗАМЕЧАНИЕ Если при определении определенного интеграла разбиение отрезка ![]() проводить убывающей последовательностью точек
проводить убывающей последовательностью точек ![]() , то
, то 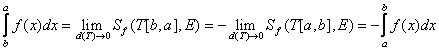 .
.
Это согласуется с равенством 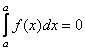 .
.
_____
Кроме знания факта существования интеграла и его свойств необходим еще алгоритм вычисления определенного интеграла.
Определение Пусть ![]() интегрируема на отрезке
интегрируема на отрезке ![]() . Можно оказать, что она
. Можно оказать, что она
интегрируема на каждом ![]() . Функция
. Функция 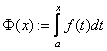 называется
называется
интегралом с переменным верхним пределом.
ТЕОРЕМА 1) Если ![]() непрерывна на
непрерывна на ![]() , то функция
, то функция 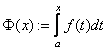 является ее первообразной.
является ее первообразной.
2) (формула Ньютона-Лейбница) Если ![]() непрерывна на
непрерывна на ![]() и
и ![]() какая-либо ее первообразная, то
какая-либо ее первообразная, то 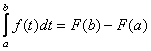 .
.
3) (формула замены переменной) Если ![]() непрерывна на
непрерывна на ![]() , а функция
, а функция ![]() непрерывно дифференцируема на
непрерывно дифференцируема на ![]() и
и ![]() , то
, то 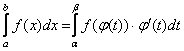 .
.
4) (формула интегрирования по частям) Если функции ![]() непрерывно
непрерывно
дифференцируемы на ![]() , то
, то 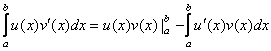 , где
, где
![]() .
.
ЗАМЕЧАНИЕ Если функция ![]() интегрируемая и четная (нечетная) на отрезке
интегрируемая и четная (нечетная) на отрезке ![]() , то
, то 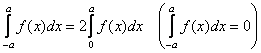 .
.
____
ЗАМЕЧАНИЕ Если ![]() непрерывно дифференцируема на
непрерывно дифференцируема на ![]() , то для любого разбиения
, то для любого разбиения ![]() этого отрезка по формуле Лагранжа найдется последовательность точек
этого отрезка по формуле Лагранжа найдется последовательность точек ![]() со свойством
со свойством 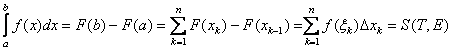 , то есть определенный интеграл совпадает с некоторой интегральной суммой функции.
, то есть определенный интеграл совпадает с некоторой интегральной суммой функции.
Определение Пусть ![]() определена на
определена на ![]() . Сумма вида
. Сумма вида ![]() , где
, где ![]() , называется квадратурной формулой, числа
, называется квадратурной формулой, числа ![]() - узлами квадратурной формулы, а числа
- узлами квадратурной формулы, а числа ![]() - коэффициентами. Число
- коэффициентами. Число 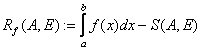 называется остаточным членом квадратурной формулы.
называется остаточным членом квадратурной формулы.
Из многочисленных приближенных формул вычисления интеграла приведем формулу прямоугольников.
ЗАМЕЧАНИЕ Разобьем ![]() равноотстоящими точками
равноотстоящими точками![]() ,
,
на ![]() отрезков одинаковой длины. Если функция
отрезков одинаковой длины. Если функция ![]() имеет непрерывную производную второго порядка на
имеет непрерывную производную второго порядка на ![]() , то квадратурная формула прямоугольников имеет вид
, то квадратурная формула прямоугольников имеет вид 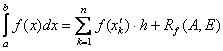 , где
, где ![]() и
и
![]() .
.
_____
Определение Пусть кривая ![]() задана параметрическим уравнением
задана параметрическим уравнением ![]() . Фиксируем разбиение
. Фиксируем разбиение ![]() и выберем точки кривой
и выберем точки кривой ![]() . Так как длина отрезка
. Так как длина отрезка ![]() ,
, ![]() равна
равна ![]() , то длина ломаной
, то длина ломаной ![]() , составленной из этих отрезков и вписанной в
, составленной из этих отрезков и вписанной в ![]() , равна
, равна ![]() . Если существует конечный
. Если существует конечный ![]() , то он называется длиной кривой
, то он называется длиной кривой ![]() , а сама кривая называется спрямляемой.
, а сама кривая называется спрямляемой.
Определение Кривая ![]() называется кусочно гладкой, если ее можно разбить на конечное число гладких кусков.
называется кусочно гладкой, если ее можно разбить на конечное число гладких кусков.
ТЕОРЕМА 1) (вычисление длины дуги) Если кривая ![]() кусочно гладкая, то она спрямляемая. Ее длина вычисляется по формуле
кусочно гладкая, то она спрямляемая. Ее длина вычисляется по формуле 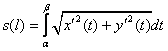 . В случае задания
. В случае задания ![]() функцией
функцией ![]() ,
,  . В случае задания
. В случае задания ![]() в полярной системе координат:
в полярной системе координат: ![]() ,
, ![]() ,
, 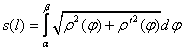 .
.
2) (вычисление площади) Пусть дан криволинейный сектор ![]() , где функция
, где функция ![]() , непрерывна. Тогда площадь сектора существует и вычисляется по формуле
, непрерывна. Тогда площадь сектора существует и вычисляется по формуле 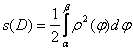 .
.
3) (вычисление объема) Пусть функция ![]() непрерывна и неотрицательна. Тогда объем тела, получаемого вращением криволинейной трапеции
непрерывна и неотрицательна. Тогда объем тела, получаемого вращением криволинейной трапеции ![]() вокруг отрезка
вокруг отрезка ![]() оси
оси ![]() , существует и вычисляется по формуле
, существует и вычисляется по формуле 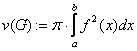 .
.
4) (вычисление площади поверхности) Пусть функция ![]() кусочно гладкая и неотрицательна. Тогда площадь боковой поверхности
кусочно гладкая и неотрицательна. Тогда площадь боковой поверхности ![]() тела, получае мого вращением криволинейной трапеции
тела, получае мого вращением криволинейной трапеции ![]() вокруг отрезка
вокруг отрезка ![]() оси
оси ![]() , существует и вычисляется по формуле
, существует и вычисляется по формуле
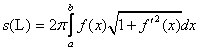 .
.
____
Определение Пусть функция ![]() определена на
определена на ![]() и интегрируема на каждом
и интегрируема на каждом
отрезке ![]() . Если существует конечный предел
. Если существует конечный предел  , то он
, то он
называется несобственным интегралом функции ![]() на промежутке
на промежутке ![]() . В
. В
этом случае говорят, что несобственный интеграл сходится.
ЗАМЕЧАНИЕ 1 Аналогично определяется несобственный интеграл  . Несобственный интеграл
. Несобственный интеграл 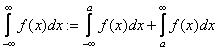 , при условии, что несобственные интегралы в правой части существуют при некотором
, при условии, что несобственные интегралы в правой части существуют при некотором ![]() .
.
ЗАМЕЧАНИЕ 2 (интегральный признак Коши) Пусть для знакоположительного ряда ![]() и положительной невозрастающей непрерывной на
и положительной невозрастающей непрерывной на ![]() функции
функции ![]() имеют место равенства
имеют место равенства ![]() . Тогда несобственный интеграл
. Тогда несобственный интеграл 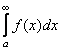 и ряд
и ряд ![]() одновременно сходятся или расходятся.
одновременно сходятся или расходятся.
ЗАМЕЧАНИЕ 3 (признаки сходимости несобственного интеграла)
1) Пусть ![]() ,
, ![]() интегрируема на каждом отрезке
интегрируема на каждом отрезке ![]() и сходится интеграл
и сходится интеграл 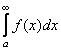 . Тогда сходится интеграл
. Тогда сходится интеграл 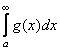 .
.
2) Пусть ![]() ,
, ![]() интегрируемы на каждом отрезке
интегрируемы на каждом отрезке ![]() и
и
интеграл 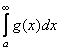 расходится. Тогда расходится интеграл
расходится. Тогда расходится интеграл 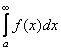 .
.
3) Пусть ![]() ,
, ![]() интегрируемы на каждом отрезке
интегрируемы на каждом отрезке ![]() и существует конечный положительный предел
и существует конечный положительный предел ![]() . Тогда интегралы
. Тогда интегралы 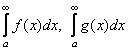 одновременно сходятся или расходятся.
одновременно сходятся или расходятся.
_____
Определение Пусть функция ![]() определена на полуинтервале
определена на полуинтервале ![]() , не ограничена в окрестности точки
, не ограничена в окрестности точки ![]() и интегрируема на каждом
и интегрируема на каждом ![]() . Если существует конечный предел
. Если существует конечный предел 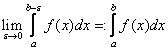 , то он называется несобственным интегралом от неограниченной функции
, то он называется несобственным интегралом от неограниченной функции ![]() на отрезке
на отрезке ![]() . В этом случае говорят, что несобственный интеграл сходится.
. В этом случае говорят, что несобственный интеграл сходится.
ЗАМЕЧАНИЕ 1 Аналогично определяется несобственный интеграл 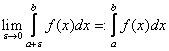 . Пусть
. Пусть ![]() определена на отрезке
определена на отрезке ![]() за исключением точки
за исключением точки ![]() , в окрестности которой она не ограничена. Несобственный интеграл
, в окрестности которой она не ограничена. Несобственный интеграл  при условии, что несобственные интегралы в правой части существуют.
при условии, что несобственные интегралы в правой части существуют.
ЗАМЕЧАНИЕ 2 Аналогичные признаки сходимости имеют место для несобственного интеграла на конечном отрезке.