Линейная алгебра и аналитическая геометрия
_____
Определение В ![]() мерном евклидовом пространстве
мерном евклидовом пространстве ![]() совокупность каких-либо точки
совокупность каких-либо точки ![]() и базиса
и базиса ![]() называется декартовой системой координат (ДСК).
называется декартовой системой координат (ДСК).
Определение Символом Кронекера называется отображение ![]() , определяемое по правилу
, определяемое по правилу ![]() , если
, если ![]() и
и ![]() , если
, если ![]() .
.
Определение Базис называется ортонормированным, если ![]() .
.
ЗАМЕЧАНИЕ Элементы ![]() такого базиса попарно перпендикулярны:
такого базиса попарно перпендикулярны:
![]() и их нормы равны единице:
и их нормы равны единице: ![]()
![]() . Здесь аналогия со школой, когда равенство нулю скалярного произведения означало ортогональность векторов, а квадрат модуля вектора совпадал со скалярным произведением вектора на себя.
. Здесь аналогия со школой, когда равенство нулю скалярного произведения означало ортогональность векторов, а квадрат модуля вектора совпадал со скалярным произведением вектора на себя.
Определение ДСК, в которой выделенный базис является ортонормированным, называется прямоугольной декартовой системой координат (ПДСК).
ЗАМЕЧАНИЕ Всюду ниже ДСК предполагается прямоугольной, если не оговорено противное.
Определение Коэффициенты разложения элемента ![]() по базису
по базису ![]() , называются, как и ранее, координатами (компонентами) вектора
, называются, как и ранее, координатами (компонентами) вектора ![]() в базисе
в базисе ![]() .
.
Обозначение ![]() . Это обозначение объясняется изоморфизмом между пространствами
. Это обозначение объясняется изоморфизмом между пространствами ![]() и
и ![]() , устанавливаемым линейным оператором
, устанавливаемым линейным оператором ![]() , где
, где ![]() .
.
Определение Радиусом-вектором точки ![]() и ПДСК называется вектор
и ПДСК называется вектор ![]() .
.
Определение Координатами точки ![]() в ПДСК называются компоненты её радиуса-вектора
в ПДСК называются компоненты её радиуса-вектора ![]() .
.
Обозначение Если ![]() , то
, то ![]() .
.
Определение Пусть дана матрица ![]() размера
размера ![]()
![]() и последовательность чисел
и последовательность чисел ![]() .
. ![]() -мерной плоскостью в
-мерной плоскостью в ![]() -мерном евклидовом пространстве
-мерном евклидовом пространстве ![]() с фиксированной ПДСК называется множество точек
с фиксированной ПДСК называется множество точек ![]() , координаты которых удовлетворяют СЛАУ
, координаты которых удовлетворяют СЛАУ 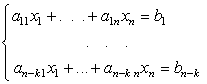 .
.
Определение Прямой в ![]() называется
называется ![]() -плоскость.
-плоскость.
Определение Полярной системой координат в ![]() называется совокупность точки
называется совокупность точки ![]() (-полюс) и луча с началом в этой точке (-полярная ось).
(-полюс) и луча с началом в этой точке (-полярная ось).
Определение Полярными координатами точки ![]() называется пара чисел
называется пара чисел ![]() , где
, где ![]() угол между полярной осью и вектором
угол между полярной осью и вектором ![]() , отсчитываемый против часовой стрелки.
, отсчитываемый против часовой стрелки.
ЗАМЕЧАНИЕ 1 Каждая точка евклидовой плоскости ![]() вполне определяется заданием полярных координат.
вполне определяется заданием полярных координат.
ЗАМЕЧАНИЕ 2 Совместим прямоугольную декартову и полярную системы координат так, чтобы начало координат совпадало с полюсом, а ось ![]() - с полярной осью Тогда декартовы координаты
- с полярной осью Тогда декартовы координаты ![]() точки
точки ![]() и ее полярные координаты связаны, как легко усмотреть из рисунка, равенствами
и ее полярные координаты связаны, как легко усмотреть из рисунка, равенствами
![]() ,
, 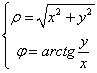 .
.
Определение В ![]() с ПДСК фиксируем точку
с ПДСК фиксируем точку ![]() . Тройка чисел
. Тройка чисел ![]() , где
, где ![]() , называется сферическими координатами точки
, называется сферическими координатами точки ![]() .
.
ЗАМЕЧАНИЕ 1 Каждая точка ![]() вполне определяется своими сферическими координатами.
вполне определяется своими сферическими координатами.
ЗАМЕЧАНИЕ 2 Так как ![]() , то декартовы и сферические координаты точки
, то декартовы и сферические координаты точки ![]() связаны равенствами
связаны равенствами 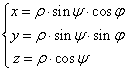 .
.
Определение В ![]() с ПДСК фиксируем точку
с ПДСК фиксируем точку ![]() . Тройка чисел
. Тройка чисел ![]() , где
, где ![]() называется цилиндрическими координатами точки
называется цилиндрическими координатами точки ![]() .
.
ЗАМЕЧАНИЕ 1 Каждая точка ![]() вполне определяется своими цилиндрическими координатами.
вполне определяется своими цилиндрическими координатами.
ЗАМЕЧАНИЕ 2 В ПДСК декартовы и цилиндрические координаты точки ![]() связаны равенствами:
связаны равенствами: 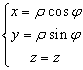 .
.
_____
Определение Пусть даны ось ![]() (
(![]() направленная прямая) и вектор
направленная прямая) и вектор ![]() . Опустим перпендикуляры из его концов на ось. Проекцией вектора
. Опустим перпендикуляры из его концов на ось. Проекцией вектора ![]() на ось
на ось ![]() называется расстояние между основаниями этих перпендикуляров, взятое со знаком "+", если
называется расстояние между основаниями этих перпендикуляров, взятое со знаком "+", если ![]() , со знаком "-", если
, со знаком "-", если ![]() и равное нулю, если
и равное нулю, если ![]() . Правило, сопоставляющее каждому вектору его проекцию на ось, называется операцией проектирования. Обозначение пр
. Правило, сопоставляющее каждому вектору его проекцию на ось, называется операцией проектирования. Обозначение пр![]() .
.
ТЕОРЕМА 1) пр![]() . 2)
. 2) ![]() пр
пр![]() пр
пр![]() + пр
+ пр![]() .
.
3) ![]() пр
пр![]()
![]()
![]() пр
пр![]() , то есть операция проектирования является линейным функционалом. 4) Фиксируем ПДСК в
, то есть операция проектирования является линейным функционалом. 4) Фиксируем ПДСК в ![]() . Тогда проекции вектора на оси
. Тогда проекции вектора на оси
координат ![]() совпадают с компонентами этого вектора в базисе
совпадают с компонентами этого вектора в базисе ![]() : если
: если ![]() , то
, то ![]() пр
пр![]() ,
, ![]() пр
пр![]() ,
, ![]() пр
пр![]() ;
;
5) Косинусы ![]() ,
, ![]() ,
, ![]() называются направляющими
называются направляющими
косинусами вектора ![]() и связаны равенством
и связаны равенством ![]()
![]()
![]() =1.
=1.
СЛЕДСТВИЕ Скалярное произведение векторов связано с операцией проектирования равенством ![]() .
.
ЗАМЕЧАНИЕ Пусть точка ![]() делит отрезок
делит отрезок ![]() с концами в точках
с концами в точках
![]() в отношении
в отношении ![]() . Тогда координаты
. Тогда координаты ![]() вычисляются по
вычисляются по
формулам ![]() .
.
____
В следующей теореме собраны свойства скалярного произведения.
ТЕОРЕМА 1) ![]() . 2)
. 2) ![]() . 3)
. 3) ![]() .
.
4) Скалярное произведение является билинейной формой на ![]() .
.
5) Если в ПДСК ![]() , то
, то ![]() .
.
Определение (физический смысл скалярного произведения) Работой постоянной силы ![]() по перемещению материальной точки из начала в конец вектора
по перемещению материальной точки из начала в конец вектора ![]() называется величина
называется величина ![]() .
.
_____
Определение Упорядоченная тройка некомпланарных векторов ![]() с общим началом называется правой (левой), если из конца вектора
с общим началом называется правой (левой), если из конца вектора ![]() движение от
движение от ![]() к
к ![]() по кратчайшему из двух углов происходит против (по) часовой стрелки(е).
по кратчайшему из двух углов происходит против (по) часовой стрелки(е).
Определение Векторным произведением векторов ![]() называется вектор
называется вектор ![]() , если
, если ![]() . В противном случае векторным произведением
. В противном случае векторным произведением ![]() называется вектор
называется вектор ![]() , который вполне определяется свойствами:
, который вполне определяется свойствами:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() - правая тройка векторов.
- правая тройка векторов.
Определение Смешанным произведением трех векторов ![]() называется число
называется число ![]() .
.
ЗАМЕЧАНИЕ 1 (геометрический смысл модуля)
1) ![]() численно равен площади параллелограмма, построенного на векторах
численно равен площади параллелограмма, построенного на векторах ![]() как на сторонах. 2)
как на сторонах. 2) ![]() численно равен объему призмы, построенной на векторах
численно равен объему призмы, построенной на векторах ![]() как на ребрах
как на ребрах ![]() .
.
ЗАМЕЧАНИЕ 2 ![]() .
.
В следующей теореме собраны свойства векторного произведения.
ТЕОРЕМА 1) Векторное произведение является билинейным отображением из
![]() в
в ![]() . 2) Если
. 2) Если ![]() , то
, то 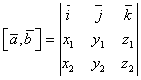 .
.
СЛЕДСТВИЕ Ненулевые векторы ![]() параллельны тогда и только тогда, когда
параллельны тогда и только тогда, когда ![]() .
.
Векторное произведение имеет до десятка физических смыслов. Приведем наиболее характерные.
Определение (физический смысл векторного произведения). Моментом относительно точки ![]() силы
силы ![]() , приложенной к точке
, приложенной к точке ![]() , называется вектор
, называется вектор ![]() .
.
Определение (физический смысл векторного произведения) Пусть материальная точка ![]() вращается по окружности (с центром
вращается по окружности (с центром ![]() ) с линейной скоростью
) с линейной скоростью ![]() . Вектором угловой скорости вращения этой точки относительно цента
. Вектором угловой скорости вращения этой точки относительно цента ![]() называется расположенный на оси вращения вектор
называется расположенный на оси вращения вектор ![]() , определяемый равенством
, определяемый равенством ![]() . Это равенство называется формулой Эйлера.
. Это равенство называется формулой Эйлера.
В следующей теореме собраны свойства смешанного произведения.
ТЕОРЕМА 1) ![]() (векторы
(векторы ![]() компланарны)
компланарны)
2) Смешанное произведение является 3– линейной формой: ![]() .
.
3) Если ![]() , то
, то 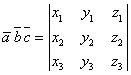 .
.
Напомним, что плоскостью L (2 - плоскостью) в ![]() с фиксированной ПДСК называется множество точек, координаты которых удовлетворяют уравнению
с фиксированной ПДСК называется множество точек, координаты которых удовлетворяют уравнению ![]() , где
, где ![]() . Определение Вектором нормали к плоскости называется вектор, перпендикуляр ный любому вектору, начало и конец которого лежат в этой плоскости . Определение Углом между плоскостями называется угол между их векторами нормалей. В зависимости от выбранных векторов нормалей этот угол имеет два значения. ТЕОРЕМА Пусть заданы 3 плоскости
. Определение Вектором нормали к плоскости называется вектор, перпендикуляр ный любому вектору, начало и конец которого лежат в этой плоскости . Определение Углом между плоскостями называется угол между их векторами нормалей. В зависимости от выбранных векторов нормалей этот угол имеет два значения. ТЕОРЕМА Пусть заданы 3 плоскости ![]() ;
; 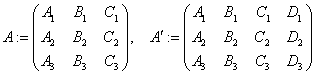 . Тогда имеют место следующие утверждения. 1)
. Тогда имеют место следующие утверждения. 1) 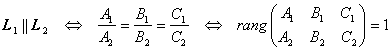 . 2)
. 2)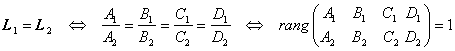 . 3) Плоскости
. 3) Плоскости ![]() пересекаются в одной точке тогда и только тогда, когда
пересекаются в одной точке тогда и только тогда, когда ![]() .
.
4) плоскости ![]() пересекаются по одной прямой тогда и только тогда, когда
пересекаются по одной прямой тогда и только тогда, когда ![]() . 5)
. 5) 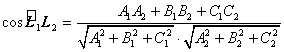 . 6) Расстояние от точки
. 6) Расстояние от точки ![]() до плоскости
до плоскости ![]() вычисляется по формуле
вычисляется по формуле
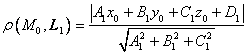 .
.
Определение Пусть векторы ![]() не коллинеарны, и задана точка
не коллинеарны, и задана точка ![]() . Формула
. Формула 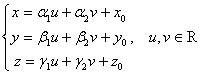 , определяющая множество точек с координатами
, определяющая множество точек с координатами ![]() в
в ![]() , называется параметрическим уравнением плоскости. ЗАМЕЧАНИЕ а) Если плоскость задана параметрическим уравнением, то ее общее уравнение имеет вид
, называется параметрическим уравнением плоскости. ЗАМЕЧАНИЕ а) Если плоскость задана параметрическим уравнением, то ее общее уравнение имеет вид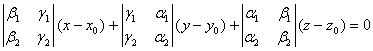 . б) Если плоскость задана уравнением
. б) Если плоскость задана уравнением ![]() и для определенности
и для определенности ![]() , то ее параметрическое уравнение можно задать, например, в виде
, то ее параметрическое уравнение можно задать, например, в виде 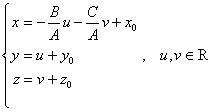 . Следующее замечание доказывается аналогично теореме.
. Следующее замечание доказывается аналогично теореме.
ЗАМЕЧАНИЕ Пусть в какой-либо ПДСК в евклидовой плоскости ![]() заданы две прямые
заданы две прямые ![]() уравнениями
уравнениями ![]() . Тогда справедливы следующие утверждения. 1)
. Тогда справедливы следующие утверждения. 1) ![]() . 2)
. 2) ![]() . 3)_
. 3)_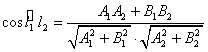 . 4) Расстояние от точки
. 4) Расстояние от точки ![]() до прямой
до прямой ![]() вычисляется по формуле
вычисляется по формуле 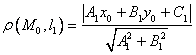 .
.
_____
Определение Множество точек, координаты которых ![]() удовлетворяют СЛАУ
удовлетворяют СЛАУ 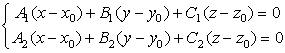 , (1) где
, (1) где 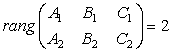 , называется уравнением прямой в
, называется уравнением прямой в ![]() , проходящей через точку
, проходящей через точку ![]() . Определение Пусть даны вектор
. Определение Пусть даны вектор ![]() и точка
и точка ![]() . Система уравнений вида
. Система уравнений вида ![]() (2)
(2)
называется каноническим уравнением прямой.
Формула, 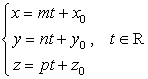 , (3) определяющая множество точек в
, (3) определяющая множество точек в ![]() с координатами
с координатами ![]() , называется параметрическим уравнением прямой. ЗАМЕЧАНИЕ 1 Направляющий вектор
, называется параметрическим уравнением прямой. ЗАМЕЧАНИЕ 1 Направляющий вектор ![]() параллелен любому вектору, начало и конец которого лежат на этой прямой. ЗАМЕЧАНИЕ 2 Уравнения (1), (2), (3), в которых
параллелен любому вектору, начало и конец которого лежат на этой прямой. ЗАМЕЧАНИЕ 2 Уравнения (1), (2), (3), в которых 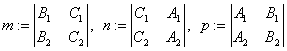 задают одну и ту же прямую в
задают одну и ту же прямую в ![]() . Определение Углом между двумя прямыми называется угол между направляю щими векторами этих прямых. Этот угол принимает два значения. ТЕОРЕМА Пусть даны две прямые
. Определение Углом между двумя прямыми называется угол между направляю щими векторами этих прямых. Этот угол принимает два значения. ТЕОРЕМА Пусть даны две прямые ![]() и плоскость
и плоскость ![]() . Тогда имеют место утверждения. 1)
. Тогда имеют место утверждения. 1) ![]() скрещиваются
скрещиваются 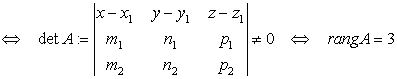 . 2)
. 2) 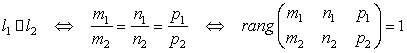 3)
3) 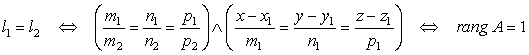 . 4)
. 4) ![]() пересекаются
пересекаются 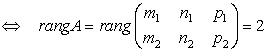 . 5)
. 5) 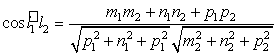 . 6) Расстояние от точки
. 6) Расстояние от точки ![]() до прямой
до прямой ![]() вычисляется по формуле
вычисляется по формуле
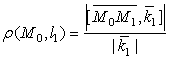 . 7) Расстояние между двумя прямыми вычисляется по формуле
. 7) Расстояние между двумя прямыми вычисляется по формуле 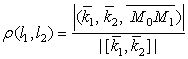 .
.
Приведем без доказательства виды уравнения прямой в евклидовой плоскости ![]() . ЗАМЕЧАНИЕ а)
. ЗАМЕЧАНИЕ а) ![]() - каноническое уравнение прямой на плоскости. б)
- каноническое уравнение прямой на плоскости. б) ![]() - уравнение прямой, проходящей через две точки
- уравнение прямой, проходящей через две точки ![]() . в)
. в) 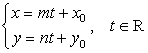 - параметрическое уравнение прямой. г)
- параметрическое уравнение прямой. г) ![]() - уравнение прямой "в отрезках на осях
- уравнение прямой "в отрезках на осях ![]() ". Название объясняя ется тем, что прямая пересекается с осью
". Название объясняя ется тем, что прямая пересекается с осью ![]() в точке
в точке ![]() , а с осью
, а с осью ![]() - в точке
- в точке ![]() . д)
. д) ![]() - нормальное уравнение прямой, где
- нормальное уравнение прямой, где ![]() - единичный вектор нормали к прямой, а
- единичный вектор нормали к прямой, а ![]() есть проекция радиусоввекторов точек
есть проекция радиусоввекторов точек ![]() прямой на направление вектора нормали.
прямой на направление вектора нормали.
_____
Определение Кривой второго порядка в 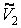 называется множество точек, координаты которых в какой-либо ПДСК удовлетворяют уравнению
называется множество точек, координаты которых в какой-либо ПДСК удовлетворяют уравнению 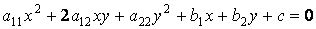 , где
, где 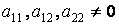 одновременно.
одновременно.
ЗАМЕЧАНИЕ Уравнение окружности можно задать и в параметрическом виде
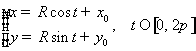 , в чем нетрудно убедиться подстановкой в предыдущее уравнение.
, в чем нетрудно убедиться подстановкой в предыдущее уравнение.
Опредление Эллипс – множество точек в  , сумма расстояний от каждой и которых до двух заданных точек (фокусов) есть величина постоянная.
, сумма расстояний от каждой и которых до двух заданных точек (фокусов) есть величина постоянная.
ЗАМЕЧАНИЕ 1 Фиксируем ПДСК в ![]() . Обозначим сумму расстояний до фокусов
. Обозначим сумму расстояний до фокусов ![]() , и расположим фокусы на оси
, и расположим фокусы на оси ![]() симметрично относительно начала координат:
симметрично относительно начала координат: ![]() .
.
Положим ![]() . Тогда уравнение эллипса (каноническое) будет иметь вид
. Тогда уравнение эллипса (каноническое) будет иметь вид
![]() .
.
ЗАМЕЧАНИЕ 2 В каноническом уравнении эллипса предполагается ![]() ; отрезки
; отрезки ![]() называются большими полуосями, а отрезки
называются большими полуосями, а отрезки ![]() - малыми полуосями эллипса.
- малыми полуосями эллипса.
Определение Эксцентриситетом эллипса называется величина
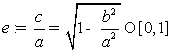 .
.
ЗАМЕЧАНИЕ 3 (геометрический смысл) Если ![]() при фиксированном
при фиксированном ![]() , то эллипс деформируется к окружности
, то эллипс деформируется к окружности ![]() . Если
. Если ![]() , то эллипс деформируется к отрезку
, то эллипс деформируется к отрезку ![]() .
.
Определение Прямая ![]() , проходящая через точку
, проходящая через точку ![]() кривой, называется касательной к кривой в этой точке, если расстояние от переменной точки кривой
кривой, называется касательной к кривой в этой точке, если расстояние от переменной точки кривой ![]() до прямой стремится к нулю быстрее, чем расстояние от нее до
до прямой стремится к нулю быстрее, чем расстояние от нее до ![]() , когда
, когда ![]() .
.
ЗАМЕЧАНИЕ 4 Уравнение касательной к эллипсу в точке ![]() имеет вид
имеет вид ![]() .
.
_____
Определение Гипербола – множество точек в ![]() , модуль разности расстояний от каждой из которых до двух заданных точек (фокусов) есть величина постоянная.
, модуль разности расстояний от каждой из которых до двух заданных точек (фокусов) есть величина постоянная.
ЗАМЕЧАНИЕ 1 Пусть модуль разности расстояний от текущей точки ![]() гиперболы до фокусов
гиперболы до фокусов ![]() равен
равен ![]() :
: ![]() .Тогда уравнение гиперболы (каноническое) имеет вид
.Тогда уравнение гиперболы (каноническое) имеет вид ![]() , где
, где ![]() .
.
Определение Прямая ![]() называется асимптотой неограниченной кривой, если расстояние от переменной точки кривой до этой прямой стремится к нулю, когда точка неограниченно удаляется по кривой.
называется асимптотой неограниченной кривой, если расстояние от переменной точки кривой до этой прямой стремится к нулю, когда точка неограниченно удаляется по кривой.
ЗАМЕЧАНИЕ 2 Прямые ![]() (Рис.2.13) являются асимптотами гиперболы при
(Рис.2.13) являются асимптотами гиперболы при ![]() .
.
Определение Отрезки ![]() называются вещественными полуосями, а отрезки
называются вещественными полуосями, а отрезки ![]() - мнимыми полуосями гиперболы. Точки
- мнимыми полуосями гиперболы. Точки ![]() называются вершинами гиперболы.
называются вершинами гиперболы.
Определение Эксцентриситетом гиперболы называется величина ![]() .
.
ЗАМЕЧАНИЕ 3 (геометрический смысл) Пусть ![]() фиксировано.
фиксировано.
а) Тогда ![]() , то есть тогда и только тогда, когда асимптоты проворачиваются вокруг начала координат к оси
, то есть тогда и только тогда, когда асимптоты проворачиваются вокруг начала координат к оси ![]() . При этом ветви гиперболы сжимаются к полуинтервалам
. При этом ветви гиперболы сжимаются к полуинтервалам ![]() , а их фокусы приближаются к вершинам. б)
, а их фокусы приближаются к вершинам. б) ![]() , то есть тогда и только тогда, когда асимптоты
, то есть тогда и только тогда, когда асимптоты
проворачиваются к оси ![]() . При этом ветви гиперболы разгибаются в вертикальные прямые
. При этом ветви гиперболы разгибаются в вертикальные прямые ![]() , а фокусы удаляются в бесконечность.
, а фокусы удаляются в бесконечность.
ЗАМЕЧАНИЕ 4 Уравнение касательной к гиперболе ![]() в точке
в точке ![]()
имеет вид ![]() .
.