Лекция 8. Потери давления в воздухопроводах
8.1. Сопротивление трения, коэффициент трения
Потерн давления на трение возникают по всей длине
воздухопровода и при данных его геометрических размерах и расходе воздуха
зависят от режима течения и состояния поверхности трения, т. е. шероховатости
стенок.
Потерю давления па трение в общем
виде можно найти по формуле:
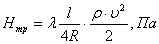 (24)
(24)
где 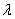 — коэффициент
трения; — коэффициент
трения;
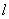 — длина
воздухопровода, м; — длина
воздухопровода, м;
R — гидравлический радиус поперечного сечении воздухопровода (отношение
площади поперечного сечения к периметру), м;
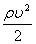 — динамическое давление потока, Па. — динамическое давление потока, Па.
Для круглого сечения воздухопровода
гидравлический радиус равен:
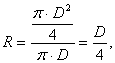 (25) (25)
где D- диаметр воздухопровода.
После подставки (25) в (24) расчетная формула примет вид:
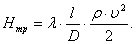
Для прямоугольного сечения со
сторонами а и b вводится понятие эквивалентного диаметра, равного:
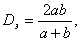
и потери давления рассчитывают по той
же формуле (26).
Воздухопроводы изготавливают из тонколистовой стали, черной или
оцинкованной, поверхность которой не является абсолютно гладкой. Таким
образом, внутренняя поверхность воздухопровода имеет микронеровности, которые
усиливают трение воздуха при течении.
Средняя высота выступов определяет собой величину абсолютной шероховатости
К, а отношение средней высоты выступов к диаметру воздухопровода D называется относительной
шероховатостью и обозначается
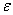 = K/D. = K/D.
В расчетных формулах обычно в качестве абсолютной
принимается гидравлическая
(эквивалентная) шероховатость, учитывающая не только высоту выступов, но также
их форму и расположение. Величину абсолютной шероховатости К для черной
кровельной стали принимают равной 0,02...0,04 мм, а для оцинкованной — 0,15 мм.
Режим течения потока внутри воздухопровода круглого сечения, в соответствии
с законами подобия, наиболее полно характеризуется критерием Рейнольдса,
определяемым выражением:
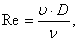
где 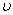 — средняя скорость потока воздуха, м/с; — средняя скорость потока воздуха, м/с;
D — диаметр, м;
v — кинематическая вязкость воздуха, м2/с.
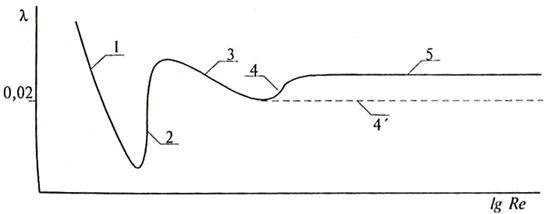
Если взять какой-либо воздухопровод с неизменной шероховатостью и
определить для него коэффициент трения 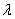 в зависимости
от изменения числа Рейнольдса, например при постоянном диаметре и за счет
увеличения скорости потока, полученную зависимость можно выразить в виде графика,
который представлен на рис. 11. в зависимости
от изменения числа Рейнольдса, например при постоянном диаметре и за счет
увеличения скорости потока, полученную зависимость можно выразить в виде графика,
который представлен на рис. 11.
При ламинарном течении (участок 1) при
увеличении числа Рейнольдса коэффициент трения уменьшается и может быть подсчитан по формуле:
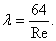
|
Рис. 11. Зависимость коэффициента X от числа Рейнольдса.
|
Если это значение 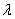 подставить в формулу
потерь напора на трение, получится следующее выражение: подставить в формулу
потерь напора на трение, получится следующее выражение:
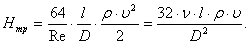 (27) (27)
Следовательно, при ламинарном режиме течения для воздухопроводов заданных геометрических размеров (D и 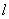 — const) и при неизменных физических константах потока ( — const) и при неизменных физических константах потока (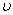 и и 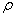 — const) потеря давления пропорциональна
первой степени изменения скорости потока. — const) потеря давления пропорциональна
первой степени изменения скорости потока.
При достижении критического числа Рейнойльдса (-2000...8000)
режим течения изменяется (участок 2) и переходит в турбулентный.
Когда пограничный ламинарный слой покрывает выступы шероховатости,
воздухопровод работает как гидравлически гладкий (участок 3) и коэффициент
трения 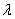 может быть
определен по формуле Блазиуса, имеющей вид: может быть
определен по формуле Блазиуса, имеющей вид:
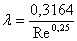
|
Если эту формулу подставить в уравнение потерь давления на
трение (26), получится выражение для определения этих потерь:
|
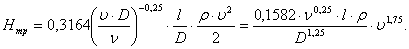 (28) (28)
При увеличении числа Рейнольдса толщина пограничного слоя
может стать меньше выступов шероховатости, в связи с чем возможно увеличение
коэффициента 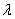 (участок 4).
Дальнейшее повышение числа Рейнольдса уменьшает толщину пограничного слоя,
выступы шероховатости почти полностью открываются, число Рейнольдса практически
не влияет на коэффициент (участок 4).
Дальнейшее повышение числа Рейнольдса уменьшает толщину пограничного слоя,
выступы шероховатости почти полностью открываются, число Рейнольдса практически
не влияет на коэффициент 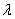 (участок
5) и воздухопровод работает как гидравлически шероховатый. Иногда
процесс идет по участку 4. (участок
5) и воздухопровод работает как гидравлически шероховатый. Иногда
процесс идет по участку 4.
Наиболее проста и удобна для приближенного расчета гидравлически
шероховатых труб формула Шифринсона:
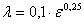 . .
В этом случае расчетная формула
принимает вид:
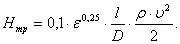 (29) (29)
Как видно, зависимость квадратичная
по скорости потока.
8.2. Потери давления в местных сопротивлениях, коэффициент местных сопротивлений
Фасонные части воздухопроводов (отводы, тройки, диффузоры,
конфузоры, внезапное расширение потока и т. д.) и оборудование, в которых
потери давления возникают при изменении скорости или направления движения
потока, называются местными сопротивлениями. Обычно в ВУ потери в местных
сопротивлениях превосходят потери давления на трение.
Коэффициентом местного сопротивления называется отношение потери
давления в местном сопротивлениии к динамическому давлению в данном сечении:
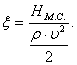 (30) (30)
Динамическое давление, к которому
относят коэффициент местного сопротивления, принимается для неменяющихся или
наиболее суженных поперечных сечений, но с обязательным указанием выбранного
места. Удобнее всего такое сечение брать в месте соединения с питающим воздухопроводом.
На практике при составлении таблиц и проведении расчетов
значения коэффициентов местных сопротивлений считают зависящими только от
соотношения геометрических размеров, а влиянием числа Рейнольдса и
шероховатости стенок пренебрегают.
Существенное влияние на значения коэффициента местного сопротивления
оказывает состояние входящего потока, обусловленное режимом течения, формой
входа, расположением вблизи других местных сопротивлений. Значения
коэффициентов местных сопротивлений, приводимые в справочной литературе, обычно
соответствуют наличию на входе равномерного поля скоростей воздушного потока.
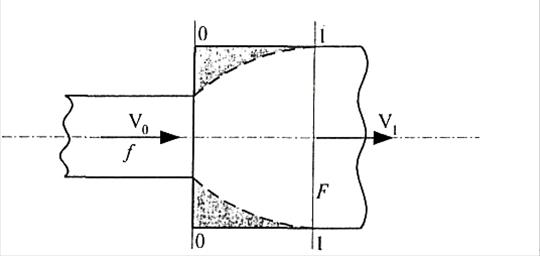
Лекция 8. Потери давления на внезапное расширение потока
Как правило, в местных сопротивлениях в том или другом сечениях скорость
потока изменяется. Это характерно для внезапного расширения потока, когда
образуется вихревая область (см. рис. 12). На ее образование расходуется
энергия, называемая потерей давления на удар.
Эту потерю можно определить аналитическим путем. Для сечений 0-0 и
1 - 1 напишем уравнение Бернулли:
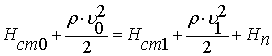
откуда потери давления между
сечениями 0-0 и 1-1 равны:
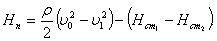
Применительно к объему, заключенному
между двумя этими сечениями, запишем уравнение импульса сил:
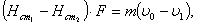
где 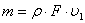 [кг/с] —
массовый расход воздуха, тогда: [кг/с] —
массовый расход воздуха, тогда:
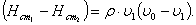

|
Рис. 12. Внезапное
расширение воздухопровода.
|
После
подстановки последнего уравнения в преобразованное уравнение Бернулли получим:
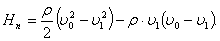
После упрощения формула для расчета
потерь примет следующий вид:
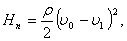 (31) (31)
т. е. потеря давления на удар равна
динамическому давлению потерянной скорости.
Коэффициент местного сопротивления % па удар при внезапном расширении
потока (относя его к динамическому давлению в узком сечении) равен:
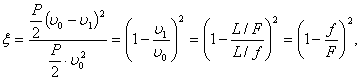 (32) (32)
где f и F— соответственно площади трубы в узком и широком
сечениях.
Для случаев выхода воздуха в
свободное пространства F = 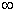 , , 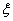 = 1 = 1
(L — объемный расход воздуха).
В общем
случае, когда изменение скорости происходит не внезапно, пользуются формулой:
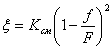 , ,
где К. — коэффициент смягчения, определяемый
опытным путем.
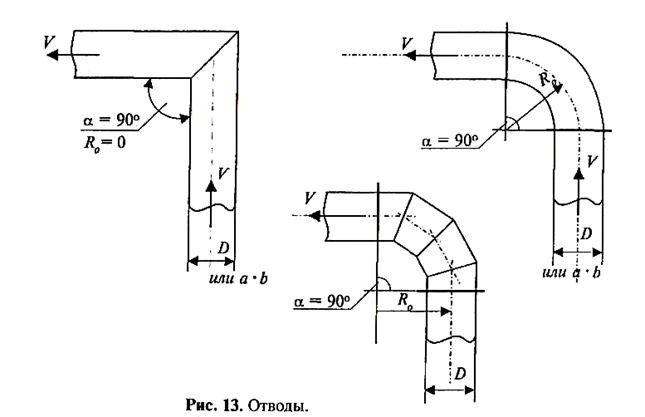
Потери давления в отводах
В отводах и коленах изменяется направление потока. Потери
давления в них возникают в результате интенсивного вихреобразования при отрыве
потока от стенок.
Изготавливают отводы из листовой
стали (рис. 13).
Сопротивление отвода складывается из
сопротивления на трение длины отвода, определяемой по формуле: 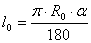 и прибавляемой к общей длине воздухопровода, и местного
сопротивления со своим коэффициентом и прибавляемой к общей длине воздухопровода, и местного
сопротивления со своим коэффициентом 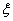 . .
Коэффициенты местных сопротивлений, отводов и колен находят по справочникам.
Например, шероховатый отвод из звеньев круглого сечения (наиболее часто
применяемый) имеет следующие значения коэффициентов местных сопротивлений 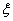 (см. табл. 3): (см. табл. 3):
Таблица
3
|
Угол отвода 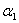 , град , град
,град
|
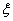
|
|
|
|
R, = 1,5•D
|
R, = 2 • D
|
|
30
|
|
0,08
|
0,07
|
|
60
|
|
0,14
|
0,12
|
|
90
|
|
0,18
|
0,15
|
Потери давления в тройниках
Фасонные части воздухопроводов, в которых происходит слияние
или разделение двух потоков, называются тройниками. Тройники с симметричным
расположением ответвлений называются штанообразными. Слияние и разделение трех
потоков происходит в крестовинах.
Тройники
бывают с круглым и прямоугольным поперечным сечением. Тройник состоит из
проходного патрубка и ответвления (рис. 14).
Коэффициенты местных сопротивлений(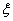 ) тройников даются на ответвление и на проход отдельно. ) тройников даются на ответвление и на проход отдельно.
Коэффициенты местных сопротивлений тройников могут иметь отрицательный
знак, что обусловлено эжекцией струй. Обычно
S = S6 + Sn;
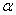 = 30° или 45°, в зависимости от
диаметров (S, Sб и Sn — соответственно площади сборного, бокового и проходного
сечений тройника). = 30° или 45°, в зависимости от
диаметров (S, Sб и Sn — соответственно площади сборного, бокового и проходного
сечений тройника).
Коэффициенты местного сопротивления проводника берутся из таблиц по
отношению площадей Sn/S, S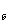 /S и расходов воздуха Qб/Q. /S и расходов воздуха Qб/Q.
Коэффициенты местных сопротивлений конфузоров и диффузоров находят из
таблиц по соотношениям геометрических размеров.
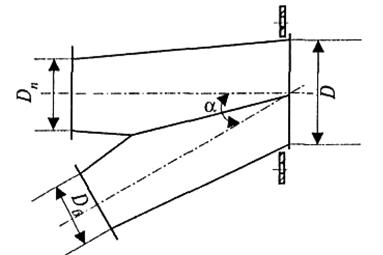
Рис.14 Тройник
|