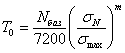Ременные передачи   

(Гузенков П.Г. $ 11.2 - 5c, 125-146)

Области применения, типы ремней, конструкции, основные параметры ременных передач. Общие сведения и основные характеристики. Разновидности и области применения.

Ременная передача является одной из древнейших. Она относится к передачам трением с гибкой связью. Применяется для передачи движения между валами, находящимися на значительном расстоянии один от другого (до 15 м). Мощность не превышает обычно 50 кВт.

В комбинации с зубчатой передачей ременную устанавливают обычно на быстроходную ступень как менее нагруженную.

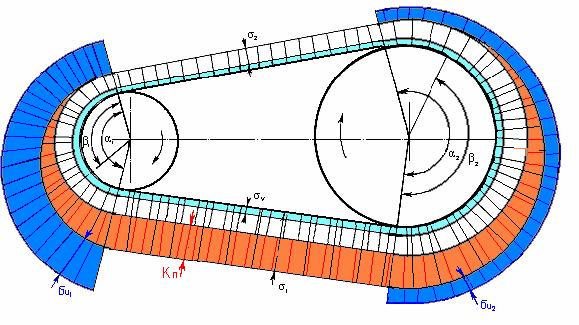
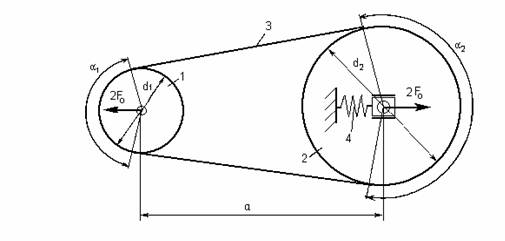
Ременная передача состоит из двух шкивов – ведущего 1, ведомого 2, и охватывающего их бесконечного ремня 3.

Для работы передачи необходимо предварительное натяжение ремня ( -F0 ), обеспечивающее на участках контакта ремень – шкив, обозначенных углами α1 и α2, возникновение сил трения.

В ременных передачах для создания и регулирования сил трения предусматривает натяжные устройства – 4.

Достоинства ременных передач

1.    Возможность передачи движения на значительном расстоянии

2.    Плавность и бесшумность работы

3.    Предохранение от перегрузок за счет проскальзывания ремня

4.    Простота конструкции и эксплуатации

Недостатки

1.    Повышенные габариты (для одинаковых условий диаметры шкивов примерно в 5 раз больше диаметров зубчатых колес)

2.    Непостоянство передаточного отношения, вызванное зависимостью скольжения ремня от нагрузки

3.    Повышенная нагрузка на валы и их опоры – в 2-3 раза по сравнению с зубчатой передачей

4.    Низкая долговечность ремней (в пределах от 1000 до 5000 ч)

5.    Пониженный коэффициент полезного действия. η = 0,96, передаваемая мощность менее 50 кВт.

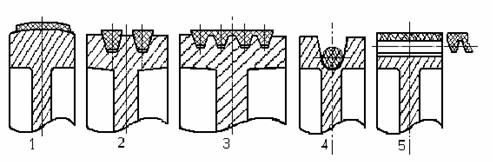
Классификация передач по типу ремней

1.    Плоскоременные

2.    Клиноременные

3.    Поликлиновые

4.    Круглоременные

5.    С зубчатыми ремнями

Общие требования к материалам приводных ремней

Ремень должен иметь: достаточную прочность при переменных напряжениях и износостойкость, достаточный коэффициент трения со шкивами во избежание больших сил начального натяжения, невысокую изгибную жесткость во избежание больших напряжений шкива при огибании шкивов.

Плоские ремни

Материалы ремней

1.    ГОСТ 18679-73 Кожаные ремни обладают хорошей тяговой способностью и высокой долговечностью, хорошо переносят колебания нагрузки. Из-за высокой стоимости в настоящее время применяются редко. V = 40…45 м/с, σ = 25 МПа

2.    ОСТ 38.05.98-76 Прорезиненные ремни. Основа ремня – прочная кордовая провулканизированная техническая ткань (2-9 слоев). Резина делает ремень монолитным и защищает ткань от истирания во время работы передачи. Прорезиненные ремни всех типов изготовляют как обкладок (для работы в нормальных условиях), так и с обкладками (для работы в сырых помещениях, а также в среде, насыщенной парами кислот и щелочей). V ≤ 30 м/с.

3.    ГОСТ 6982-75 Хлопчатобумажные ремни изготавливают на ткацких станках из хлопчатобумажной ткани в несколько переплетающихся слоев (4-8) с последующей пропиткой азотокеритом (горный воск) и битумом. Применяют в быстроходных передачах, преимущественно для малых мощностей при V ≤ 20 м/с.

4.    Шерстяные ремни изготавливают из шерстяной пряжи, переплетенной и прошитой хлопчатобумажной пряжей, пропитанной составом олифы, мела и железного сурика. σ = 30,0 МПа. Применяют для средних и даже больших мощностей. Характеризуется значительной упругостью и потому хорошо работают при неравномерной и ударной нагрузке. Они менее чувствительны к влаге, парам кислот, щелочей и т. п. Находят применения в химической промышленности.

5.    Ремни из синтетических материалов. Полиамидные ремни. V ≤ 100 м/с. Передают мощность до тысяч кВт. Ремни ткут из полиамидных нитей, либо получают в виде пленочной многослойной ленты армированной металлическими канатиками.

Клиновые ремни

Это ремни трапециевидного сечения с боковыми рабочими сторонами, работающие на шкивах с канавками соответствующего профиля.

Клиновая форма ремня увеличивает его сцепление со шкивом примерно в 3 раза. Рабочими являются боковые поверхности ремня. Реализация заклинивания осуществляется за счет формы канавки шкива, которую выполняют так, чтобы между ее основанием и ремнем был зазор Δ.

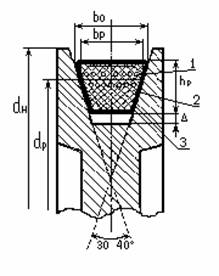
В то же время ремень не должен выступать за пределы наружного диаметра шкива, так как в этом случае кромки канавок быстро разрушают ремень.

Расчетным диаметром dp шкива является диаметр окружности расположения центров тяжести поперечных сечений ремня или нейтрального слоя при изгибе – ширина bp.

По стандарту на размеры шкивов клиноременных передач канавки изготавливают с углами 30º .. 40º. В целях выравнивания давления углы канавок делают меньше угла профиля ремня: чем меньше диаметр шкива, тем меньше угол канавки (неравномерность распределения давления объясняется деформацией слоев ремня при изгибе).

Одно из типичных и наиболее распространенных сечений клинового ремня представлено на рисунке. Слои шнурового (или тканного) корда 1 являются основным несущим элементом ремня. Они расположены в зоне нейтрального слоя bp для повышения гибкости ремня. Тканевая обертка увеличивает прочность ремня и предохраняет его от износа. Резина 2, как заполнитель, объединяет ремень в единое целое и придает ему эластичность.

Клиновые ремни изготавливают в виде замкнутой бесконечной ленты. Для передач общего назначения по ГОСТ 1284.1-80 изготавливают семь типов клиновых ремней 0, А, Б, В, Г, Д, Е, отличающиеся размерами поперечного сечения. Размеры сечения соответственно увеличивают от типа 0 к Е.

Число клиновых ремней принимают от 3 до 5 (максимальное – 8).

Передаточное число для одноступенчатой клиноременной передачи U ≤ 8.

К. П. Д. - η = 0,95 .. 0,96.

Стандартом предусмотрено три разновидности клиновидных ремней:

ГОСТ 12841-80 – нормального сечения

ГОСТ 12842-80 – узкие

ГОСТ 12843-80 – широкие вариаторные

Передача зубчатыми ремнями

В этой передаче на внутренней стороне плоского ремня образованы поперечные выступы (зубья) трапецеидальной формы, а на шкиве – соответствующие впадины. Таким образом передача работает по принципу зацепления, а не трения. К ременным передачам она относится условно только по названию и конструкции тягового органа. По принципу работы она ближе к цепным передачам. Принцип зацепления устраняет скольжение и необходимость в большом предварительном натяжении, что повышает К. П. Д. передачи. Использование принципа зубчатого ремня предложено давно, но его практическое применение оказалось возможным только с появлением новых материалов – пластмасс. Ремень изготавливают из пластичной малостойкой резины или пластмассы и армируют стальными проволочными тросами полиамидным кордом.

Зубчатые ремни применяют при скоростях V ≤ 50 м/с,

передаточных числах U ≤ 12 ( ≤ 20) и мощностях до 100 кВт.

Поликлиновые ремни

Имеют продольные клиновые выступы на внутренней стороне и выполняются бесконечными. В плоской части ремня размещается кордшнур, воспринимающий передаваемую нагрузку. Эти ремни сочетают достоинства клиновых ремней (повышенное сцепление со шкивом) и гибкость, характерную для плоских ремней, вследствие чего минимальный диаметр малого шкива можно назначить меньшим, а передаточное число увеличить до U ≤ 15.

Круглые ремни

Применяют по одному в передаче. Диаметры ремней 3-12 мм. Профиль канавок шкива – полукруглый или трапециевидный c < 40º.

Материал: кожа, капрон, х/б нить.

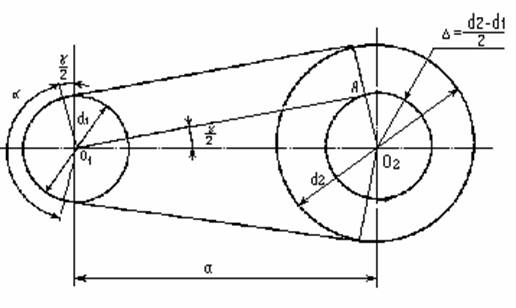
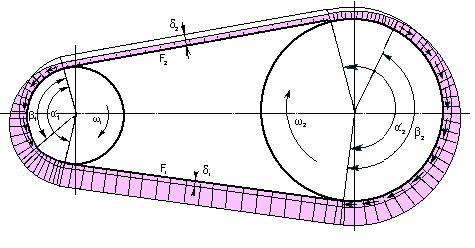
Основные геометрические соотношения элементов конструкции и кинематика ременных передач

При проектировании ременных передач рассчитывают следующие геометрические параметры:

γ – угол между ветвями ремня;

α – угол обхвата на малом шкиве;

L – длина ремня;

а – межосевое расстояние (при использовании бесконечных ремней);

Угол между ветвями передачи определяют из вспомогательного треугольника О1АО2.

, где ;

Отсюда угол между ветвями ремня

(рад)

Угол обхвата на малом шкиве

Для клиноременной передачи

Для плоскоременной

Длина ремня (без учета провисания и начального деформирования)

Пользуясь приближенной зависимостью , подставляя значения γ и заменяя   на dcp получим:

Расстояние между осями шкивов при выбранной длине ремня

   .

При расчетах длин ремней и межосевых расстояний клиноременных передач оперируют расчетными диаметрами шкивов по нейтральному слою ремня.

Оптимальное межосевое расстояние

Минимальное межосевое расстояние

, где h – высота сечения ремня

Критерии работоспособности и расчета ременных передач. Работа ремня на шкивах

(Теория Жуковского Н. Е., Петрова Н. П.)

Основные критерии расчета ременных передач:

1.    Тяговая способность или прочность сцепления ремня со шкивом;

2.    Долговечность ремня.

В наше время основным является расчет ременных передач по тяговой способности.

Ремни существующих конструкций, рассчитанные по тяговой способности, в обычных условиях эксплуатации обеспечивают минимально необходимую долговечность.

Скольжение в ременной передаче

Работа упругого ремня связана с упругим скольжением по шкивам. Это явление возникает из-за различного натяжения ведущей и ведомой ветвей ремня.

При обходе ремнем ведущего шкива натяжение его падает. Ремень укорачивается и проскальзывает по шкиву. На ведомом шкиве ремень удлиняется и опережает шкив. Скольжение происходит не по всей дуге обхвата α1,2, а на некоторой части ее – β, называемой дугой скольжения.

Сила трения между ремнем и шкивом передается в основном на дуге скольжения, но частично благодаря тангенциальной податливости ремня также на дуге покоя. В обычных расчетах передачу силы трения на дуге покоя не учитывают. Дуга скольжения расположена со стороны сбегания ремня со шкива.

Со стороны набегания ремня находится дуга покоя, т. е. постоянного сцепления ремня со шкивом. Окружная скорость каждого шкива равна скорости набегающей ветви ремня.

При холостом ходе упругое скольжение и дуга скольжения равны нулю. По мере роста нагрузки дуга скольжения растет. Когда она достигает всей дуги обхвата, начинается буксование передачи.

Согласно условию постоянства массы ремня, пробегающего в единицу времени через данное неподвижное сечение, относительное скольжение ремня равно разности относительных удлинений ε1 – ведущей и ε2 – ведомой ветвей ремня:

(кси) ;         ;   ; (закон Гука)

Окружные скорости на шкивах

;      (м/с)

где d1 и d2 – диаметры ведущего и ведомого шкивов (м)

 (мм)

ГОСТ 1284.3-80

n1 и n2 – частоты вращения ведущего и ведомого шкивов (об/мин).

Вследствие упругого скольжения окружная скорость на ведомом шкиве V2 меньше скорости V1 на ведущем.

Передаточное число

.

Основные теории расчета ременных передач. Усилия и напряжения в ремнях, кривые скольжения и допускаемые полезные напряжения

Для создания необходимого трения между ремнем и ободом шкива ремень должен иметь достаточное натяжение F0.

Оно достигается предварительным натяжением ремня при монтаже или с помощью подвижной опоры. Чем больше F0, тем выше тяговая способность передачи. Но при большой величине начального натяжения F0 ремень получает большую вытяжку и снижается его долговечность. Поэтому F0 выбирают таким, чтобы ремень мог сохранить это натяжение достаточно длительное время, не получая большой вытяжки.

Начальную систему натяжения ремня определяют по формуле:

F0 = A∙σ0

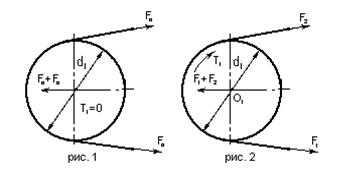
где А – площадь поперечного сечения ремня;

σ0 – начальное напряжение в ремне

Приближенно, в состоянии покоя и при холостом ходе каждая ветвь натянута одним и тем же усилием - F0 (см. рис. 1)

   C приложением момента Т1 (рис. 2) ведущая ветвь натягивается до усилия F1, натяжение ведомой ветви уменьшается до F2.

Силы натяжения F1 и F2 можно определить из условия равновесия шкива ∑М0 = 0

 или  

Из условия постоянства геометрической длины ремня удлинение ведущей ветви компенсируется сокращением длины ведомой ветви.

F1 = F0 + ΔF, F2 = F0 – ΔF

Так как сумма сил натяжения ветвей постоянна (независима от нагружения передачи) то

 ‚

Складывая и вычитая выражения  и ‚ получим

,     

Тяговая способность ременной передачи

Тяговая способность ременной передачи зависит от соотношений F1 и F2 на границе буксования. Мощность зависит от силы трения между ремнем и шкивом. Эту зависимость установил Л. Эйлер (1775 г.).

Зависимость выведена без учета центробежных сил для нерастяжимой нити, скользящей по цилиндру.

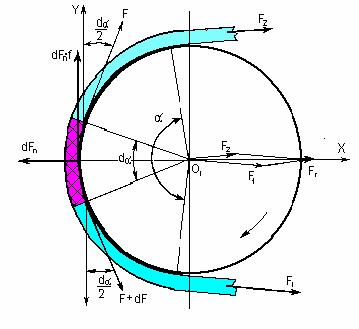
Рассмотрим условия равновесия гибкой нерастяжимой нити, охватывающей негладкий барабан.

Выделим элементарный участок ремня с центральным углом dα. Нормальная сила, действующая на элемент ремня со стороны шкива – Fn. Составим уравнение ∑Х = 0

 и ∑Y = 0

Принимаем:;

При

,    ,

После интегрирования о дуге скольжения и подстановки пределов S1 и S2 от 0 до α→β

,  получаем

 _{- формула Эйлера,   где е = 2,71828}

f – коэффициент трения между ремнем и ободом шкива;

β – угол скольжения; принимают ≈ 0,7 α

Решая систему уравнений получим

,   ,         , 

При         начинается буксование ремня

Распределение сил в ременной передаче

Натяжение ремня от центробежной силы

При работе передачи возникает дополнительное натяжение Fv, которое отбрасывает ремень от шкива

где ρ – плотность, кг/м³

А – площадь сечения ремня, м²

V – окружная скорость, м/с

1. С учетом центробежной силы натяжение ремня на  без нагрузки – на холостом ходу:

3. Под нагрузкой

Ведущая ветвь (набегающая на ведущий шкив) 

Ведомая ветвь (сбегающая с ведущего шкива) 

Нагрузку на валы и опоры Fr определяют как равнодействующую от сил F1 и F2 из параллелограмма сил.

.

Силу Fr можно выразить через Ft

Fr ≈ 2,5Ft – для прорезиненных и кожаных ремней;

Fr ≈ 3Ft – для хлопчатобумажных ремней;

Fr ≈ 4Ft – для шерстяных;

Нагрузка на валы в 2,5-4 раза превышает передаваемое окружное усилие – недостаток ременной передачи.

Напряжения в ремне

При работе ременной передачи напряжения в различных сечениях по длине ремня неодинаковы. Различают следующие виды напряжения в ремне.

1.     Начальное напряжение σ0, определяется в зависимости от величины начальной силы натяжения ремня:

, где А – площадь поперечного сечения ремня.

Для стандартных ремней рекомендуется принимать:

σ0 = 1,76 МПа – для плоских ремней;

σ0 = 1,2 .. 1,5 МПа – для клиновых ремней;

σ0 = 3 .. 4 МПа – для полиамидных ремней;

Для удобства построения эпюры напряжений в ремне изобразим вначале действие на ремень центробежных сил.

2.     Напряжение от центробежных сил. Величина этого напряжение зависит от силы Fv и определяется как , где ρ – плотность ремней 0,9 .. 1,2 г/см³

σv – распределяется по всей длине равномерно

3.     До приложения нагрузки усилие предварительного напряжения ремня, также как и Fv распределяется по длине ремня равномерно.

После приложения нагрузки усилие предварительного натяжения ремня, также как и Fv распределяется по длине ремня равномерно.

После приложения нагрузки ведущая ветвь натягивается силой , а ведомая . При этом в ведомой ветви возникает напряжение ; в ведущей ветви .

Полезное напряжение, зависящее от передаваемого ремнем окружного усилия Ft, можно определить как разность напряжений σ1 и σ2

Кn = σ1 – σ2

Кn на участках скольжения ведущего и ведомого шкивов изменяется от σ1 до σ2

4.     Напряжение изгиба σu, возникающее в сечениях ремня при огибании шкивов и изменяющееся по пульсирующему циклу. Наружные слои ремня при огибании шкива удлиняются, а внутренние – сжимаются. Приближенно примем, что закон Гука справедлив и для материалов ремней, тогда для выпуклой стороны ремня

 или

где E – модуль продольной упругости ремня

δ – толщина ремня

На шкиве меньшего диаметра напряжения изгиба больше. σu является основной причиной усталостного разрушения ремня и не влияет на его тяговую способность.

5.     Наибольшее суммарное напряжение

В ведомой ветви минимальное напряжение

Как показывает эпюра суммарных напряжений в ремне, в местах набегания ремней на шкивы и сбегания ремней не происходит резких скачков напряжений, так как ремни постепенно меняют радиусы кривизны.

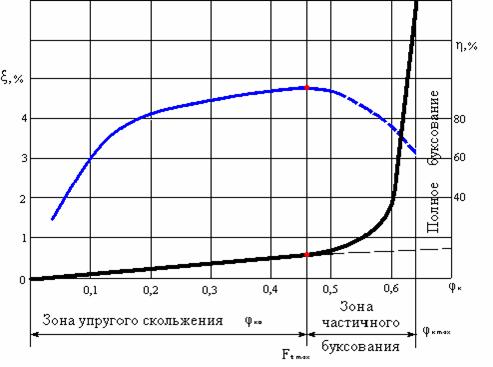
Коэффициент тяги и кривые скольжения

В результате исследования кривых скольжения, построенных по опытным данным, установлена связь между полезной нагрузкой (окружным усилием Ft) и предварительным натяжением ремня F0 в зависимости от относительного скольжения ремня – ξ.

Отношение передаваемого ремнем окружного усилия к сумме натяжений его ветвей называют коэффициентом тяги.

Коэффициент тяги характеризует нагрузочную способность передачи.

На графике по оси абсцисс отложен коэффициент тяги φк, по оси ординат коэффициент скольжения ξ и К. П. Д. передачи. На начальном участке кривой скольжения от 0 до φк0 наблюдается только упругое скольжение. Этот участок близок к прямой. Здесь К. П. Д. и ξ

падают с умень-шением нагрузки. Дальнейшее увеличение нагрузки (т. е. увеличение φк) приводит к буксованию. В зоне частичного буксования (от φк0 до φк max) наблюдается как упругое скольжение так и буксование. Рабочую нагрузку следует принимать при φк < φк0, в пределах, которые соответствуют наибольшему значению К. П. Д.

Работа в зоне частичного буксования допускается только при пуске (т. е. при кратковременных нагрузках).

 – коэффициент запаса сцепления

Допускается величина β для ремней: плоских, кожаных, шерстяных 1,35 .. 1,5;

прорезиненных                        1,15 .. 1,3;

хлопчатобумажных                  1,25 .. 1,4

клиновых                            1,5 .. 1,6

Допускаемые напряжения в ремне

График показывает, что оптимальная величина коэффициента тяги φк0 определяет максимальное полезное усилие тяги Ft max, т. е.

Преобразуя эту формулу получим:

 или

где  - допускаемое приведенное полезное напряжение в ремне, соответствующее коэффициенту тяги φк0. значения [K]0 дают в таблицах.

Допускаемое расчетное напряжение в ремне [K]n используют при проектировании ременных передач. Экспериментальным путем установлено, что

где Kα – учитывает влияние угла обхвата малого шкива;

KB – вид передачи и расположение ее элементов;

Kv – ослабление сцепления ремня под действием центробежной силы (скоростной коэффициент).

Окончательно полезная сила и Ft мощность N передаваемые ремнем

;     

где Kd – коэффициент динамической нагрузки

Расчет по тяговой способности

Методика расчета плоскоременных передач сводится к определению расчетной площади сечения ремня

Для клиноременной передачи – в определении требуемого числа клиновых ремней – Z (наибольшее число)

.

При большем количестве ремней из-за деформации изгиба валов увеличивается неравномерность распределения нагрузки между валами.

Расчет ремней на долговечность

Ремни являются наименее долговечными элементами машин. В настоящее время нет строгой методики расчета ремней на долговечность. В связи с этим для расчетов на долговечность ограничиваются поправками к расчетам по тяговой способности и проверкой частоты пробегов ремня в секунду.

где V – скорость ремня м/с, L – длина ремня, м

Для ремней справедливо известное уравнение кривой усталости

где σmax – максимальное напряжение цикла

N – общее число циклов нагружения ремня до разрушения (при переменном режиме и в передачах с U ≠ 1 – эквивалентное число циклов)

m – показатель степени

         для плоских ремней                 m = 5 .. 6

         для клиновых ремней      m = 6 .. 11

При передаточном числе U = 1 и постоянном режиме нагружения N = 3600∙Пz∙Zш∙T,

где Zш – число шкивов

T – ресурс ремня в часах

Переменность режима и отличие U от 1 учитывается коэффициентами.

, Т0 – из таблиц, U – передаточное число

К. П. Д. ременных передач

Потери мощности в ременной передаче имеют место в опорах валов, при огибании ремнем шкивов (на деформацию изгиба) при скольжении ремня по шкивам (нагрев износ) и потери от сопротивления воздуха движению ремня и шкивов.

Все эти потери не поддаются точному расчету, поэтому К. П. Д. ременных передач определяются экспериментально.

Среднее значение К. П. Д.

для плоскоременных передач        η = 0,97

для клиноременных передач         η = 0,99
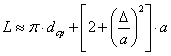
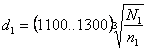
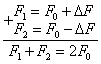
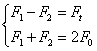
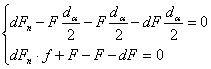
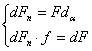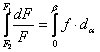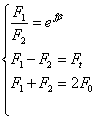