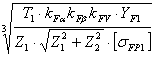|
|
Выберете лекцию |
Передачи зацеплением
Передачи трением
КОНИЧЕСКИЕ
ЗУБЧАТЫЕ ПЕРЕДАЧИ
Конструктивные особенности, геометрия,
силы в зацеплении, расчет на выносливость. Иванов
М.Н. «Детали машин» 1984г. §8.8 с. 129 -135. Гузенков
П.Г. «Детали машин» 1986г. §12.2 с. 164,196-198. Иосилевич Г.Б. «Детали машин» 1988г. §14.4,14.7
с. 173.
Рис.1
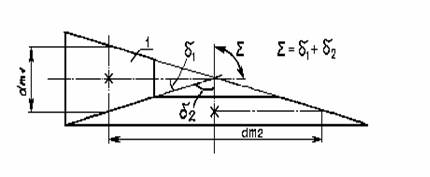
В подавляющем большинстве случаев Σ = 90е.
Другие углы применяются редко, т.к. усложняется технология изготовления
корпусов, в которые устанавливаются валы передачи со своими подшипниками.
Следует подчеркнуть, что произвольный выбор угла Σ не приводит к усложнению или удорожанию
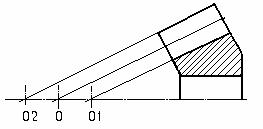
изготовления самих зубчатых колес. На рис.1 показаны основные кинематические параметры
конической зубчатой передачи. δ1 и δ2 - Углы делительных конусов шестерни и колеса Σ = δ1 +
δ2
Передаточное число
конической зубчатой передачи при любом угле Σ. U
= При угле Σ =
90° передаточное число может быть
определено помимо указанных зависимостей как U = tg δ2
= ctg δ1
2. Виды конических зубчатых передач. Существует более десяти разновидностей
конических зубчатых передач, из которых наиболее распространенными являются три: - коническая
зубчатая передача с прямыми зубьями, - коническая
зубчатая передача с тангенциальными зубьями, -
коническая зубчатая передача с круговыми
зубьями, образованные зубчатыми колесами с соответствующими
разновидностями зубьев.
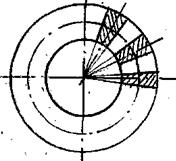
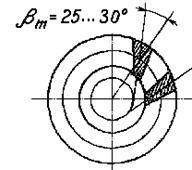
конуса являются
прямые, касательные к концентрической окружности / Рис. 3./
Углы
наклона линий зубьев не прямозубых конических колес определяются как показано
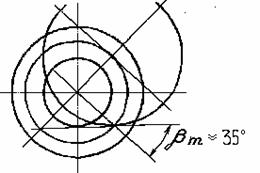
на рис. 3 и 4. βm – средний угол
наклона линии зуба на делительном конусе, который измеряется как острый угол
между касательной к поверхности зуба в средней точке и радиусом, проходящим
через эту точку. Направление зубьев не
прямозубых конических колес определяется, если смотреть со стороны вершин
делительного конуса. На рис. З и 4 показаны колеса с левым направлением зуба.
3. Недостатки конических зубчатых передач по
сравнению с цилиндрическими: - сложность
изготовления. Кроме допусков на изготовление зубчатых венцов здесь необходимо
выдерживать допуски на углы Σ
, δ1,
δ2, - затрудненность размещения опор валов. Одно из
колес обычно располагается консольно, - неравномерность распределения нагрузки по
длине зуба, более высокая концентрация нагрузки из-за консольного расположения
колес, - наличие осевой составляющей усилия
зацепления, что вызывает нагружение опор осевыми силами. Некоторые из
отмеченных недостатков приводят к снижению нагрузочной способности конической
передачи по сравнению с эквивалентной цилиндрической передачей. По
экспериментальным данным нагрузочная способность конической прямозубой передачи
не превышает 0,85 от нагрузочной способности эквивалентной цилиндрической
прямозубой передачи. Стандарты на Зубчатые конические передачи
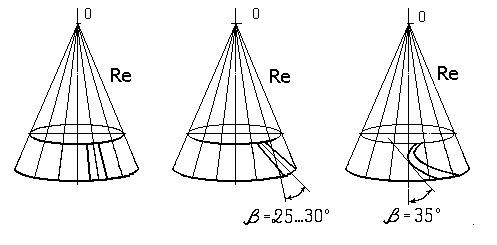
4. Осевые формы зубьев. По ГОСТ 19325-73 различают
три осевые формы зубьев конических колес.
Вершины конусов
делительного и впадин не совпадают. Применяют для колес с
тангенциальными и круговыми
зубьями /основная форма массового производства/.
Применяют
только для колес с круговыми зубьями. Не основная форма, применяется при
индивидуальном и мелкосерийном производстве. 4. Основные
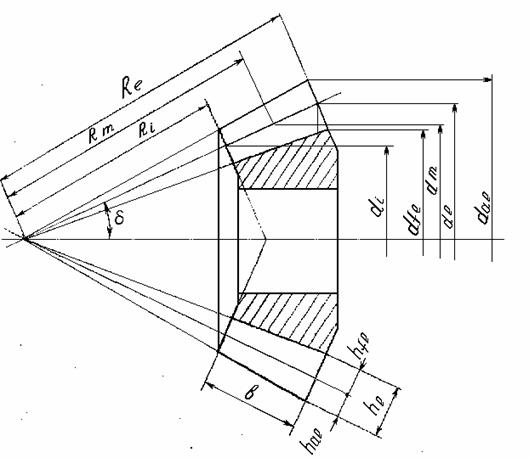
геометрические параметры
Рис.7 Индексы
параметров Конусы: i
– внутренний ; m
– средний; e
– внешний; a – окружность конуса вершин; f – окружность конуса
впадин. d – диаметры
делительных окружностей. ha - высота головки зуба;
hf
– высота ножки зуба. R – конусные
расстояния. Параметры зубчатой передачи mnm – средний модуль в сечении, нормальном к теоретической линии зуба; mte – внешний окружной
модуль. Rm = Re – 0,5 b.
Kbe – коэффициент
ширины зубчатого вена Kbe ≤ 0,3.
mnm = mte (1 – 0,5Kbe). de = mte٠Z ; hae
= mte; hfe = 1,2mte; dae = de + 2hae٠Cosδ; dfe = de - 2hfe٠Cosδ. 6. Силы в зацеплении, эквивалентное колесо.
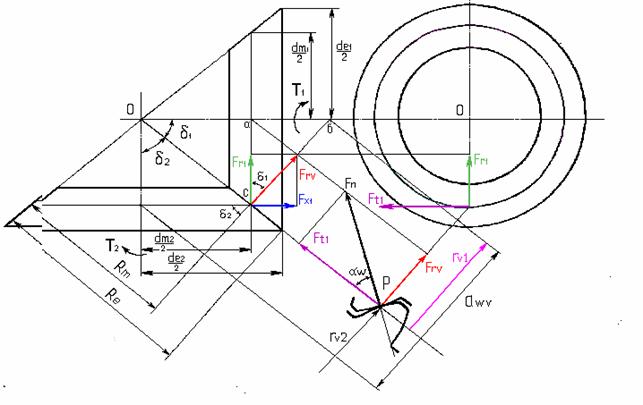
Ft = Fx2 = Fr1 = Frv٠Cosδ1 ; Fx2 = Fr1 = Ft٠tgα ٠Cosδ1 Fx1 = Fr2 = Frv٠Sinδ1 ; Fx1 = Fr2 = Ft٠tgα ٠Sinδ1. РАСЧЕТЫ
НА ПРОЧНОСТЬ
1. ПОНЯТИЕ ЭКВИВАЛЕНТНОЙ
ПЕРЕДАЧИ И ЭКВИВАЛЕНТНОГО КОЛЕСА ПАРАМЕТРЫ
ЭКВИВАЛЕНТНОй ПЕРЕДАЧИ. При расчетах на прочность прямозубых конических передач
используется методика ГОСТ 21354-75 для цилиндрических передач. Для этого вместо прямозубой конической передачи вводят в рассмотрение
эквивалентную цилиндрическую прямозубую передачу, состоящую из эквивалентных
цилиндрических зубчатых колес (Рис. 8 ), которые имеют в полюсе зацепления
шаги, размеры и форму зубьев, идентичные размерам и форме зубьев колес данной
передачи в сечении их дополнительным конусом через середину зубчатого венца. Кинематические
и геометрические параметры эквивалентной передача выражаются через аналогичные
параметры данной передачи и затем вводятся в расчетные формулы. Таким образом,
рассчитывается не данная , а эквивалентная передача» но результаты расчетов
переносятся на данную коническую зубчатую передачу. Определим
параметры эквивалентной передачи / Рис. 6 /: r v - радиус начальной/
делительной/ окружности эквивалентного колеса, Z v – число зубьев
эквивалентного колеса, U v – передаточное число эквивалентной передачи, a v – межосевое
расстояние эквивалентной передачи, T v – крутящий момент на валу эквивалентного колеса. Исходная формула из
теории расчета цилиндрической зубчатой передачи с учетом пониженной несущей
способности конической передачи σ
нр2 = ZM ٠ZH ٠Zε ٠ Найдем зависимости
между реальными и эквивалентными параметрами зубчатой передачи. rv1, rv2 ; Zv; Uv
; av ; Tv1 ; Tv2 . Определяем радиусы эквивалентных
цилиндрических колес: rv1 = dv2 = 2·rv2
= Число
зубьев колес эквивалентной передачи: mnm·Z v = Передаточное число эквивалентной
прямозубой передачи: Uv = Межосевое расстояние:
av
= rv1 + rv2 = Крутящие моменты эквивалентной передачи: Tv2 = rv · Ft2
= Ft2 · Tv2 = Tv1· Uv
= Tv2= T2·
Tv1 = T1· b = Re·Kbe
, Rm = Re – 0,5·b = Re(1–
0,5·Kbe). Полученные
зависимости подставляем в формулу (1) и производим преобразования для придания
расчетной формуле типового вида. σнр2
= ZM· ZH· Zε· σнр2
= ZM· ZH·Zε· σнр2
= ZM· ZH· Zε·
Re = Для прямозубых передач
KR =
|
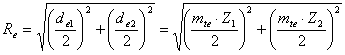 ,
,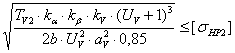 .
.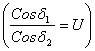
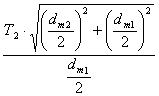
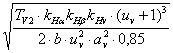 ≤ [σ
≤ [σ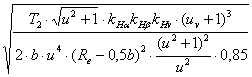 ≤ [σ
≤ [σ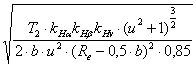 ≤ [σ
≤ [σ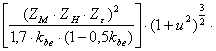 ·
·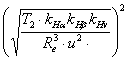
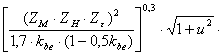 ·
·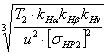
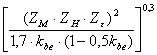 =
=