Выберете лекцию

Передачи зацеплением

Зубчатые

Цилиндрические прямозубые

Цилиндрические косозубые

Конические

Червячные

Волновые

Цепные

Передачи трением

Фрикционные

Ременные

Вариаторы

ЗУБЧАТЫЕ ПЕРЕДАЧИ. ОБЩИЕ СВЕДЕНИЯ

Назначение зубчатых передач. Классификация и область применения. Положительные и отрицательные качества.

Иванов М.Н. «Детали машин» 1984г. §8.2 с. 101-102.

Гузенков П.Г. «Детали машин» 1986г. §12.1 с. 153-155.

Иосилевич Г.Б. «Детали машин» 1988г. §14.1 с. 159-160.

ГОСТ 16530–70. Зубчатая передача – трехзвенный механизм, в которм два подвижных звена являются зубчатыми колесами, образующими с неподвижным звеном вращательные или поступательные пары.

Зубчатые передачи применяются для передачи вращательного движения между двумя валами.

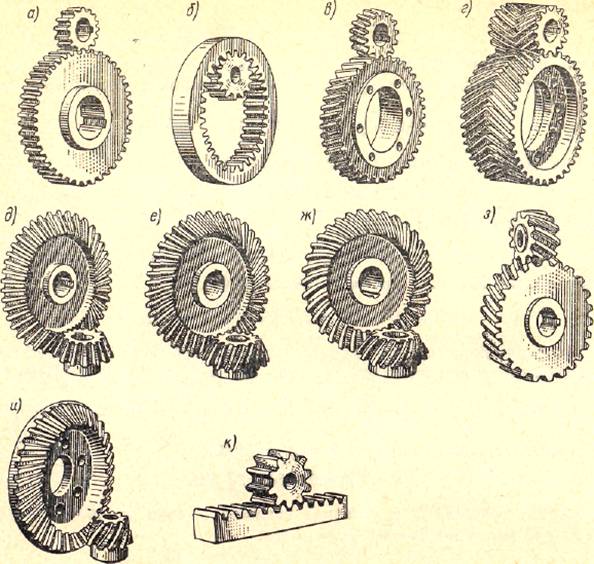
Простейшая зубчатая передача состоит из двух колес с зубьями, посредством которых они сцепляются между собой (рис. 1, а..м). Вращение ведущего зубчатого колеса преобразуется во вращение ведомого колеса путем нажатия зубьев первого на зубья второго. Меньшее зубчатое колесо передачи называется шестерней, большее – колесом.

Классификация

Зубчатые передачи могут преобразовывать вращательное движение между валами с параллельными (рис. 1, а... г), пересекающимися (рис. 1,д...ж) и перекрещивающимися (рис. 1,з,и) геометрическими осями. Угол между геометрическими осями валов конических и винтовых передач может быть в пределах 0...180⁰, но обычно этот угол равен 90°. В гипоидной передаче угол скрещивания валов принимают равным 90°.

По форме образующей поверхности для нарезания зубьев различают цилиндрические (рис. 1,а...г,з), конические (рис. 1,д...ж,и), эллиптические, фигурные зубчатые колеса и с неполным числом зубьев. В курсе «Детали машин» изучают только широко распространенные зубчатые колеса круглой формы, т. е. цилиндрические и конические; остальные зубчатые колеса, встречающиеся очень редко, рассматривают в специальных курсах.

По форме и расположению зубьев относительно образующей поверхности заготовки различают прямые (рис. 12.1,а, б, о), косые (рис. 1,6, е,з, и), шевронные (рис. 1,г), а также круговые (рис. 1, ж) и другие криволинейные зубья.

В зависимости от взаимного расположения валов передачи формы зубчатых колес и формы зубьев передачи бывают: цилиндрические — прямозубые (рис. 1, а, б), косозубые (рис. 1,6) и шевронные (рис. 1,г); конические — прямозубые (рис. 1,д), с тангенциальными зубьями или косозубые (рис. 1, е) и с круговыми зубьями (рис. 1, ж); винтовые (рис. 1,3), состоящие из двух цилиндрических косозубых колес, установленных на перекрещивающихся валах; гипоидные или конические винтовые (рис. 1,и), состоящие из двух конических косозубых или с криволинейными зубьями колес, которые установлены на перекрещивающихся валах.

В зависимости от взаимного расположения зубчатых колес различают зубчатые передачи с внешним (рис. 1, а) и внутренним зацеплением (рис. 1,6). В последней, в отличие от первой зубчатые колеса вращаются в одну сторону.

Разновидностью зубчатой передачи служит реечная передача

(рис. 1, к), преобразующая вращательное движение шестерни в возвратно-поступательное движение рейки или наоборот. Рейку рассматривают как зубчатое колесо бесконечно большого диаметра.

Рис. 1 (На доске изобразить в виде кинематических схем)

Зубчатые передачи применяют не только в виде пары зубчатых колес, но и в более сложных сочетаниях, образующих многоступенчатые зубчатые передачи, а также в виде планетарных передач , состоящих из зубчатых колес с перемещающимися геометрическими осями, когда оси одного или нескольких колес подвижны.

По относительному расположению поверхностей вершин и впадин зубьев колес различают: передачи внешнего зацепления {образуются при зацеплении колес с внешними зубьями) и передачи внутреннего зацепления (образуются при зацеплении колес, одно из которых имеет внутренние зубья, а другое — внешние зубья, рис. 1, б).

По профилям зубьев колес передачи подразделяют: на передачи с эвольвентным зацеплением, в котором профили зубьев очерчены эвольвентами окружностей; на передачи с циклоидальным зацеплением, в котором профили зубьев очерчены по эпи- и гипоциклоидам; на передачи с зацеплением Новикова, в котором взаимодействуют выпуклый профиль зуба одного колеса и вогнутый профиль зуба другого колеса.

Передачи с эвольвентным зацеплением имеют наиболее широкое применение благодаря тому, что зубья могут быть обработаны инструментом с прямолинейной режущей кромкой (поэтому их легче изготовить с высокой точностью), а также нечувствительности к отклонениям межосевого расстояния (поэтому не изменяется закон движения и передаточное отношение).

В зависимости от назначения зубчатые передачи могут встраиваться в конструкцию машины (встроенные передачи) или выделяться в самостоятельный узел (агрегат) и иметь отдельный корпус.

По окружной скорости – V_t – тихоходные (до 3м/с) среднескоростные

( 3 – 15 м/с), быстроходные (свыше 15 м/с ).

По конструктивному исполнению передачи могут располагаться вне корпуса и иметь легкое ограждение (открытые передачи) либо работать в корпусе, изолирующем их от внешней среды (закрытые передачи). Открытые передачи работают без смазывания или при

периодическом смазывании при небольших окружных скоростях (тихоходные, передачи). Закрытыми выполняют обычно передачи, работающие при средних и высоких окружных скоростях (быстроходные передачи) с обильным смазыванием (из масляной ванны, струей масла и др.).

Различают силовые и несиловые (кинематические) передачи. Силовые передачи используют для передачи мощностей, и их габариты определяются как правило, прочностной надежностью.

Несиловые передачи выполняют в основном кинематические функции и мощности практически не передают. Размеры таких передач определяются конструктивными соображениями.

Зубчатые передачи могут понижать или повышать частоту вращения ведомого вала. В понижающей передаче частота вращения ведомого вала (колеса) меньше, а в повышающей передаче больше частоты вращения ведущего вала (колеса).

Агрегат с понижающей передачей (передачами) называют редуктором, агрегат с повышающей передачей называют мультипликатором.

Точность изготовления и ее влияние на качество передачи.

Качество передачи связано с ошибками изготовления зубчатых колес и деталей (корпусов, подшипников и валов), определяющих их взаимное расположение. Деформация деталей под нагрузкой также влияет на качество передачи. Основными ошибками изготовления зубчатых колес являются: ошибка шага и формы профиля зубьев, ошибки в направлении зубьев относительно образующей делительного цилиндра.

Ошибки шага и профиля нарушают кинематическую точность и плавность работы передачи. В передаче сохраняется постоянным только среднее значение передаточного отношения . Мгновенные значения в процессе вращения периодически изменяются. Колебания передаточного отношения особенно нежелательны в кинематических цепях, выполняющих следящие, делительные и измерительные функции (станки, приборы и др.). В силовых быстроходных передачах с ошибками шага и профиля связаны дополнительные динамические нагрузки, удары, вибрации и шум в зацеплении.

Ошибки в направлении зубьев в сочетании с перекосом валов вызывают неравномерное распределение нагрузки по длине зуба.

Точность изготовления зубчатых передач регламентируется

ГОСТ1643–81, который предусматривает 12 степеней точности. Каждая степень точности характеризуется тремя показателями:

1) нормой кинематической точности, регламентирующей наибольшую погрешность передаточного отношения или полную погрешность угла поворота зубчатого колеса в пределах одного оборота (в зацеплении с эталонным колесом);

2) нормой плавности работы, регламентирующей многократно повторяющиеся циклические ошибки передаточного отношения или угла поворота в пределах одного оборота;

3) нормой контакта зубьев, регламентирующей ошибки изготовления зубьев и сборки передачи, влияющие на размеры пятна контакта в зацеплении (распределение нагрузки по длине зубьев).

Степень точности выбирают в зависимости от назначения и условий работы передачи. Наибольшее распространение имеют 6, 7 и 8-я степени точности (табл. 1). Стандарт допускает комбинацию степеней точности по отдельным нормам. Например, для тихоходных высоконагруженных передач можно принять

Таблица 1

Степень точности, не ниже	Окружная скорость м/с не более		Примечание
Степень точности, не ниже	Прямозубая	Косозубая	Примечание
6 (высокоточные)	15	30	Высокоскоростные передачи, механизмы точной кинематической связи — делительные, отсчетные и т.п.
7 (точные)	10	15	Передачи при повышенных скоростях и умеренных нагрузках или при повышенных нагрузках и умеренных ско ростях
8 (средней точности)	6	10	Передачи общего машиностроения не требующие особой точности
9 (пониженной точности)	2	4	Тихоходные передачи с пониженными требованиями к точности

повышенную норму контакта зубьев по сравнению с другими нормами, а для быстроходных малонагруженных — повышенную норму плавности и т. п.

Во избежание заклинивания зубьев в зацеплении должен быть боковой зазор. Размер зазора регламентируется видом сопряжения зубчатых колес.

Стандартом предусмотрено шесть видов сопряжения: H — нулевой зазор; E — малый зазор; С и D — уменьшенный зазор; В — нормальный зазор; А — увеличенный зазор.

При сопряжениях H, E и С требуется повышенная точность изготовления. Их применяют для реверсируемых передач при высоких требованиях к кинематической точности, а также при наличии крутильных колебаний валов,

Стандарт устанавливает также допуски на межосевые расстояния, перекос валов и некоторые другие параметры.

Пример условного обозначения точности цилиндрической передачи со степенью кинематической точности 8, по нормам плавности со степенью 7, по нормам контакта зубьев со степенью 6, с видом сопряжения В, видом допуска на боковой зазор – а и соответствием между видом сопряжения и классом отклонения межосевого расстояния. 8 – 7 – 6 – Ва ГОСТ1643–81.

Основные достоинства зубчатых передач

1. Постоянство передаточного числа.

2. Высокая нагрузочная способность, передаваемые моменты достигают5·10⁶ Нм.

3. Высокий К.П.Д. ( до 0,97…0,99 для одной пары колес ).

4. Малые габаритные размеры по сравнению с другими видами передач при равных условиях нагружения.

5. Большая долговечность и надежность в работе, простота обслуживания.

6. Сравнительно малые нагрузки на валы и опоры.

Недостатки зубчатых передач

Невозможность бесступенчатого изменения передаточного числа.
Высокие требования к точности изготовления и монтажа.
Шум при больших скоростях.
Плохие амортизационные свойства.
Потребность в специальном оборудовании и инструменте для нарезания зубьев.
Зубчатая передача не предохраняет машину от возможных опасных перегрузок.

Выбор материалов и расчет допускаемых напряжений

для зубчатых передач

Гузенков П.Г. «Детали машин», § 12.5.

Иванов М.Н. «Детали машин», § 8.13.

1. Исходные данные

1.1. Сведения о режиме нагружения:

T_п

t_h

Т_Н– номинальный крутящий момент;

t_h - время работы привода в часах;

T_i – нагрузка блока нагружения;

t_i – время действия блока нагружения в часах ;

, , ; где - - нагрузка блока в относительных единицах;

, , ; где - - время действия блока нагрузок в относительных единицах;

Tп = (1,3 …1,5 ) Tн - пусковой момент электродвигателя ( время действия в статических расчетах не учитывается).

Кгод – использование привода в течении года;

Ксут – использование привода в течении суток;

С (t) – срок службы, лет.

n – частота вращения ведущего вала передачи, об/мин.

1.2. Выбор материалов

Проектируемый привод относится к индивидуальному и мелкосерийному производству, содержащему мало – и средненагруженные передачи.

В случае использования упрощенной технологии изготовления зубчатых колес без последующего шлифования, применяют стали первой группы твердостью

Н < 350НВ, получаемую нормализацией или улучшением. Такие передачи в процессе работы прирабатываются, что ведет к снижению нагрузок в зацеплении зубьев. Для компенсации повышенного по сравнению с колесом числа циклов нагружения шестерни, ее твердость - Н₁ назначают больше твердости колеса Н₂ из условия :

Н₁ = Н₂ + ( 20 … 50 )НВ

Для передач редуктора выполненных из закаленных сталей с Н > 350НВ, требующих после термообработки шлифования, твердость шестерни и колеса назначают одинаковыми.

2. Расчет коэффициента долговечности

K _iL – коэффициент долговечности.

K_i_L = ,

m = 6 – при расчете по контактным напряжениям.

При расчете на изгиб:

m = 6 – термообработка нормализация или улучшение;

m = 9 – закалка.

i – индекс напряжений H или F.

2.1. Базовое число циклов нагружения – N_0.

Базовое число циклов перемены напряжений определяется по формуле :

при расчете по контактным напряжениям

N_НО = 30×НВ ^2,4 или N_НО = ( 1 … 12 )× 10⁷.

Рекомендуется принимать при термообработке:

нормализации или улучшении N_НО = 10⁷ циклов, закалке N_НО = 9× 10⁷ циклов.

при расчете по напряжениям изгиба N_F_О= (2...5 )×10 ⁶

Принимают N_F_О= 4×10 ⁶

2.2. Эквивалентное число циклов перемены напряжений

N _iE = 60× n_i × t_h × ,

где T_i – величина i -того момента гистограммы (см. график загрузки);

Т_H – величина расчетного (номинального) момента;

n_i– частота вращения вала, по которому ведется расчет передачи, об/мин;

t_i – продолжительность действия нагрузки T_i , в часах ;

t_h - общее время работы привода, рассчитывается следующим образом:

С – срок службы, лет;

t_h = С× k_c_ут× k_год× 365_дней× 24_часа;

Показатель степени – mc:

Расчет по контактным напряжениям – [ s_HP]: mc =3.

Расчет по напряжениям изгиба – [ s_FP]:

при нормализации или улучшении mc = 6;

при закалке mc = 9.

2.3. Коэффициент долговечности – K_iL

Расчет по контактным напряжениям – [ s_HP]:

Для нормализованных и улучшенных колес 1 £ К_HL £ 2,6 .

Для закаленных колес 1 £ К_HL £ 1,8 .

Расчет по напряжениям изгиба – [ s_FP]:

Для нормализованных и улучшенных колес 1 £ К_F_L £ 2,08 .

Для закаленных колес 1 £ К_FL £ 1,6 .

Если расчетное значение коэффициента К_iL выходит за указанный интервал, то принимают его крайние значения.

3. Расчет допускаемых напряжений

3.1. Допускаемые контактные напряжения при расчетах на выносливость определяются отдельно для зубьев шестерни и колеса с учетом термообработки и числа циклов нагружения:

[ s_HP] = × Z_R×Z_V,

где S_H – коэффициент безопасности ,

при НВ < 350 S_H=1,1;

при НВ > 350 S_H =1,2.

Z_R– коэффициент, учитывающий шероховатость рабочих поверхностей зубьев,

при R_a =1,25...0,63 Z_R=1 ;

Z_V=1...1,16 – коэффициент, учитывающий влияние окружной скорости;

При V< 5 м/с Z_V = 1

s_hlim= _limb_×K_HL– предел контактной выносливости, соответствующий эквивалентному числу циклов перемен напряжений (МПа);

где _lim_b – предел контактной выносливости, соответствующий базовому числу циклов перемен напряжений.

При НВ < 350 (нормализация или улучшение)

_lim_b= 2HB + 70

При закаленных сталях с НВ > 350

Поверхностная закалка _lim_b= 17·HRC + 200

Объемная закалка _lim_b= 17·HRC + 100

При расчете прямозубых колес [ s_HP] выбирают по слабому звену.

При расчете косозубых колес отличающихся по твердости на 60 …100 НВ

и V < 20 м /с допускаемое напряжение рассчитывают следующим образом

[ s_HP] = 0,5( [ s_HP₁] + [ s_HP₂]), или

[ s_HP] = 0,5( [ s_HP₁] + [ s_HP₂]), но £ 1,24 [ s_HP]_min – для цилиндрических колес.

[ s_HP] = 0,5( [ s_HP₁] + [ s_HP₂]), но £ 1,15 [ s_HP]_min – для конических колес.

3.2. Допускаемые напряжения при расчетах на выносливость по напряжениям изгиба определяется отдельно для зубьев шестерни и колеса, с учетом условий работы.

_FP]_i = × Y_R×Y_S,