Системы линейных уравнений

Пусть дана система линейных уравнений относительно неизвестных 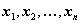. Уравнения системы будем считать пронумерованными — первое, второе и т. д. Коэффициенты при неизвестных в 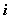-м уравнении системы обозначим через 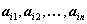(первый индекс - номер уравнения, второй - номер неизвестного, при котором стоит этот коэффициент), а свободный член 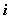-го уравнения — через 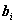. Тогда система линейных уравнений будет выглядеть следующим образом:

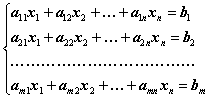Заметим, что в системе уравнений количество неизвестных может не совпадать с числом уравнений.

Систему линейных уравнений можно представить также в виде таблицы

в 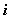-й строке которой, 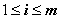записаны коэффициенты при неизвестных и свободный член 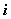-го уравнения системы.

Решением системы уравнений называется такая последовательность чисел 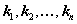, которая является решением каждого уравнения системы. Решить систему уравнений — значит найти все ее решения или убедиться в том, что их нет.

Возможны только следующие три случая:

1) система уравнений несовместна, т. е. не имеет ни одного решения;

2) система уравнений является определенной, т. е. имеет единственное решение;

3) система уравнений является неопределенной, т. е. имеет бесчисленное множество решений.

Система уравнений, которая имеет хотя бы одно решение, называется совместной.

Пусть система уравнений содержит противоречивое уравнение. Так как противоречивое уравнение не имеет решений, то система, содержащая противоречивое уравнение, несовместна.

Чтобы найти все решения системы уравнений или установить их отсутствие, следует преобразовать данную систему уравнений к такому виду, из которого можно сделать однозначное заключение о ее разрешимости.

Неизвестное 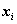называется разрешенным, если какое-нибудь уравнение системы содержит неизвестное 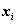, с коэффициентом, равным единице, а во все остальные уравнения системы неизвестное 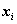не входит, т. е. входит с коэффициентом, равным нулю.

Пример. Система уравнений

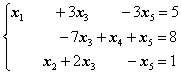
содержит разрешенные неизвестные 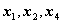. Неизвестные же 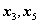не являются разрешенными.

Если каждое уравнение системы содержит разрешенное неизвестное, то такую систему называют разрешенной.

Из каждого уравнения разрешенной системы выберем по одному разрешенному неизвестному. Тогда получим набор неизвестных, которые называется набором разрешенных неизвестных данной разрешенной системы, который в общем случае определен неоднозначно.

Неизвестные системы линейных уравнений, которые не входят в данный набор разрешенных неизвестных, называются свободными неизвестными.

В приведенном примере свободными неизвестными являются .

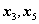Пусть дана система линейных уравнений. Требуется найти все решения этой системы. Ясно, что при решении этой задачи исходную систему уравнений можно заменить равносильной ей системой. Доказано, что любая совместная система линейных уравнений равносильна разрешенной системе линейных уравнений, полученной из исходной системы при помощи элементарных преобразований, под которыми понимается любое из следующих действий:

1) вычеркивание уравнения системы, у которого все коэффициенты при неизвестных и свободный член равны нулю, т. е. вычеркивание тривиального уравнения;

2) умножение обеих частей какого-либо уравнения системы на отличное от нуля число;

З) замена 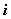-го уравнения системы уравнением, которое получается путем почленного сложения 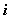-го и 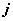-го уравнений системы.