Системы линейных уравнений с квадратной матрицей

Рассмотрим систему линейных уравнений с квадратной матрицей системы :

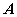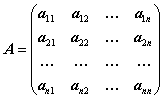
и двумя матрицами-столбцами 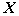(неизвестные) и 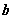(свободные члены):

, .

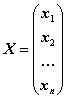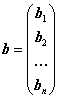Очевидно, систему линейных уравнений можно записать в матричном виде:

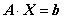
В данной системе число уравнений равно числу неизвестных.

Теорема. Если в системе уравнений определитель квадратной матрицы 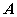не равен нулю, то система уравнений имеет единственное решение (см. критерий Кронекера-Капелли).

В данном случае матрица 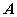называется невырожденной.

Кроме предыдущих методов решения существуют два способа решения систем с квадратной матрицей: формулы Крамера и матричный метод.

Формулы Крамера

Назовем столбцы матрицы 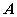следующим образом: первый столбец - ,

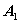второй столбец - 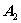, и т.д.,

последний столбец - .

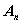Тогда 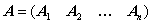. Составим 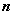дополнительных матриц:

, , …, ,

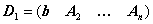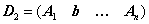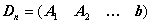и вычислим их определители и определитель исходной матрицы:

, , , …, .

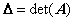Значения неизвестных вычисляются по формулам Крамера:

, , …, .

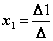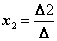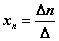Пример. Решить систему уравнений методом Крамера.

, .

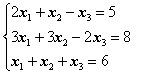
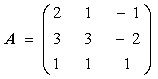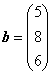Тогда , , .

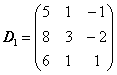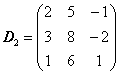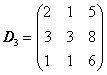Вычисляя определители этих матриц, получаем , , , .

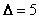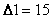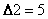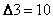И по формулам Крамера находим: , , .
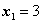
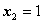
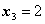