Решение системы с помощью обратной матрицы

Теорема. Если матрица 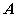обратимая матрица, то обратная к ней матрица 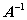вычисляется по следующему правилу:

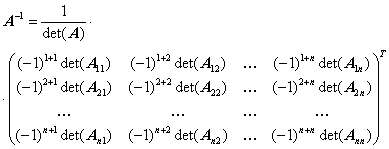Таким образом, обратная матрица – это транспонированная матрица алгебраических дополнений, умноженная на коэффициент .

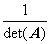Следует отметить, что обратная матрица существует, тогда и только тогда, когда определитель исходной матрицы отличен от нуля.

Теперь, рассмотрим матричное уравнение 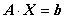. Если у матрицы 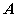существует обратная матрица 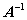, то умножая матричное уравнение на 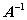слева, получим:

.

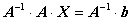По определению обратимости матрицы 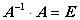и по свойству единичной 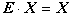, получаем:

.

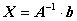Пример. Решить систему уравнений с помощью обратной матрицы.

, .

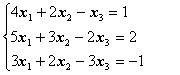
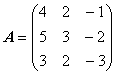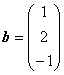Вычислим определитель матрицы 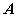, разлагая по первой строке:

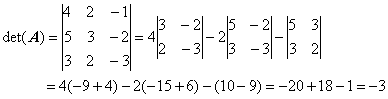
Значит, обратная матрица существует.

Вычислим алгебраические дополнения элементов матрицы:

,

,

,

,

,

,

,

,

.

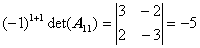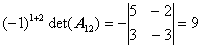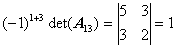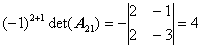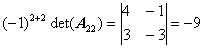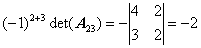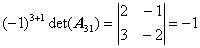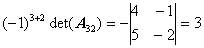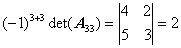Тогда решение системы получается умножением обратной матрицы на столбец свободных членов
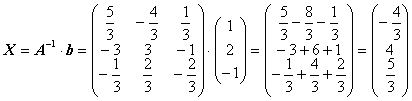