![]()
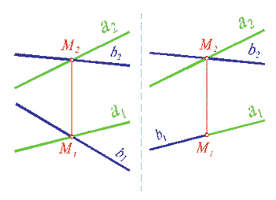
При изучении раздела "Задание геометрических образов на чертеже" мы рассматривали позиционные задачи и о принадлежности им точки. Однако точка может принадлежать одновременно двум геометрическим образам. Так, если точка принадлежит двум прямым, то об этом событии принято говорить: "Прямые пересекаются в данной точке" (рис. 80, 81).
|
Рис. 80
|
Рис. 81
|
В точке могут пересекаться любые линии - прямые и кривые, линии и поверхности, две поверхности при их точечном касании. Например, общая точка сферы и касательной к ней плоскости.
В общем случае поверхности и плоскости пересекаются по линиям. Эти линии могут быть прямыми, если пересекаются линейчатые поверхности, и кривыми, и ломаными при пересечении гранных и криволинейных поверхностей. Кривые и ломаные линии пересечения могут быть пространственными и плоскими. Плоские линии пересечения поверхности условились называть сечением.
Методика решения позиционных задач на пересечение геометрических образов основана на 3-х алгоритмах. Выбор алгоритма решения зависит от структуры геометрических образов и их ориентации относительно плоскостей проекций. Задача существенно упрощается, если оба геометрических образа или хотя бы один из них являются проецирующими. Такое положение принято называть решающим, что объясняется следующими рассуждениями.
Известно, что одна из проекций проецирующего геометрического образа обладает собирательным свойством (см. рис. 7). Следовательно, вырожденной проекции принадлежит и проекция точки или линии пересечения геометрического образа с другим. Условимся обозначать проецирующий геометрический образ символом _|_|_ , а не проецирующий - _\_/_ .
Запишем возможные варианты сочетаний:
1. _|_|_ З _|_|_
2. _|_|_ З _\_/_
3. _\_/_ З _\_/_