• Общие сведения
• Сферы - посредники

Общие сведения

На рис. 287 мы уже проследили построение линии пересечения двух поверхностей вращения, оси которых параллельны. В качестве посредников были применены параллельные секущие плоскости.

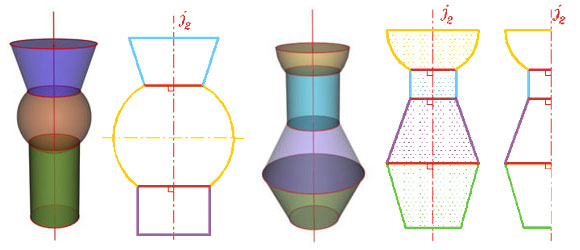
Если же оси вращения совпадают, то такие поверхности вращения называются соосными, или коаксиальными. Они пересекаются по общим параллелям (рис. 288 - 292).

Рис. 288

Рис. 289

Рис. 290

Рис. 291

Рис. 292

Число общих параллелей - линий пересечения - равно числу точек пересечения их полумеридианов (рис. 288). Заметим, что вырожденные проекции параллелей всегда перпендикулярны невырожденной проекции оси вращения.

Пересечение поверхностей вращения может происходить по одной параллели, образующей или точке. В таком случае касание может быть как внутренним, так и внешним.

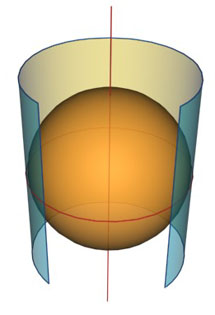Рис. 293

Рис. 294

Так, сфера может касаться поверхности цилиндра по их общей параллели, которая проходит на одном уровне с центром сферы, то есть по её экватору (рис. 293, 294).

Рис. 295

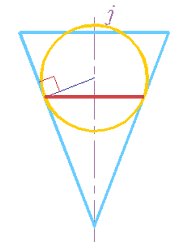Рис. 296

Чтобы определить уровень параллели касания поверхности сферы с поверхностью конуса, следует на проекции, где ось вращения проецируется в натуральную величину, провести из проекции центра сферы прямую, перпендикулярную образующей конуса до их пересечения (рис. 295, 296). Из точки пересечения строят вырожденную в отрезок проекцию общей параллели, перпендикулярную проекции оси вращения.

Сферы-посредники

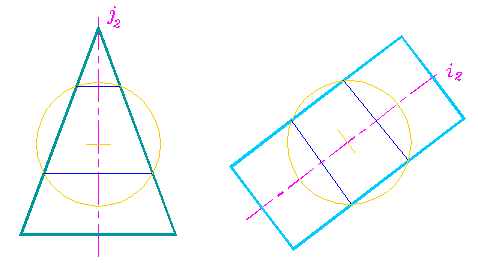
Пересечение любой поверхности вращения со сферой, центр которой лежит на оси вращения, всегда происходит по одной или двум параллелям - окружностям (рис. 297а, б). Так как ось вращения сферы может иметь любое направление, то в описанной ситуации сфера оказывается соосной с любой поверхностью вращения. Поэтому сферу удобно использовать в качестве посредника.

В качестве посредника сферу используют в том случае, если оси поверхностей вращения пересекаются. При этом для решения задачи необходимо, чтобы плоскость, образованная пересекающимися осями, была параллельна одной из плоскостей проекций.

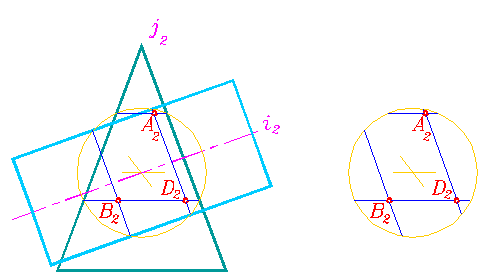
Если центр посредников (концентрических сфер) поместить в точке пересечении осей заданных поверхностей вращения, то эти поверхности пересекутся со сферой-посредником по параллелям-окружностям (рис. 298). Вырожденные в отрезок проекции этих точек окружностей, расположенных на одной сфере, пересекаются в точке (точках) (рис. 299).

Эти точки двойные и расположены на линии пересечения симметрично относительно плоскости, которая образована пересекающимися осями. Проекции этих точек на другой плоскости проекций строятся на натуральных изображениях параллелей. Изменяя радиус сфер, можно получить ряд промежуточных точек линии пересечения.

Составим универсальный алгоритм решения задачи на построение линии пересечения поверхностей вращения с использованием в качестве посредников семейство концентрических сфер на примере рис. 300:

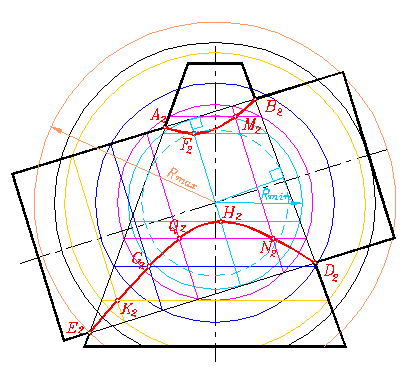
Рис. 300

1. Устанавливаем факт пересечения осей заданных поверхностей вращения.
2. При необходимости производим преобразование чертежа для того, чтобы плоскость, образованная пересечением двух осей вращения, заняла положение плоскости уровня.
3. Определяем проекции опорных точек в местах пересечения главных меридианов. В данном случае это точки А, B, D, E.
4. Определяем положение центра семейства концентрических сфер посредников в точке пересечения осей вращения заданных поверхностей.
5. Определяем минимальный радиус сферы-посредника. Минимальная сфера должна коснуться одной из поверхностей - пересечь ее по одной окружности (рис. 292 - 295), и в то же время пересечь вторую, потому что, если сфера не входит в контакт с одной из заданных поверхностей, она не может выполнять функцию посредника. С помощью минимальной сферы определяем точки, общие для данных поверхностей.
6. Радиус максимальной сферы посредника равен расстоянию от центра семейства сфер до наиболее удаленной опорной точки. В данном случае до точки Е.
7. Строим промежуточные точки линии пересечения с помощью сфер, радиус которых меньше максимального, но больше минимального. Сначала строим вырожденные в отрезки проекции линий-паралелей пересечения заданных поверхностей со сферой. Затем находим общие для паралелей точки. Рекомендуется незначительно изменять радиус следующей сферы-посредника.
8. Получив ряд дискретных точек объединяем их последовательно с опорными точками гладкой кривой.
9. Для построения второй проекции используем в качестве носителей точек уже построенные параллели на заданных поверхностях. В данном случае это горизонтальные параллели конуса, построенные при определении фронтальных проекций точек пересечения, ведь они на горизонтальную плоскость проекций проецируются без искажения.

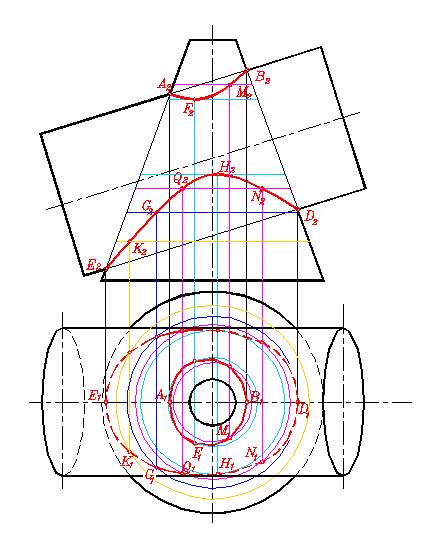
Рис. 300а

Для закрепления изучаемого материала решите задачу №56(4)

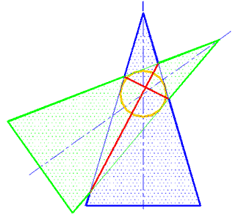Рис. 302

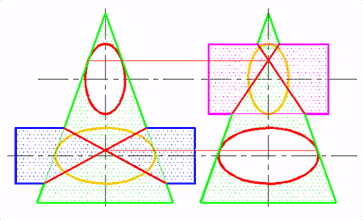Рис. 303

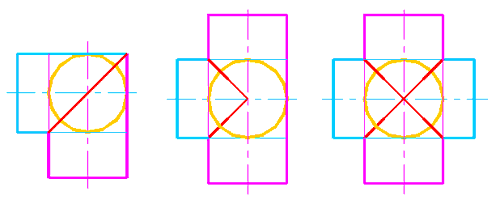
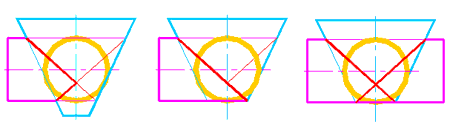
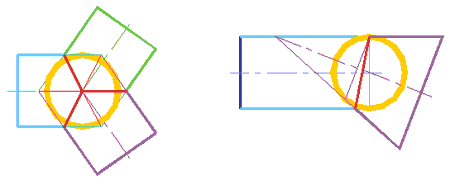
Если при определении радиуса минимальной сферы выяснится, что минимальная сфера касается сразу обеих поверхностей вращения, то линия их пересечении распадается на две плоские кривые второго порядка (рис. 301-313), что широко используется в технике при проектировании конструкций.

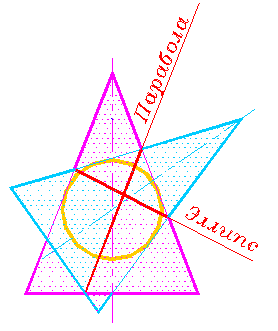Рис. 304

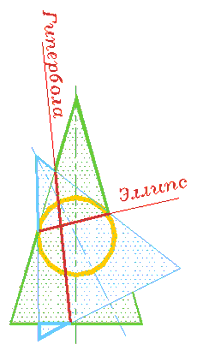Рис. 305

Рис. 306

Рис. 307

Рис. 308

Рис. 309

Рис. 310

Рис. 311

Рис. 312

Рис. 313

Гаспар Монж доказал теорему: если две кривые поверхности второго порядка пересекаются по одной кривой второго порядка, то они пересекаются по еще одной кривой - кривой второго порядка (рис. 314-317). Эта теорема позволяет разрабатывать более технологичные конструкции.

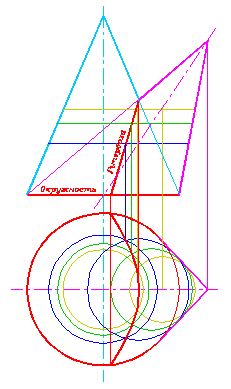Рис. 314

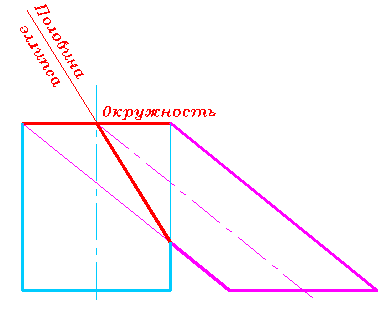Рис. 315

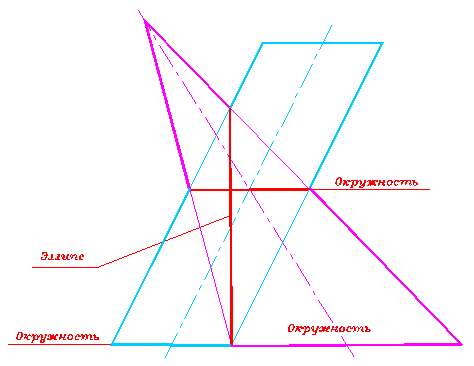
Рис. 316

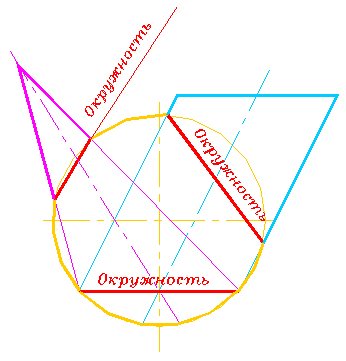
Рис. 317

Вопросы для самопроверки:
1. Что называется сечением?
2. Что называется позиционными задачами?
3. Назовите 3 типа решения главных позиционных задач по оределению общих элементов.
4. В каком случае общий элемент уже есть на двух проекциях и его надо только опознать?
5. Если общий элемент есть на одной из проекций, то из чего следует исходить при определении недостающей его проекции?
6. Для чего применяют посредники?
7. В каком случае в качестве посредников применяют плоскости?
8. Какие вы знаете простейшие линии на поверхности?
9. Что такое опорная точка?
10. Что применяют в качестве посредников при решении задач на пересечение поверхностей вращения у которых оси вращения лежат в одной плоскости?
11. Как определить уровень общей параллели касания сферы, которая находится внутри конуса?
12. Сколько надо применить посредников для определения линий пересечения двух плоскостей общего положения?
13. Нужны ли посредники при определении линии пересечения плоскости общего положения с плоскостью частного положения?
14. С какой плоскостью плоскость общего положения пересекается по фронтали?
15. По какой линии пересекаются две фронтально-проецирующие плоскости?
16. В каком случае плоскости пересекаются по горизонтально-проецирующей прямой?
17. Когда цилиндры пересекаются по прямым?
18. Что нужно, чтобы конусы пресекались по прямым линиям?
19. Назовите конические сечения. Сколько их?
20. Что является сечением плоскости?

[Содержание] [Первая] [Назад] [Вперед]