Второе сочетание - это пересечение проецирующего ГО с непроецирующим ( _|_|_ З _\_/_ ). Чтобы составить алгоритм решения таких задач рассмотрим два примера.
|
|
Пример 1. Плоскость общего положения, заданная двумя параллельными прямыми, пересекается горизонтально-проецирующей прямой t (рис. 267). Проекция прямой расположена вне проекций задающих плоскость параллельных прямых. Однако, мы знаем, что любая плоскость в пространстве бесконечна. Поэтому мы приходим к выводу о существовании точки пересечения заданной прямой и плоскости. Горизонтальная проекция этой точки, - назовем ее М, должна совпадать с вырожденной в точку проекцией прямой t - t1, так как точка М принадлежит этой проекции. В то же время точка М принадлежит плоскости. Поэтому вторую проекцию точки определяем из условия ее принадлежности заданной плоскости по уже отработанному алгоритму (рис 132): в плоскости вводим носитель для точки - прямую l М, которая проходит через точки А и 1 плоскости, и точку М, строим фронтальную проекцию носителя по точкам A и 1 и на ней определяем фронтальную проекцию искомой точки М. |
Пример 2. Определим проекции линии пересечения фронтально-проецирующей плоскости Y с поверхностью конуса вращения.
Фронтальная проекция линии пересечения (рис. 268, 269) определяется как часть следа проекции плоскости Y. Эта часть расположена между очерковыми образующими конуса. Данный конус - линейчатая поверхность вращения. Поэтому другую проекцию линии пересечения можно построить также из условия принадлежности дискретного - прерывистого, ряда точек, расположенных на поверхности конуса, и которые в тоже время составляют искомую линию. Сначала строим проекции опорных точек: двух точек, лежащих на линии обреза и точки, принадлежащей правой очерковой образующей фронтальной проекции конуса. При выполнении построений дискретного ряда точек в качестве их носителей на линейчатой поверхности вращения используют либо прямолинейные образующие (рис. 268), либо параллели (рис. 269).
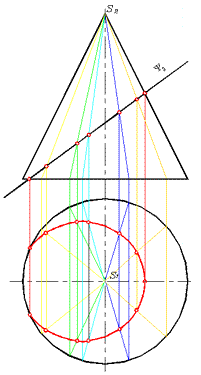 Рис. 268 |
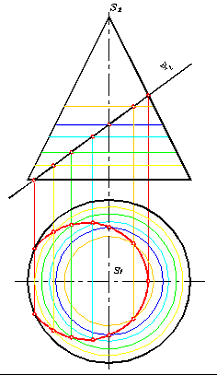 Рис. 269 |
Таким образом, алгоритм решения задач сочетания _|_|_ З _\_/_ , сводится к следующему:
Для закрепления изучаемого материала решите задачи: №27(3), №27(4), №28(5), №28(6), №57(2), №58
Сечением называется линия пересечения поверхности плоскостью.
Прежде чем приступить к разработке алгоритма решения задачи третьего сочетания _\_/_ З _\_/_ , рассмотрим сечения некоторых поверхностей вращения.
Все поверхности вращения второго порядка можно рассечь по кривым второго порядка: окружности, эллипсу, параболе, гиперболе, а линейчатые поверхности вращения еще по одной или двум прямым.
Сечение сферы всегда окружность, либо точка - в случае касания сферы секущей плоскостью.
Сечения цилиндра вращения - окружность, эллипс, две прямые или одна прямая в случае касания секущей плоскости.
Особый практический интерес представляют сечения конуса вращения - коники. Их семь. Вид коника зависит от расположения секущей плоскости относительно элементов, которые задают конус, его вершины, оси, образующей (рис. 270).
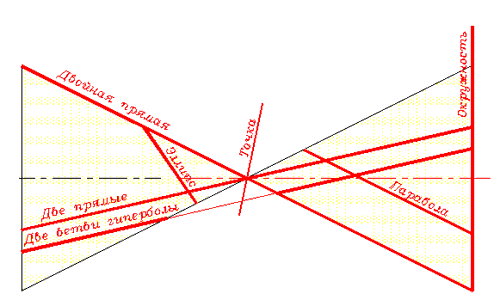
Рис. 270
ЭЛЛИПС - секущая плоскость пересекает все образующие и с осью вращения образует острый угол.
ОКРУЖНОСТЬ - секущая плоскость пересекает все образующие и перпендикулярна к оси вращения конуса.
ТОЧКА - секущая плоскость пересекает все образующие в месте их взаимного пересечения - в вершине.
ДВЕ ПРЯМЫЕ - секущая плоскость проходит через вершину и через две пересекающиеся в ней образующие.
СДВОЕННАЯ ПРЯМАЯ - секущая плоскость содержит в себе всего одну образующую. Такая секущая плоскость касается двух плоскостей конуса разными сторонами. Граница перехода сторон касания располагается в вершине. От нее как бы отходят две полупрямые.
ГИПЕРБОЛА - секущая плоскость параллельная двум образующим.
ПАРАБОЛА - секущая плоскость параллельная одной образующей.
Разницу между гиперболическим и параболическим сечениями легко определить, если руководствоваться правилом: если две полости конуса вращения пересекаются дважды секущей плоскостью, то в сечении получается две ветви гиперболы, а одна ветвь сечения двуполостного конуса является параболой.
|
Теперь проанализируем условие задачи, которая была представлена на рис. 268, 269. Секущая плоскость пересекает все образующие конуса, полное очертание которого прервано линией активного обреза конуса - окружностью основания. Кроме того, секущая плоскость с осью вращения конуса составляет острый угол. Следовательно, в данном случае сечение конуса представляет собой эллипс, точнее его часть больше половины. На рис. 271 повторено решение той же задачи с применением анализа условия: определены горизонтальные проекции параметров эллипса и по ним построена горизонтальная его проекция. АВ - большая ось эллипса, ED - малая ось эллипса. Горизонтальные проекции точек E и D построены с помощью прямолинейных образующих. По эллипсу, окружности, гиперболе, параболе можно рассечь и однополостный гиперболоид вращения. Его можно рассечь еще по двум параллельным прямым, которые представляют собой образующие двух семейств этой поверхности. Однако, в отличие от конических и цилиндрических поверхностей вращения, однополостный гиперболоид вращения нельзя пересечь плоскостью в одной точке и по одной прямой. |
Имея представление о возможных сечениях поверхностей вращения второго порядка, вы всегда сможете проанализировать верность результата проведенных построений.
Для закрепления изучаемого материала решите задачи: №47, №50, №51, №48, №56(3)