• Способ 1 (применение преобразования чертежа)
• Способ 2.1 (посредники - плоскости общего положения)
• Способ 2.2 (посредники - параллельные секущие плоскости)
• Опорные точки пересечения

Существуют различные способы решения этой задачи. Рассмотрим три из них.

Способ 1. (применение преобразования чертежа) Одну из плоскостей преобразуем в проецирующую и далее решаем задачу по алгоритму сочетания 2 - _|_|_ З _\_/_ (рис. 284).

Рис. 284

Для закрепления изучаемого материала решите задачу №54

Способ 2.1. Решение этим способом основано на решении задачи по определению точки пересечения прямой общего положения с плоскостью общего положения (см. рис. 274).

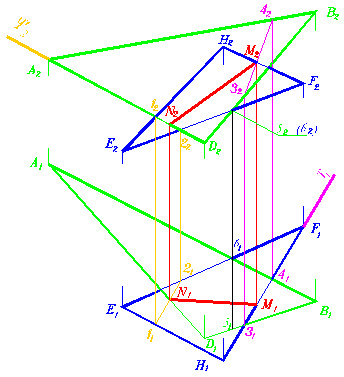
Рис. 285

Определим линию пересечения двух плоскостей, представленных треугольниками (рис. 285). Каждая плоскость представлена тремя прямыми. Совершенно естественно предположить, что эти прямые могут пересекаться с плоскостью другого треугольника. Но может случиться, что одна из сторон одного треугольника окажется параллельной плоскости другого треугольника. Но ведь в Вашем распоряжении шесть прямых и Вам представляется широкий выбор в построениях. Этот способ решения рекомендуется применять, если проекции плоскостей наложены.

Проследите за решением:

1. Предположим, что прямая AD пересекает плоскость треугольника EHF. Далее действуем по разработанному алгоритму.
   1. Вводим посредник-плоскость фронтально-проецирующую Y, которая содержит прямую AD. Об этом можно сказать: "Заключаем AD во фронтально-проецирующую плоскость-посредник".
   2. Посредник-плоскость Y , пересекает плоскость треугольника EHF по прямой 1-2. На чертеже Y₂ З D₂ (E₂H₂F₂) = (1₂ - 2₂).
   3. Горизонтальные проекции прямых AD и 1-2 пересекаются в точке N, которая является горизонтальной проекцией точки пересечения прямой AD с плоскостью EHF. N₂ принадлежит A₂D₂.

Переходим к определению второй общей точки.

2. Предположим, что прямая HF пересекается с плоскостью треугольника ABD. И опять действуем по разработанному алгоритму.
   1. Вводим посредник-плоскость, на этот раз горизонтально-проецирующую - Т (тау), которая проходит через прямую HF.
   2. Плоскость Т пересекает плоскость треугольника ABD по прямой 3-4.
   3. Фронтальные проекции HF и 3-4 определяют фронтальную проекцию точки М - точки пересечения HF с плоскостью треугольника ABD.

Заданные треугольники пересекаются по отрезку MN. Видимость частей треугольников устанавливается логически, а в спорной ситуации с помощью конкурирующих точек. Хотя при решении задачи путём преобразования чертежа видимость установить проще (рис. 284).

Для закрепления изучаемого материала решите задачу №29

Способ 2.2. (посредники - параллельные секущие плоскости). Если проекции плоских фигур не наложены, удобнее воспользоваться алгоритмом решения задач для сочетания 3, сущность которого представлена на рис. 273. Решим задачу по определению лини пересечения плоскостей..

Пусть даны две плоскости: Г (a || b) и D (d З m) (рис. 286). Требуется определить линию их пересечения.

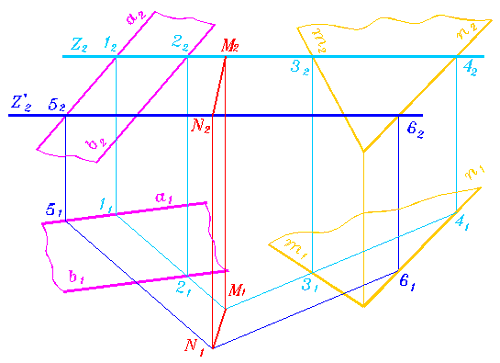
Рис. 286

Действуем по алгоритму:

1. Вводим посредник - горизонтальную плоскость уровня - Z (дзета).
2. Посредник-плоскость Z пересекает плоскость Г по горизонтали 1-2, а плоскость D - по горизонтали 3-4.
3. Горизонтали 1-2 и 3-4, располагаясь в одной плоскости, пересекаются в точке М, что определяется пересечением их горизонтальных проекций. Фронтальная проекция точки М располагается на высоте плоскости Z, принадлежит ее следу, а также фронтальным проекциям прямых 1-2 и 3-4.

Для определения второй точки линий пересечений заданных плоскостей рекомендуется воспользоваться второй горизонтальной плоскостью уровня, так как горизонтали, принадлежащие одной плоскости, между собой параллельны - вспомните ступени лестницы, которые являются горизонталями ее плоскости.

Продолжим построения:

1. Несколько ниже (чем ниже, тем точнее будут построения) вводим посредник - горизонтальную плоскость уровня Z'.
2. Она пересекает плоскости Г и D по их горизонталям, для построения горизонтальных проекций которых достаточно определить по одной точке пересечения с плоскостью-посредником, так как нам известны направления горизонталей этих плоскостей. На чертеже это точки 5 и 6.
3. Пересечение новых горизонталей определяет вторую общую для заданных плоскостей точку N.
4. Для построения искомой прямой нами определены две точки М и N. Попарно соединяем их одноименные проекции, завершая решение задачи.

Этим способом можно было решить задачу на пересечение плоскостей, представленных двумя наложенными проекциями треугольников, однако нам пришлось бы построить большее количество линий и точек.

Этот способ позволил нам ближе познакомиться с применением параллельных секущих плоскостей-посредников. Для определения прямой линии пересечения двух плоскостей нам понадобилось всего две плоскости-посредника.

Параллельные плоскости-посредники рекомендуется применять при построении линии пересечения поверхностей вращения, оси вращения которых перпендикулярны к одной и той же плоскости проекций. В этом случае на плоскости проекций сечения плоскостью-посредником параллели поверхностей вращения проецируются в натуральную величину (рис. 273). Решим этим же способом задачу по определению линии пересечения двух поверхностей вращения: отсеков "квадратного" тора и сферы (рис. 287).

Рис. 287

Прежде чем приступить к решению данной задачи, предопределим характер линии пересечения. Поскольку пересекаются две поверхности второго порядка, то линия их пересечения должна быть кривой четвертого порядка. Кривая четвертого порядка - линия двоякой кривизны, любая ее проекция кривая линия. Поэтому проекцию искомой линии будем строить по дискретному ряду ее точек, которые затем соединим плавной кривой.

Еще до применения посредников в данном случае необходимо определить опорные точки линии пересечения.

Для закрепления изучаемого материала решите задачу №56(2)

Опорные точки линии пересечения

Опорными точками линии пересечения называются точки, которые обладают геометрическими свойствами, существенно отличающими их от всех других точек линии пересечения.

К опорным точкам относят самые высокие и самые низкие точки; точки границ видимости - точки, которые отделяют видимую часть линии пересечения от невидимой; самые левые и самые правые точки; точки пересечения ребер многогранной поверхности с другой поверхностью, как точки 1, 2, 3 на рис. 275; точки, проекции которых являются особыми точками для линии пересечения - например, точки самопересечения кривой; точки, проекции которых являются главными для построения линии пересечения - например, вершины кривой второго порядка, как точки А, В, D, E на рис. 271, и так далее.

Проекции опорных точек строятся по определенным законам еще до введения посредников. На чертеже опорные точки рекомендуется обозначать буквами.

В данной задаче опорными точками являются точки А, В и В'. Точка А является самой высокой точкой линии пересечения. Её положение определяется пересечением фронтальных проекций очерковых линий заданных поверхностей, их главных меридианов. Главные меридианы заданных поверхностей располагаются в одной фронтальной плоскости уровня, которая является плоскостью симметрии данного сочетания фигур, и следовательно, плоскостью симметрии и для линии их пересечения. Точки В и В' получены при пересечении горизонтальных проекций экваторов заданных поверхностей. Заданные поверхности имеют общую горизонтальную плоскость экваторов, по которым они обрезаны. Эти точки являются самыми низкими у линии пересечения. Кроме того у линии пересечения точка В - самая близкая, а точка В' - самая далекая по отношению к наблюдателю. Эти точки являются самыми удалёнными от плоскости симметрии для искомой линии пересечения и равноудалёнными от плоскости симметрии.

Вы убедились, что для определения проекций опорных точек нам не пришлось выполнять никаких построений, кроме линий связи, устанавливающих недостающие проекции точек. Достаточно было лишь доказать их принадлежность линии пересечения.

Опорные точки служат как бы вехами для построения линии пересечения, но их недостаточно, чтобы полностью отразить саму кривую линию пересечения. Опорных точек бывает достаточно при построении линии пересечения плоскостей и многогранных поверхностей.

Дополним ряд опорных точек дискретным рядом промежуточных точек, которые мы определим с помощью параллельных плоскостей-посредников Z¹, Z², Z³, Z⁴. Каждая из указанных плоскостей-посредников пересекает заданные поверхности по их параллелям. Параллели располагаются попарно в каждой из плоскостей-посредников и взаимно пересекаются в точках, которые принадлежат обеим поверхностям, так как лежат на их линиях. Полученные промежуточные точки вместе с опорными составляют дискретный ряд точек линии пересечения. Соединяем их в логической последовательности плавной кривой линией. Очевидно, что применять посредники за пределами опорных точек не имеет смысла.

Употребление в качестве посредников параллельных плоскостей применимо не только для поверхностей вращения, а также для других поверхностей, которые посредники могут пересекать по простейшим линиям - прямым или окружностям.

[Содержание] [Первая] [Назад] [Вперед]