2. Пересечение проецирующих ГО

Для первого сочетания ( _|_|_ З _|_|_ ) возможны варианты: 1.1 - пересекающиеся геометрические образы являются проецирующими на разные плоскости проекций; 1.2 - оба геометрических образа являются проецирующими на одну и ту же плоскость проекций.

Общим правилом для этих двух вариантов первого сочетания _|_|_ З       _|_|_, является то, что на чертеже уже существуют проекции их общего элемента - точки или линии. Так, на рис. 252, 253 представлено пересечение горизонтально-проецирующей прямой t и фронтально-проецирующей прямой u. Они пересекаются в точке А. Проекции точки А совпадают с вырожденными в точки проекциями этих прямых: А₁ = t₁, A₂ = u₂.

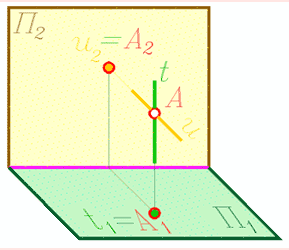Рис. 252

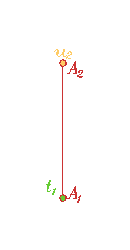Рис. 253

На рис. 254, 255 горизонтально-проецирующая прямая t пересекается с фронтально-проецирующей плоскостью Y в точке А. При этом А₁ совпадает с вырожденной в точку проекцией горизонтально-проецирующей прямой T, А₂ принадлежит следу плоскости Y - Y₂, и расположена на пересечении обычной проекции прямой t - t₂, c Y₂.

Для закрепления изучаемого материала решите задачи: №52, №28(1), №28(2), №28(3), №27(1), №27(2)

На рис. 256, 257 представлены две пересекающиеся фронтально-проецирующие плоскости Y и W. Очевидно, они пересекаются по фронтально-проецирующей прямой u.

Для закрепления изучаемого материала решите задачу №27(1)

Усложним задачу. Определим линию пересечения двух плоскостей общего положения, которые являются простейшими линейчатыми поверхностями (рис. 258, 259).

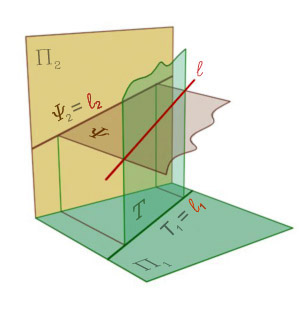Рис. 258

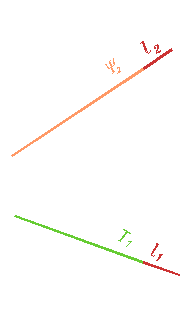Рис. 259

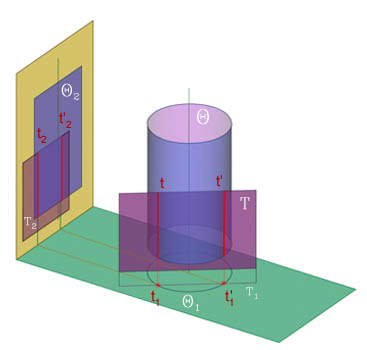
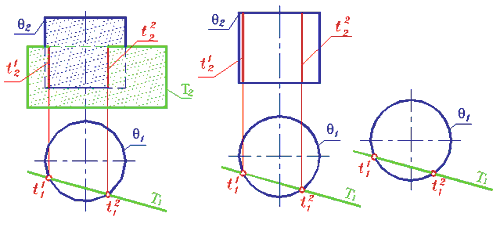
Фронтально-проецирующая плоскость Y пересекается с горизонтально-проецирующим цилиндром q (рис. 260) по замкнутой кривой е. Обратимся теперь к чертежу - рис. 261. След плоскости Y пересекает фронтальную невырожденную проекцию горизонтально-проецирующего цилиндра вращения q. Очевидно, что линия пересечения - эллипс. Фронтальная проекция эллипса является отрезком, который заключен между очерковыми образующими цилиндра, а горизонтальная совпадает с вырожденной в окружность проекцией цилиндра.

Для закрепления изучаемого материала решите задачи: №27(2) и №28(2)

Мы знаем, что две непараллельные плоскости пересекаются по прямой. Поэтому нам необходимо определить проекции линии пересечения горизонтально-проецирующей плоскости Т, и фронтально-проецирующей плоскости Y, которые по своей природе не могут быть параллельными. Следовательно, существует их линия пересечения. В то же время заданные плоскости представлены своими следами, которые содержат в себе проекции любой фигуры, принадлежащей им. Поэтому проекции линии пересечения совпадают со следами заданных плоскостей. В приведенном примере линией пересечения является прямая общего положения.

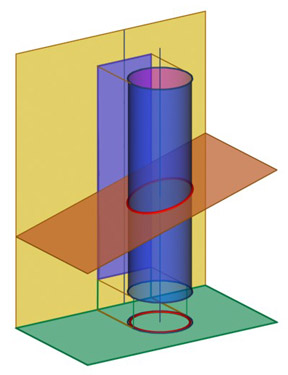Рис. 260

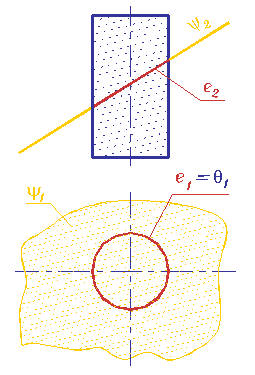Рис. 261

Для закрепления изучаемого материала решите задачи №56(1) и №56(3)

Рассмотрим пересечение двух криволинейных поверхностей - цилиндров вращения, каждый из которых является проецирующим: q _|_|_ П₁, W _|_|_ П₂. Рис. 265 показывает, что они пересекаются по пространственной кривой - линии двоякой кривизны , так как две поверхности второго порядка в общем случае пересекаются по кривой четвёртого порядка , которая в особых случаях распадаются на две кривые второго порядка, с узловой точкой. На чертеже Монжа (рис. 266) проекциями линии пересечения являются: на фронтальной - окружность, которая совпадает с вырожденной проекцией цилиндра W , а на горизонтальной - это часть окружности - вырожденной проекции цилиндра Q , которая ограничена очерком цилиндра W .

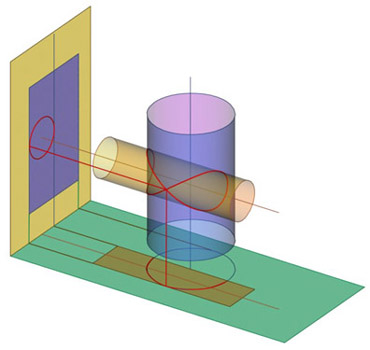Рис. 265

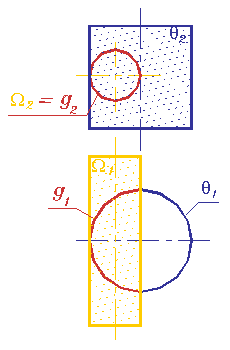Рис. 266

Рассмотрим вариант 1.2 сочетания _|_|_ З _|_|_

Совершенно естественно предположить, что оба геометрических образа могут оказаться проецирующими на одну и ту же плоскость проекций.

В этой ситуации пересечение происходит по одной (рис. 262, 263) или более проецирующих на ту же плоскость проекций прямых. Такие прямые могут быть представлены на чертеже одной проекцией - точкой (рис. 264). Таким образом два геометрических образа могут пересекаться по проецирующим прямым в том случае, если оба они являются проецирующими на одну и ту же плоскость проекций.

Рис. 262

Рис. 263

Рис. 264

Анализируя рассмотренные примеры можно сделать вывод о том, что на чертеже уже имеются проекции общего элемента и они принадлежат вырожденным проекциям пересекающихся геометрических образов. Поэтому алгоритм решения задач сочетания _|_|_ З _|_|_ . включает:

1. Мысленное представление общего элемента на чертеже и его обозначение.
2. Опознание проекций общего элемента на чертеже и его обозначение.

Для закрепления изучаемого материала решите задачи: №57(1), №57(3)

[Содержание] [Первая] [Назад] [Вперед]