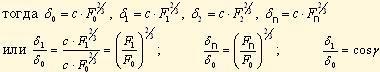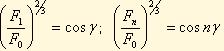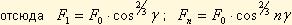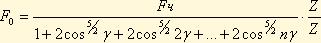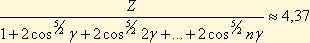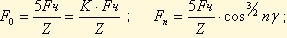Условия работы подшипников качения, влияние на его работоспособность.
При радиальном нагружении подшипника силы действующие на тела качения распределяются не равномерно. В восприятии нагрузки участвуют только тела качения, расположенный на дуге не превышающей 180? (нагруженная зона). Задача распределения сил между телами качения является статически неопределимой.
По условию равновесия внутреннего кольца
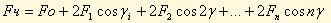 где
где
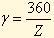
,а Z - число шариков; ηγ < 90°
Пренебрегая изгибом колец их деформацию можно представить
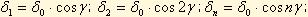 n - номер тела качения.
n - номер тела качения.
Согласно теории контактных деформаций зависимость между деформацией шарика σ и вызывающей деформацию силой Fч можно написать в следующей формуле
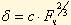 где с - коэффициент пропорциональности,
где с - коэффициент пропорциональности,
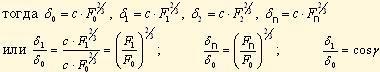
Согласно предыдущим равенствам можно написать, что
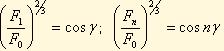
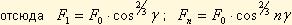
Подставляя полученный значения в исходную формулу и решая относительно Fo получим:
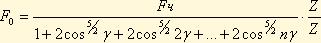
Подсчитанной, что отношение
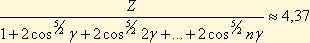
для любого числа шариков, встречающегося в подшипниках. При этом F0=4,37 Fч/Z.
Вводя поправку на влияние радиального зазора и неточности размеров деталей, практически принимают:
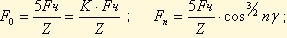
γ- угол наклона линии контакта.
Распределение нагрузки зависит от величины зазора в подшипниках и от точности геометрической формы его деталей. Зазоры увеличиваются от износа подшипника при эксплуатации. При этом прогрессивно ухудшается условие работы вплоть до разрушения подшипника.
<= [1] [2] [3] [4] [5] [6] [7] =>
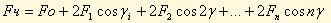 где
где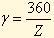
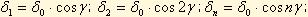 n - номер тела качения.
n - номер тела качения.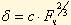 где с - коэффициент пропорциональности,
где с - коэффициент пропорциональности,