ЛАБОРАТОРНАЯ РАБОТА №3
Численное моделирование процессов пластической деформации
методом граничных элементов
Цель
работы: изучить методику
расчёта процесса пластической деформации с применением метода граничных
элементов и рассчитать перемещения граничных и внутренних точек,
рассматриваемого деформируемого тела.
Материалы,
инструмент, оборудование.
1. Условия
задач о растяжении плоского кольца внутренним усилием и осадке полосы.
2. Универсальная
программа TWO2D_PL.exe, реализованная на основе численного метода граничных
элементов (МГЭ).
3. ПК
и принтер.
Общие сведения.
L(U)+N(U)=P, (3.1)
где Р – некоторая известная функция.
Итерационный процесс основывается на представлении уравнения (3.1) в виде
L(U) =P – N(U )
(3.2)
Задаваясь начальным
значением U0 (в частности, U0 =0), получим:
L(U1) =P – N(U0 )
(3.2а)
Решение
повторяется до достижения требуемой точности величины U1.
Для
решения линейно-упругой задачи (L(U)), соответствующей рассматриваемой,
применяется гранично-элементное уравнение [6]
,
(3.3)
где pi – напряжения, а ui – перемещения на границе.
В настоящем решении используется известная аналогия между течением вязкой жидкости и упруго-деформируемым несжимаемым телом (коэффициент Пуассона равен 0.5). Благодаря такому подходу величины ui равны скоростям пластического течения в искомых точках на границе области. Для практического решения интегралы уравнения (3.3) заменяются суммами:
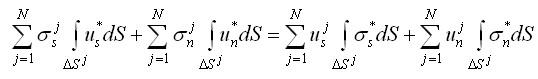 (3.4)
(3.4)
где N – число граничных элементов, DS j – их площадь.
Входящие
в уравнения (3.3) и (3.4) величины со звездочками полагаются известными,
например, определяющимися решением Кельвина. Для решения нелинейной задачи
пластической деформации (N(U)) используется итерационный цикл,
подчиняющийся зависимости:
k(an-1)an=fn-1. (3.5)
Один
из способов реализации метода упругих решений, расчёт на основе алгоритма
переменной вязкости и поправками к исходным данным. В этом случае соответствующие
зависимости имеют вид:
U(I)n+1= U(I)n+DU(I)n, (3.6)
где DU(I)n – величина поправки, учитывающая
изменение коэффициента жесткости при формоизменении.
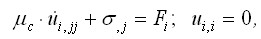 (3.7)
(3.7) где
компоненты массовой силы в каждой ячейке внутренней области определяются как
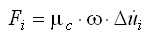 (3.8)
(3.8)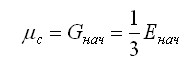 - начальное
значение коэффициента жесткости; G - модуль сдвига; - оператор Лапласа для
скорости перемещения; - параметр, характеризующий
уменьшение коэффициента жесткости в процессе деформирования.
- начальное
значение коэффициента жесткости; G - модуль сдвига; - оператор Лапласа для
скорости перемещения; - параметр, характеризующий
уменьшение коэффициента жесткости в процессе деформирования.В качестве
характеристики вязкости уже деформируемого металла использован известный в
теории обработки металлов давлением коэффициент жесткости
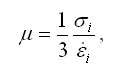 (3.9)
(3.9)где σi – интенсивность напряжений; σi – интенсивность скоростей
деформаций; E - текущее
значение модуля упругости
деформируемого металла.
Вследствие нелинейности зависимости 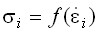 для деформируемых
материалов параметр уменьшения коэффициента жесткости в процессе деформирования
w на
итерациях будет равен
для деформируемых
материалов параметр уменьшения коэффициента жесткости в процессе деформирования
w на
итерациях будет равен
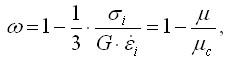 ,
(3.10)
,
(3.10)
а при рассмотрении новой стадии расчёта формоизменения первоначально ω=0, следовательно, Fi=0 согласно выражения (3.8).
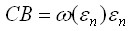 и в следующем приближении
полагается, что
и в следующем приближении
полагается, что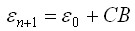 (3.11)
(3.11)
или
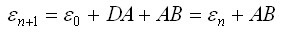 (3.11,а)
(3.11,а)
Как видно из рис.3.1, процесс последовательных приближений
(итерационный процесс) сходится к точному значению деформации εm, если функция ω(ε) непрерывна и удовлетворяет
условиям
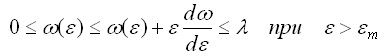 (3.12)
(3.12)
где λ<1 -
константа.
Однако
следует иметь в виду, что скорость сходимости существенно зависит от вида
функции ω(ε). Если материал обладает большим
упрочнением, т.е. кривая мало отклоняется от прямой σ=Ee или,
что то же самое, функция ω(ε) мала, то уже 3-4 приближения дают
достаточно точное значение деформации. И наоборот, если материал обладает малым
упрочнением, то может потребоваться значительное число итераций (приближений)
чтобы получить значение деформаций с требуемой точностью [7].
Следует
отметить, что рассмотренная методика является универсальной и пригодна для
расчёта поковок любой конфигурации.
Обобщённая
блок-схема алгоритма гранично-элементного расчёта нелинейной задачи
формоизменения приведена на рис.3.2.
Порядок выполнения
работы.
1. Изучить методику гранично-элементного
расчёта
2. На основе программного решения задач
о растяжении плоского кольца внутренним усилием и осадке полосы получить данные
о деформировании заданных тел под действием рассматриваемого нагружения.
3. Сделать выводы по работе о характере
формоизменения граничного контура и внутренних ячеек.
Условия
заданий.
ЗАДАНИЕ
1. В качестве первого тестового примера используем задачу о растяжении плоского
кольца внутренним усилием рис.3.3.
Размеры
кольца: r=20 мм и R=40 мм; материал – алюминиевый сплав Д16 при t=400оС;
граничные условия: нормальное напряжение на внутреннем контуре 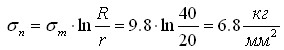 , касательное напряжение σs на поверхности контакта отсутствует;
на наружном контуре σn=σs=0.
, касательное напряжение σs на поверхности контакта отсутствует;
на наружном контуре σn=σs=0.
Ниже
приводится пример заполнения файла исходных данных для задачи о растяжении
плоского кольца с указанием принятых в нём форматов представления чисел (справа
по тексту). Более подробно порядок заполнения аналогичных файлов рассмотрен в
методической работе [10].
0.4999 3500.0000 0.0000 0.0000 (F6.4,3F12.4)
0.0000E 00 0.0000E 00 0.0000E 00 (3E11.4)
5 20.0000 0.0000 19.3185 5.1764 1 0.0000E 00-0.6800E 01 (I4,4F12.4,I4,2E11.4)
1 19.3185 5.1764 17.3205 10.0000 1 0.0000E 00-0.6800E 01
1 17.3205 10.0000 14.1421 14.1421 1 0.0000E 00-0.6800E 01
1 14.1421 14.1421 10.0000 17.3205 1 0.0000E 00-0.6800E 01
1 10.0000 17.3205 5.1764 19.3185 1 0.0000E 00-0.6800E 01
1 5.1764 19.3185 0.0000 20.0000 1 0.0000E 00-0.6800E 01
1 0.0000 40.0000 10.3528 38.6370 1 0.0000E 00 0.0000E 00
1 10.3528 38.6370 20.0000 34.6410 1 0.0000E 00 0.0000E 00
1 20.0000 34.6410 28.2843 28.2843 1 0.0000E 00 0.0000E 00
1 28.2843 28.2843 34.6410 20.0000 1 0.0000E 00 0.0000E 00
1 34.6410 20.0000 38.6370 10.3528 1 0.0000E 00 0.0000E 00
10 38.6370 10.3528 40.0000 0.0000 1 0.0000E 00 0.0000E 00
21.0000 1.0000 39.0000 1.0000 8 (4F12.4,I4)
22.0000 2.0000 22.0000 0.0000 1
24.0000 2.0000 24.0000 0.0000 1
26.0000 2.0000 26.0000 0.0000 1
28.0000 2.0000 28.0000 0.0000 1
30.0000 2.0000 30.0000 0.0000 1
32.0000 2.0000 32.0000 0.0000 1
34.0000 2.0000 34.0000 0.0000 1
36.0000 2.0000 36.0000 0.0000 1
38.0000 2.0000 38.0000 0.0000 1
1 11 2 13 12 4.0000 (5I4,F12.4)
2 14 3 16 15 4.0000
3 17 4 19 18 4.0000
4 20 5 22 21 4.0000
5 23 6 25 24 4.0000
6 26 7 28 27 4.0000
7 29 8 31 30 4.0000
8 32 9 34 33 4.0000
9 35 10 37 36 4.0000
ЗАДАНИЕ 2. В качестве второго тестового примера используем задачу о осадке полосы рис.3.4 из аналогичного материала, находящегося в аналогичном температурном режиме. Наружный контур описан 51 граничным элементом, а внутренняя область разбита на 20 ячеек, в которых вычислялись смещения и напряжения.
Трение
на контактной поверхности – максимальное (un=3.6, us=0); вторая граничная поверхность –
свободная (sn=ss=0).
2 12 4 20
0.4999 3500.0000 0.0000 0.0000
0.0000E 00 0.0000E 00 0.0000E 00
41 0.0000
10.0000 41.0000 10.0000 2
0.0000E 00-0.0018E 03
10 41.0000
10.0000 41.0000 0.0000
1 0.0000E 00 0.0000E 00
0.0000 6.0000 40.0000 6.0000 9
0.0000 2.0000 40.0000 2.0000 9
2.0000
8.0000 2.0000
0.0000 3
6.0000
8.0000 6.0000
0.0000 3
10.0000 8.0000 8.0000 0.0000 3
14.0000 8.0000 14.0000 0.0000 3
18.0000 8.0000 18.0000 0.0000 3
22.0000 8.0000 22.0000 0.0000 3
26.0000 8.0000 26.0000 0.0000 3
30.0000 8.0000 30.0000 0.0000 3
34.0000 8.0000 34.0000 0.0000 3
38.0000 8.0000 38.0000 0.0000 3
1 23 2 25 24 16.0000
2 28 3 30 29 16.0000
3 33 4 35 34 16.0000
4 38 5 40 39 16.0000
5 43 6 45 44 16.0000
6 48 7 50 49 16.0000
7 53 8 55 54 16.0000
8 58 9 60 59 16.0000
9 63 10 65 64 16.0000
10 68 11 70 69 16.0000
12 25 13 27 26 16.0000
13 30 14 32 31 16.0000
14 35 15 37 36 16.0000
15 40 16 42 41 16.0000
16 45 17 47 46 16.0000
17 50 18 52 51 16.0000
18 55 19 57 56 16.0000
19 60 20 62 61 16.0000
20 65 21 67 66 16.0000
21 70 22 72 71 16.0000
Результаты
решения заданий 1 и 2 хорошо согласуются с решениями, содержащимися в работах
[8] и [9], соответственно.
Содержание отчёта. Отчёт о выполнении работы должен
включать:
1. Название работы.
2. Цель работы.
3. Перечень материалов, инструментов и
оборудования.
4. Краткие теоретические сведения.
5. Условия задач, решаемых МГЭ.
6. Распечатки файла исходных данных и
файла результатов расчёта после достижения сходимости с точным решением.
7. Картины деформированного состояния
граничного контура и внутренних ячеек сечения изделия.
8. Выводы по работе.
Скачать архив