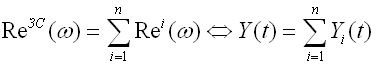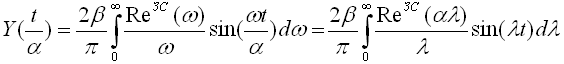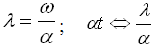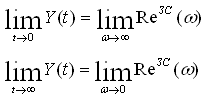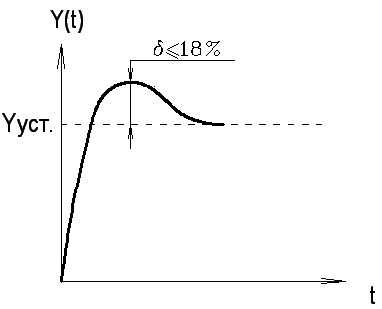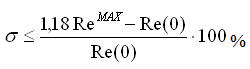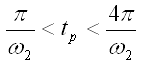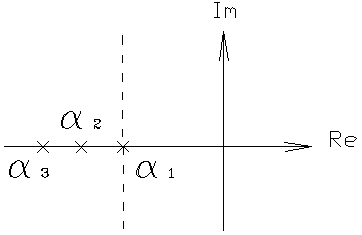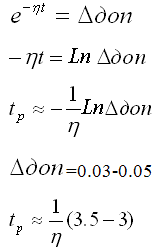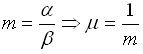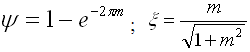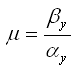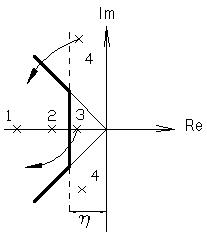| Лекции по ТАУ | Методические указания | Программные средства | Контрольные вопросы | Тестирование | Дополнительно |
5.1. Основные понятия и определения.
5.2. Испытательные воздействия для оценки качества управления. 5.3. Прямые методы исследования качества САУ. 5.4. Построение переходного процесса в САУ. 5.5. Оценка качества САУ по виду ПП. 5.6. Аналитические методы анализа частных показателей точности работы автоматических систем. 5.7. Частотные методы приближенной (косвенной) оценки качества линейных систем. 5.8. Качественная и приближенная количественная оценки переходных процессов в линейных системах по их ВЧХ. 5.9. Оценка колебательности ЗС по максимуму АЧХ. 5.10. Оценка быстродействия ЗС по частоте среза амплитудной характеристики РС. 5.11. Корневые методы оценки качества систем 5.1. Основные понятия и определения. Под качеством управления в динамической системе понимают совокупность показаний, как количественного, так и качественного характера, которые характеризуют основные свойства системы, и в установившемся состоянии и в процессе реализации функции управления (в статике и динамике). Эти показатели также должны позволять произвести оценку соответствия результатов управления целям и требованиям управляемой технологии. К качественным показателям относятся такие оценки характера управления, как быстродействие, колебательность или апериодичность системы, статизм, астатизм и т.д. Для оценки качества систем управления, используется такое понятие, как критерий качества (КК). Под ним понимают математическое выражение или их систему, позволяющую вычислить количественную оценку качества управления по результатам исследования системы или ее ММ. При такой оценке критерий качества может быть либо скалярным, либо векторным. 1) критерием качества (КК) является его быстродействие, выраженное временем затухания в системе ПП, вызванного определенным видом воздействия (как по месту приложения, так и по форме); 2) критерием качества является максимальное значение модуля ошибки, регулируемого в процессе ее устранения; 3) критерием качества является энергия осуществления управления. Векторный КК характеризуется некоторым множеством показаний (обычно упорядоченным) называемым кортежем. Например, качество управления оценивается временем регулирования, максимальной ошибкой регулирования и энергией управления. Анализ и оценка качества управления систем с использованием векторных КК черезвычайно трудны. В связи с этим даже при необходимости векторной оценки качества системы стремятся тем или иным способом векторную оценку качества свести к скалярной. 5.2. Испытательные воздействия для оценки качества управления. В ТАУ нашли применение два подхода к оценке качества управления: по прямым и по косвенным показателям качества. Получение прямых показателей качества связано с непосредственным исследованием ПП в системе управления, т.е. все рассмотренные показатели, а также процессы вызывающиеся влиянием внешних воздействий. Поэтому прямая оценка качества управления тесно связана с характером и величиной внешних воздействий. Внешние воздействия могут быть разделены на регулярные и случайные. Регулярное воздействие: испытание системы на отработку этих управляющих и возмущающих воздействий (используется обычно набор стандартных типовых функций). Косвенная оценка качества (осуществляется по другим характеристикам, например, частотным или корневым). 5.3. Прямые методы исследования качества САУ. Прямые методы оценки качества состоят из 2-х крупных этапов: 1)построение ПП по исследуемому каналу; 2)исследование ПП и формирование показателей качества и критериев оценки. Построение ПП также возможно двумя путями: 1)экспериментальным или натурным исследованием системы (в условиях эксплуатации); 2)моделированием ПП в системе. Экспериментальное построение ПП применяется в условиях эксплуатации системы (применяют при теоретическом исследовании и математическом моделировании). 5.4. Построение переходного процесса в САУ. Построение ПП в САУ ориентируется на ММ системы. Наиболее распространенной формой описания линейных систем является операторная, поэтому исходные данные для построения ПП представляются обычно структурной схемой регулирования и ПФ входящих в нее звеньев. С использованием этих данных можно получить ПФ системы. Далее построение ПП с их использованием можно проводить 3-мя основными путями: 1) По изображению ПП (изображение по Лапласу). 2) По весовой функции данного канала системы. 3) Прямым решением ДУ (или системы ДУ), описывающим динамику данного канала. 5.4.1. Построение ПП по его изображению. Для этого необходимо задаться видом входного сигнала по данному каналу и найти его изображение по Лапласу (как функции времени), а далее воспользоваться выражением:
где Y(p) - изображение выходного сигнала системы, X(p) - входной сигнал по данному каналу. Получив по формуле (V.1) изображение необходимо подвергнуть обратному преобразованию Лапласа:
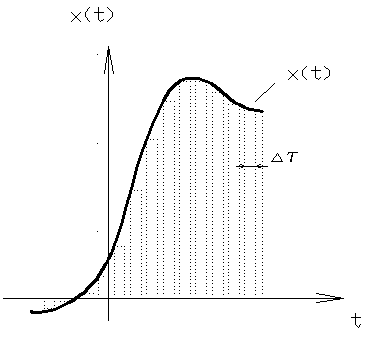
Однако аналитически задача решается сложно (только для невысоких порядков) и в основном для типовых входных воздействий (т.к. для них есть изображение по Лапласу).Целесообразнее воспользоваться таблицами преобразования Лапласа. 5.4.2. Построение ПП по весовой функции канала. Более универсальным способом построения ПП, применимым для входных испытательных воздействий любого сложного вида, представимого в графической или аналитической формах используется подход, основанный на применении интеграла Дюамеля. Сущность этого подхода заключается в том, что реакция ДЗ на входное воздействие произвольного вида может рассматриваться для линейных звеньев как сумма реакций на δ-функцию.
При устремлении интервала квантования времени сумма будет стремиться к площади. В результате получается выражение, которое называют интегралом Дюамеля:
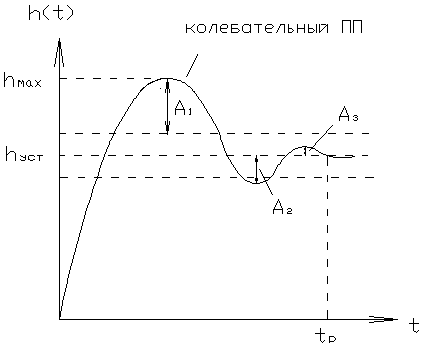
Выражение (5.2) можно получить и из выражения (5.1), так как произведению изображений соответствует функция свертки оригиналов в натуральной области. Таким образом, построение ПП сводится к нахождению весовой функции 5.4.3. Построение ПП прямым решением ДУ. Исходными данными для решения является система ДУ в форме Коши. Для ее решения необходимо задать начальные условия и с помощью начального условия и с помощью известных методов Эйлера и Рунге-Кутта построить переходной процесс. 5.5. Оценка качества САУ по виду ПП. Вид переходного процесса зависит не только от динамических и статических свойств исследования системы, но и от вида входных воздействий, для которых этот процесс получен. Чаще всего переходным процессом называют реакцию системы на единичное ступенчатое воздействие.
1) Переходной процесс с перерегулированием, где
В реальных системах 2) Апериодический переходной процесс.
Самые распространенные – 3% и 15%
5.6. Аналитические методы анализа частных показателей точности работы автоматических систем. 5.6.1. Анализ точности отработки степенных типовых воздействий.
Для анализа точности работы системы надо определить передаточную функцию по каналу ошибки.
Чем больше
Из последних выражений видно, что ошибка тем меньше, чем меньше коэффициент Совокупное значение Свойство преобразования Лапласа:
Используя последнее выражение можно рассмотреть 3 случая соотношения степеней 1) Порядок степенной функции больше порядка астатизма, тогда ошибка отработки реакции данного сигнала неограниченно возрастает и система с ним не справляется 2) Таким образом ошибка будет равна 3) При подачи такого сигнала на вход системы – ошибка отсутствует. Выводы: 1) Если система является статической, то ошибка при подаче ступенчатого воздействия будет постоянной 2) Если система является астатической 1-ого порядка, то при подаче единичного ступенчатого воздействия ошибка стремится к 0. При подаче линейно-нарастающего воздействия равна константе 3) Если система является астатической 2-ого порядка, то при подаче единичного ступенчатого и линейно-нарстающих воздейтсвий ошибка стремится к 0. При параболическом воздействии равна константе 5.6.2. Исследование точности установившихся режимов воспроизведения входных воздействий методов коэффициентов ошибок. Для исследования реакции системы на различные виды воздействий с установленными предельными значениями производных можно разложить функцию
Для нахождения коэффициентов ошибок
Частотные методы оценки обусловлены наличием связи между временными процессами и их Фурье - изображением.
Если задано изображение Фурье входного сигнала, то переходной процесс связан с ним выражением для обратного преобразования Фурье.
Если входным воздействием является ступенчатая функция, у которой изображение:
то найти Y(t) можно по формулам:
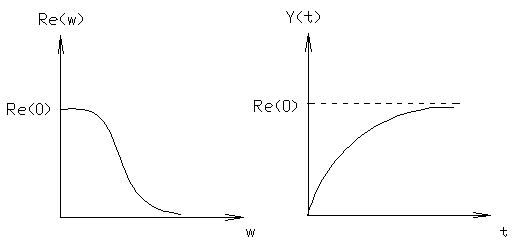
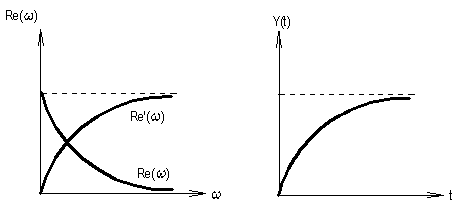
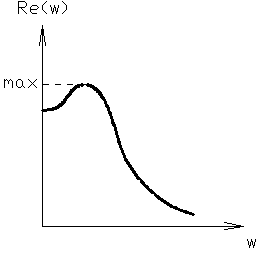
5.8. Качественная и приближенная количественная оценки переходных процессов в линейных системах по их ВЧХ. Связь между ПП и ВЧХ базируется на формуле (5.3) и характеризуется рядом фундаментальных свойств, позволяющих по внешнему виду ВЧХ замкнутой системы и отдельным ее качественным характеристикам, с достаточной для инженерной практики точностью, оценивать вид и отдельные характеристики ПП (в смысле реакции на ступенчатое воздействие). Свойства: 1) линейность связи ВЧХ с Y(t).
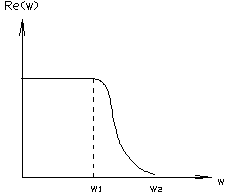
где На этом свойстве базируется так называемый метод трапеций, сущность которого состоит в том, что главный график Re(ω) заменяется кусочно-линейным приближением трапециидального вида. 2) изменение масштабов а) амплитудных (ось ординат). Вытекает все из той же формулы (5.3)
б) аргументных (ось абсцисс)
3) обратность соответствия предельных значений. Это свойство определяется предельной теоремой :
4) оценка экстремумов переходного процесса. а) условие монотонности y(t).
Для монотонности y(t) необходимо и достаточно, чтобы как вещественная характеристика ВЧХ, так и ее производная были монотонными функциями. б) условие ограниченности перерегулирования.
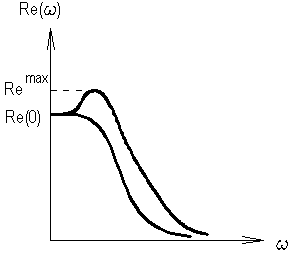
Если ВЧХ является строго убывающей функцией, то перерегулирование ПП не превышает 18%. в) оценка наибольшего перерегулирования. При наличии у вещественной характеристики максимума ПП имеет перерегулирование больше 18%, приближенно определяемое по формуле:
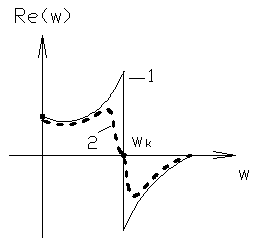
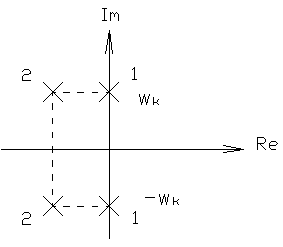
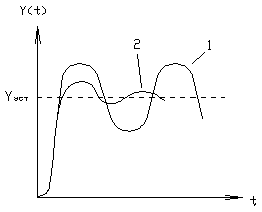
5) колебательность ПП. Оценка этого свойства выводится из того факта, что при наличии в ХП ЗС пары сопряженных мнимых корней вещественная характеристика имеет разрыв второго рода, т.е.приобретает вид, представленный на рисунке (кривая 1). При этом ПП - будет иметь незатухающие колебания во времени. При наличии пары устойчивых, комплексно-сопряженных корней, близких к мнимой оси, вещественная характеристика будет иметь вид представленный на рисунке кривой 2, и чем больше мнимая часть, тем круче характеристика и больше всплески.
Таким образом, ВЧХ содержащая положительные и отрицательные бесконечные выбеги при i-й частоте (так называемая резонансная частота), соответствует колебательным свойствам системы, причем колебательность тем выше (затухание колебаний тем медленнее), чем больше пики этих экстремумов и выше крутизна сопрягающей их части характеристики. 6) условие длительности затухания ПП. а) если ВЧХ имеет строго убывающий характер и близка по виду к трапеции, то время затухания ПП можно определить по формуле:
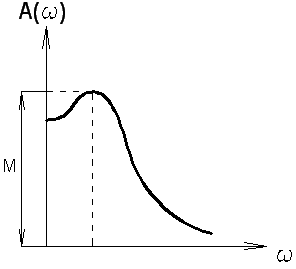
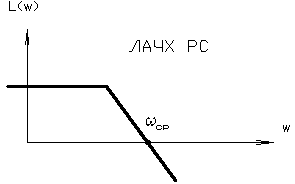
Чем меньше б) при наличии максимума ВЧХ время регулирования определяется по специальным графикам по значениям Rmax и R(0) 5.9. Оценка колебательности ЗС по максимуму АЧХ. При построении и исследовании АЧХ было выявлено, что чем меньше показатель колебательности Для оценки колебательности ЗС без построения ПП можно построить ее АЧХ или ЛАЧХ и по величине амплитудного всплеска характеристики оценить приближенное эквивалентное значение
Соответствие различных показателей показано в таблице (Т-5.1) Таблица 5.1(Т-5.1)
М - максимум АЧХ; m - декремент затухания;
|
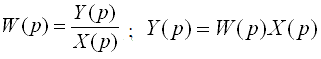 (5.1)
(5.1) 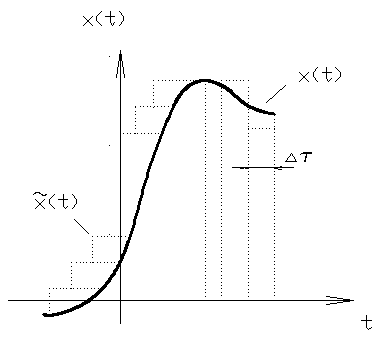
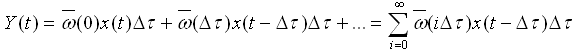
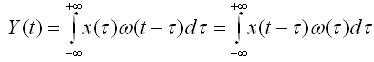 (5.2)
(5.2) 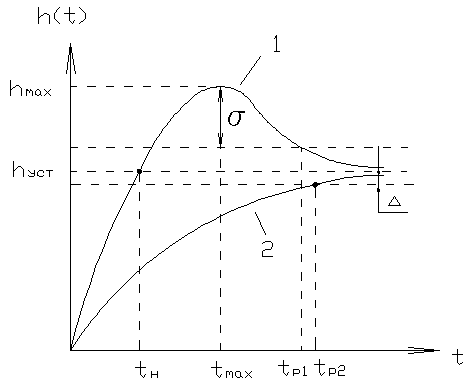
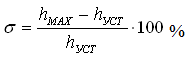
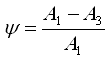 (показатель колебательности)
(показатель колебательности)
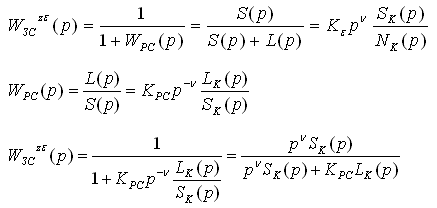
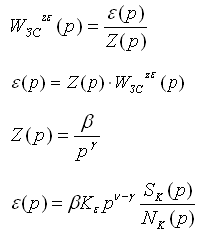
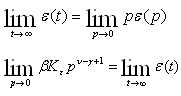
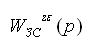 , то есть ее дробно-рациональную часть в ряд Тейлора в окрестности точки
, то есть ее дробно-рациональную часть в ряд Тейлора в окрестности точки 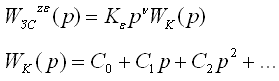
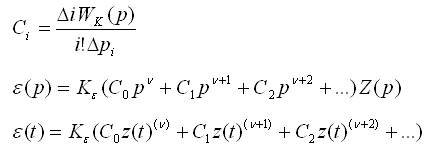
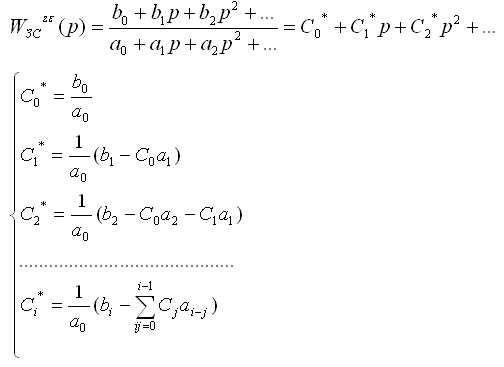
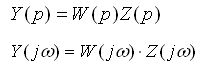
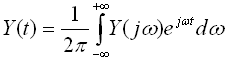
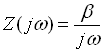
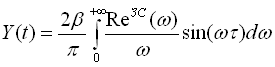 (5.3)
(5.3)